vllbc02Transformer
Transformer
\[ -\log \frac{\exp({\operatorname{sim}\left(\mathbf{h}_i, \mathbf{h}_i^{+}\right) / \tau})}{\sum_{j=1}^N\left(\exp({\operatorname{sim}\left(\mathbf{h}_i, \mathbf{h}_j^{+}\right) / \tau})+\exp({\operatorname{sim}\left(\mathbf{h}_i, \mathbf{h}_j^{-}\right) / \tau}\right))} \]
背景
先从word2vec开始说起，word2vec可以看作是一个预训练模型，但是它有个问题就是它没有办法解决一词多义的问题，比如说bank这个词语，有银行的意思，但在某些语义下，它也有河岸的意思，但对于word2vec来说，它区别不了这两种含义，因为它们尽管上下文环境中出现的单词不同，但是在用语言模型训练的时候，不论什么上下文的句子经过word2vec，都是预测相同的单词bank，而同一个单词占的是同一行的参数空间，这导致两种不同的上下文信息都会编码到相同的word embedding空间里去。
而ELMo就解决了这个问题，它使用了双向的LSTM，具体的可以看ELMo,总之使用RNN作为特征提取器，解决了多义词的问题，但现在来看，RNN的特征提取的能力是远不如本文的Transformer的，为什么要介绍这些东西呢，这就是原因，Transformer出现后，取代了RNN和CNN的地位，成为了最流行的特征提取器，大火的GPT和BERT都与Transformer离不开关系。拿bank为例，RNN在读取整个句子之前不会理解bank的含义，也就是RNN的并行能力比较差，而在Transformer中，token之间会互相交互，也就是所谓的自注意力机制，直观地说，Transformer 的编码器可以被认为是一系列推理步骤（层）。在每一步中，token都会互相看着对方（这是我们需要注意的地方——self-attention），交换信息并尝试在整个句子的上下文中更好地理解对方。这发生在几个层（例如，6 个）中。
在每个解码器层中，前缀标记也通过自注意力机制相互交互。
下面就详细介绍一下。
self-attention
首先介绍一下最主要的self-attention，可以说是self-attention实现了上述的token之间交互的功能。
自注意力是模型的关键组成部分之一。注意 和自注意之间的区别在于，自注意在相同性质的表示之间运行：例如，某个层中的所有编码器状态。
形式上，这种直觉是通过查询键值注意来实现的。self-attention 中的每个输入标记都会收到三种表示，对应于它可以扮演的角色：
- query
- key
- value
进入正题：
作为我们想要翻译的输入语句“The animal didn’t cross the street because
it was too tired”。句子中”it”指的是什么呢？“it”指的是”street”
还是“animal”？对人来说很简单的问题，但是对算法而言并不简单。
当模型处理单词“it”时，self-attention允许将“it”和“animal”联系起来。当模型处理每个位置的词时，self-attention允许模型看到句子的其他位置信息作辅助线索来更好地编码当前词。如果你对RNN熟悉，就能想到RNN的隐状态是如何允许之前的词向量来解释合成当前词的解释向量。Transformer使用self-attention来将相关词的理解编码到当前词中。
下面看一下self-attention是如何计算的：
向量计算
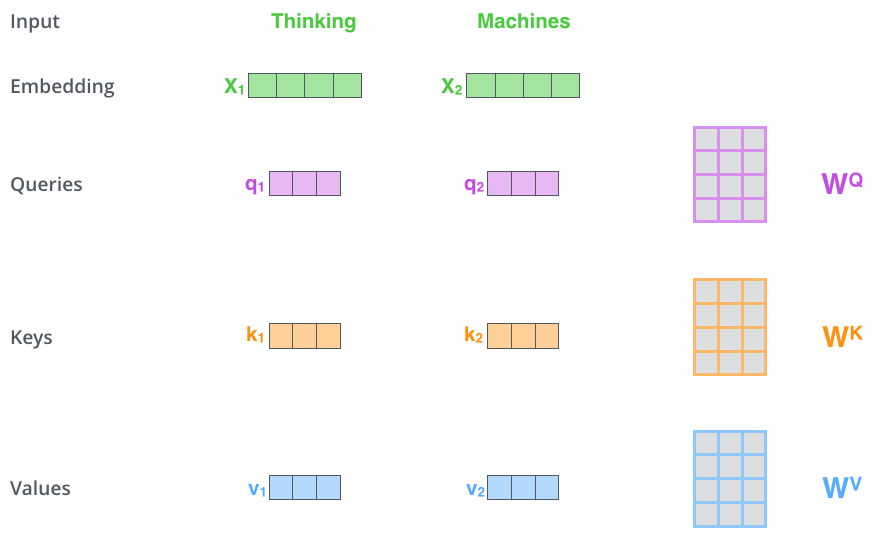
第一步，根据编码器的输入向量，生成三个向量，比如，对每个词向量，生成query-vec,
key-vec,
value-vec，生成方法为分别乘以三个矩阵，这些矩阵在训练过程中需要学习。【注意：不是每个词向量独享3个matrix，而是所有输入共享3个转换矩阵；权重矩阵是基于输入位置的转换矩阵；有个可以尝试的点，如果每个词独享一个转换矩阵，会不会效果更厉害呢？】
注意到这些新向量的维度比输入词向量的维度要小（512–>64），并不是必须要小的，是为了让多头attention的计算更稳定。
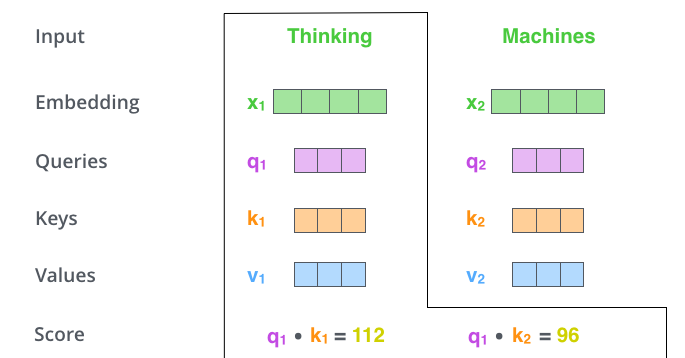
第二步，计算attention就是计算一个分值。对“Thinking
Matchines”这句话，对“Thinking”（pos#1）计算attention
分值。我们需要计算每个词与“Thinking”的评估分，这个分决定着编码“Thinking”时（某个固定位置时），每个输入词需要集中多少关注度。
这个分，通过“Thing”对应query-vector与所有词的key-vec依次做点积得到。所以当我们处理位置#1时，第一个分值是q1和k1的点积，第二个分值是q1和k2的点积。这也就是所谓的注意力得分.
第三步和第四步，除以8(\(=\sqrt{dim_{key}}\))，这样梯度会更稳定。然后加上softmax操作，归一化分值使得全为正数且加和为1。
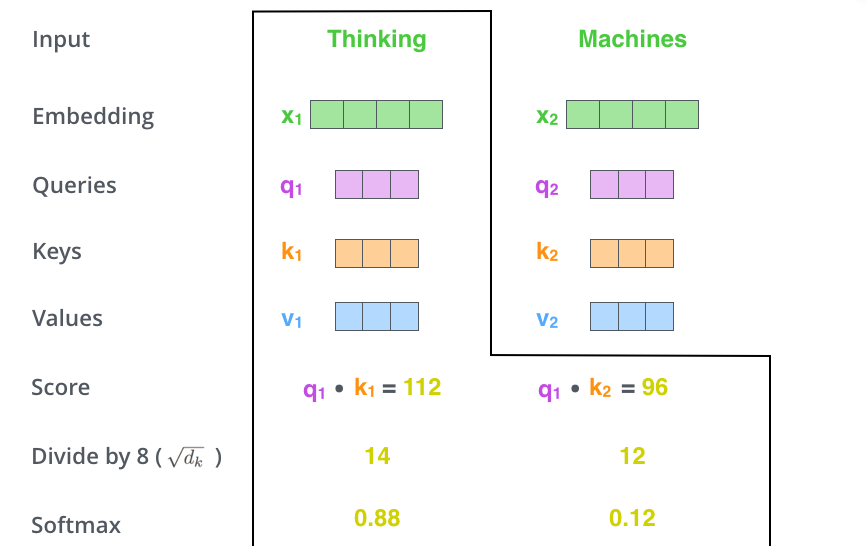
softmax分值决定着在这个位置，每个词的表达程度（关注度）。很明显，这个位置的词应该有最高的归一化分数，但大部分时候总是有助于关注该词的相关的词。
第五步，将softmax分值与value-vec按位相乘。保留关注词的value值，削弱非相关词的value值。
第六步，将所有加权向量加和，产生该位置的self-attention的输出结果。
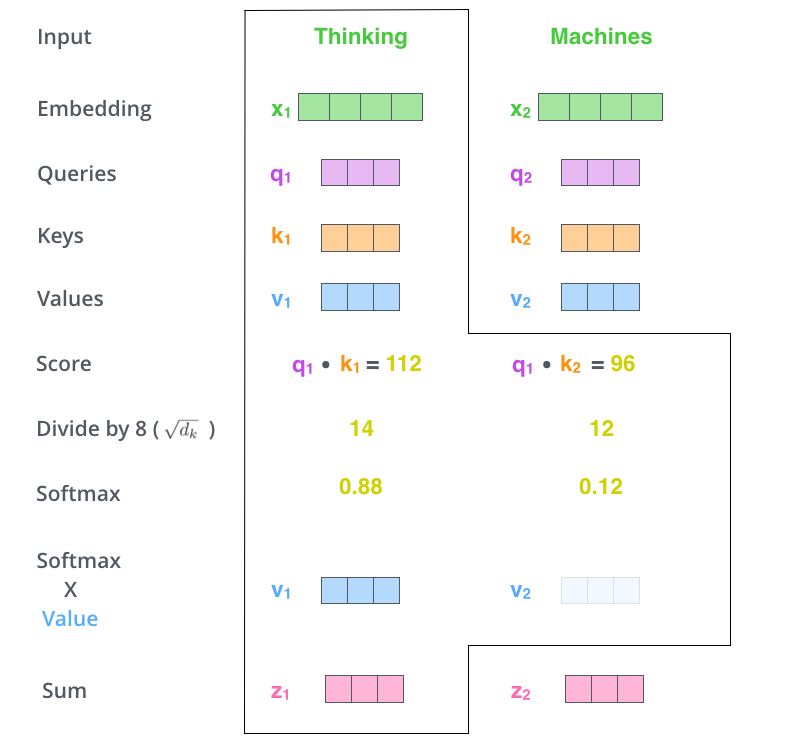
上述就是self-attention的计算过程，生成的向量流入前向网络。在实际应用中，上述计算是以速度更快的矩阵形式进行的。下面我们看下在单词级别的矩阵计算。
矩阵计算
第一步，计算query/key/value matrix，将所有输入词向量合并成输入矩阵\(X\)，并且将其分别乘以权重矩阵\(W^q, W^k,W^v\)
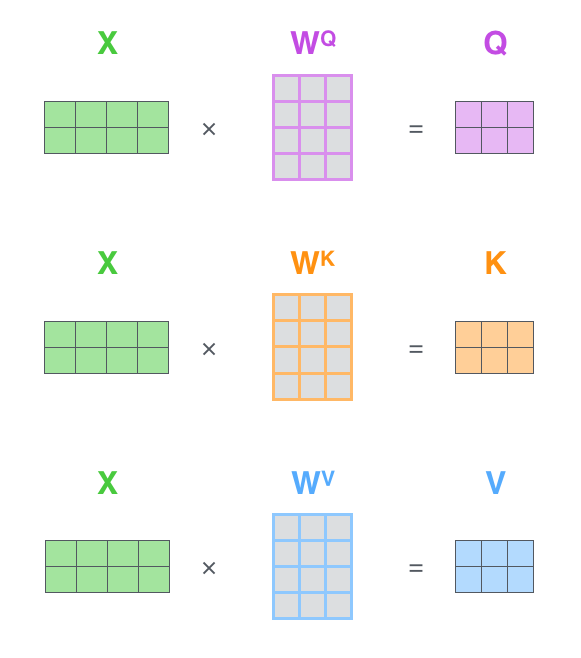最后，鉴于我们使用矩阵处理，将步骤2~6合并成一个计算self-attention层输出的公式。
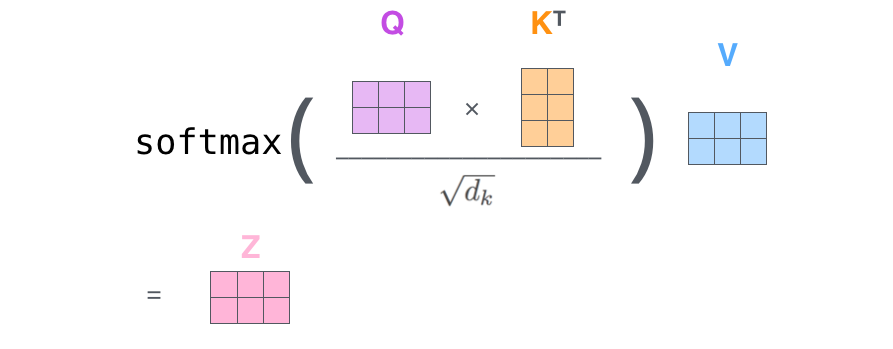
多头注意力机制
论文进一步增加了multi-headed的机制到self-attention上，在如下两个方面提高了attention层的效果：
- 多头机制扩展了模型集中于不同位置的能力。在上面的例子中，z1只包含了其他词的很少信息，仅由实际自己词决定。在其他情况下，比如翻译 “The animal didn’t cross the street because it was too tired”时，我们想知道单词”it”指的是什么。
- 多头机制赋予attention多种子表达方式。像下面的例子所示，在多头下有多组query/key/value-matrix，而非仅仅一组（论文中使用8-heads）。每一组都是随机初始化，经过训练之后，输入向量可以被映射到不同的子表达空间中。
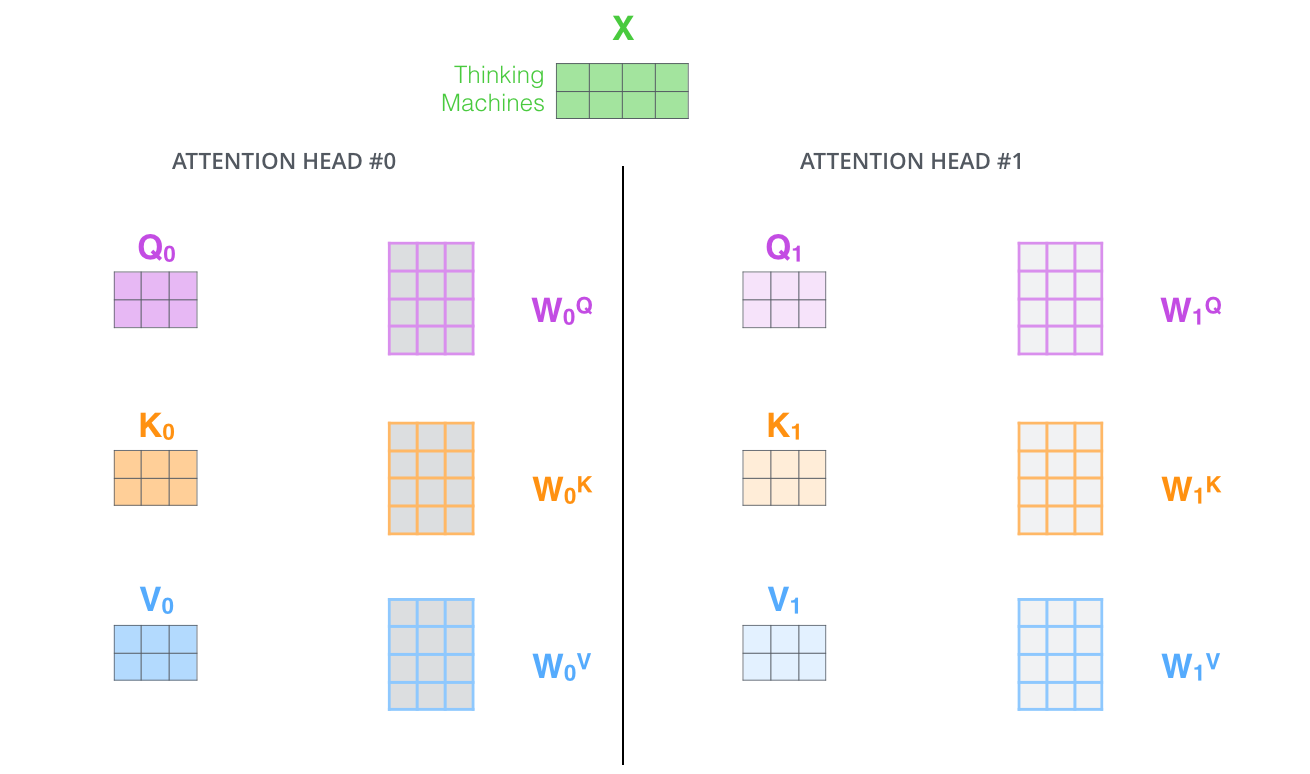如果我们计算multi-headed self-attention的，分别有八组不同的Q/K/V
matrix，我们得到八个不同的矩阵。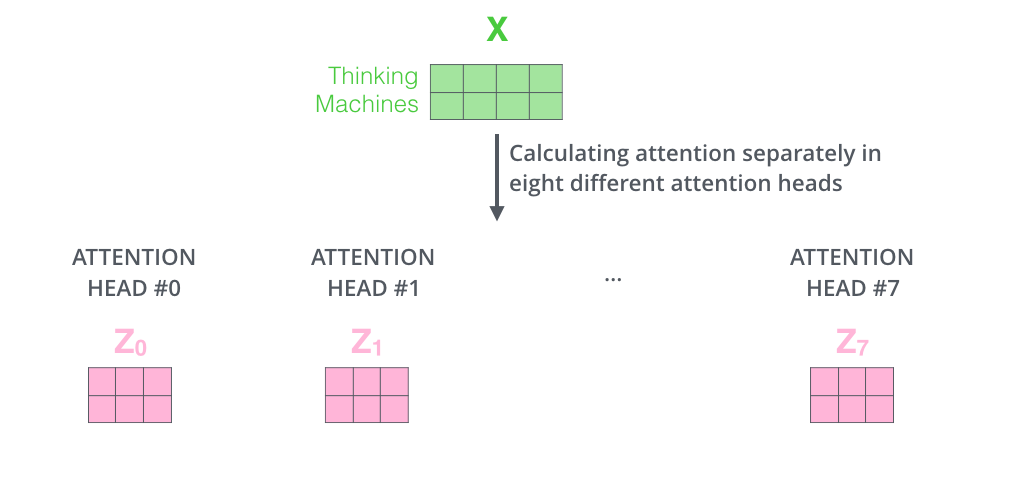 
这会带来点麻烦，前向网络并不能接收八个矩阵，而是希望输入是一个矩阵，所以要有种方式处理下八个矩阵合并成一个矩阵。
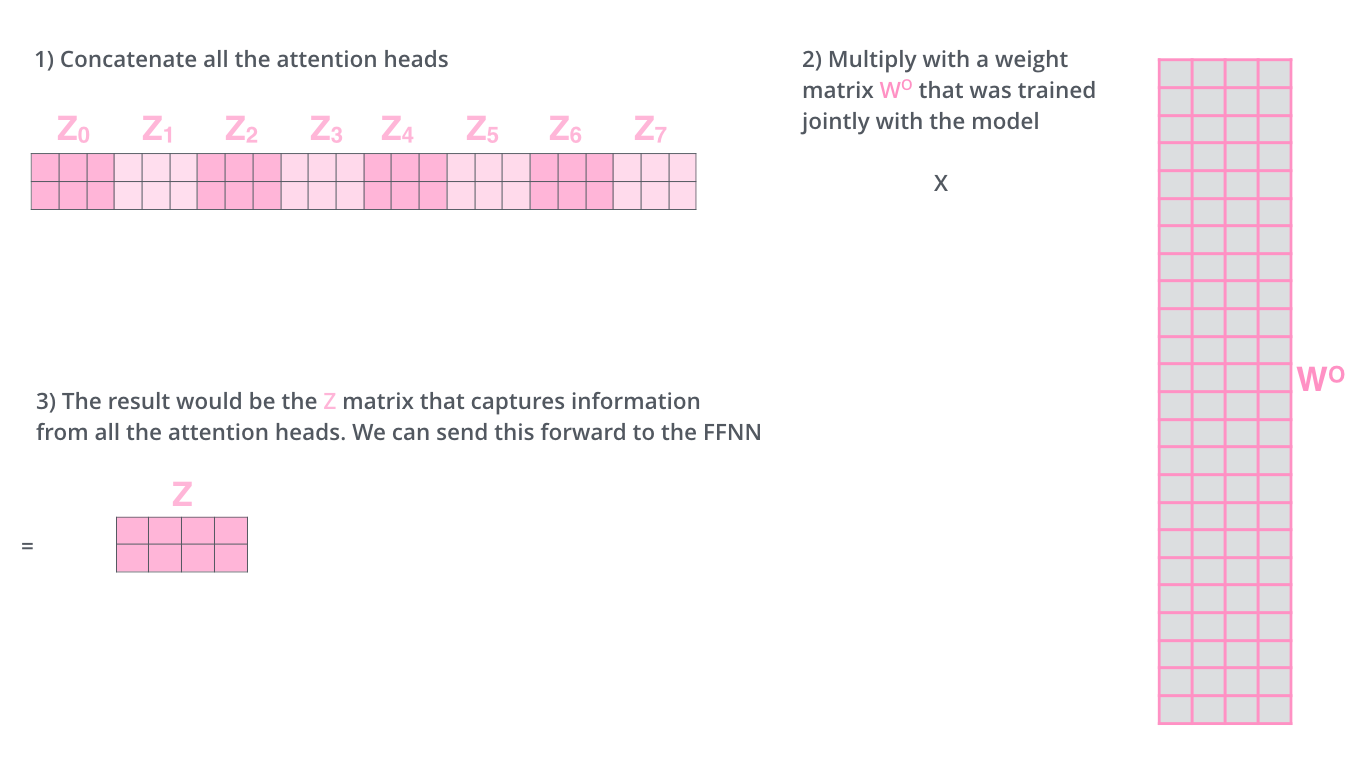
上述就是多头自注意机制的内容，我认为还仅是一部分矩阵，下面尝试着将它们放到一个图上可视化如下。
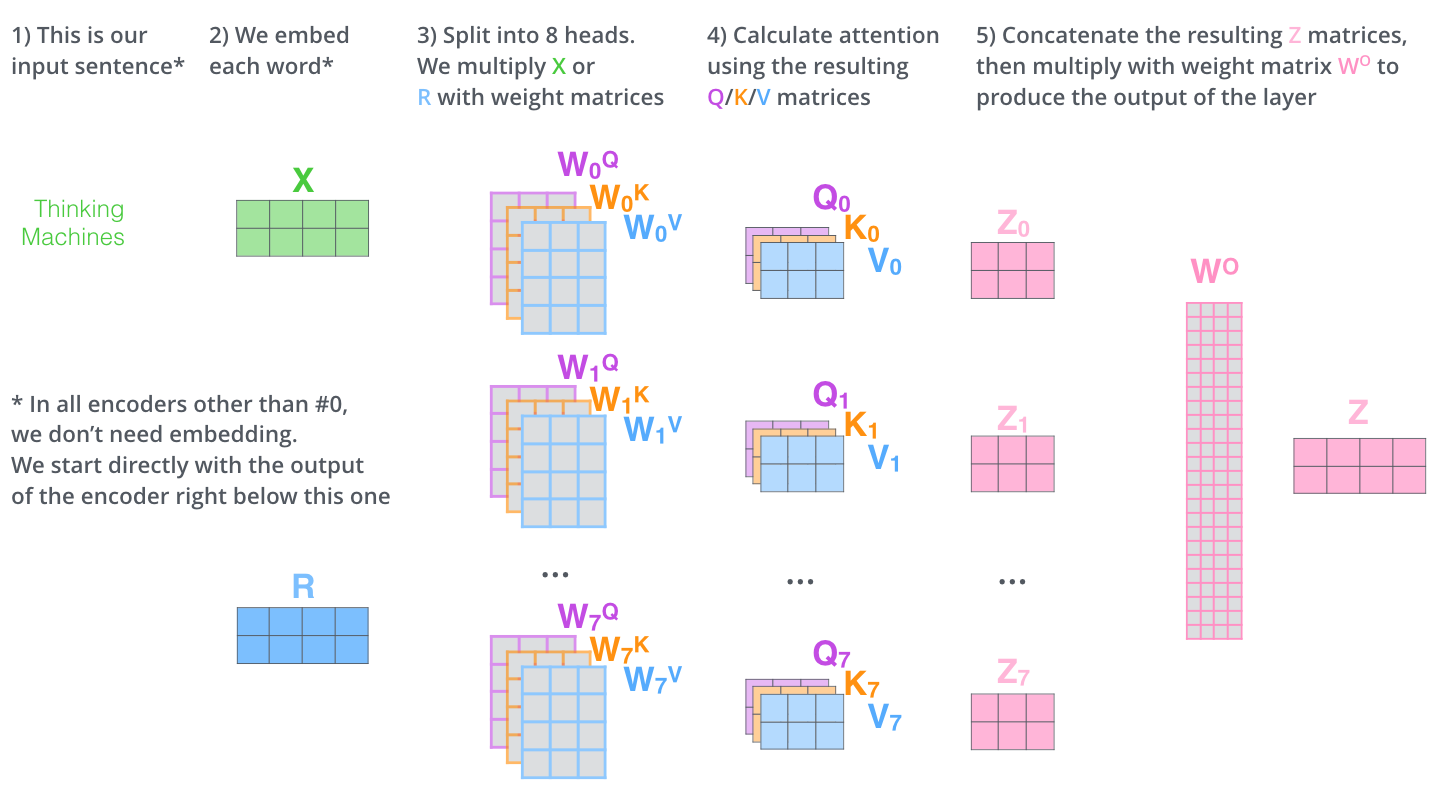#### 代码 下面实现一下多头注意力机制，在原论文中，实现的方法如下： 
也就是对每个W进行多头的设置，即为原维度/head，然后拼接后，再经过\(hd_v\times
d_{model}\)的转换又得到原来的维度，代码的实现不太一样，代码是W还是\(d_{model}\times
d_{model}\)的矩阵然后得到q,k,v之后再进行截断，实现如下。
class MultiHeadedAttention(nn.Module):
def __init__(self, h, d_model, dropout=0.1) -> None:
# h为head，这里为8，d_model为embedding的维度，这里为512
super().__init__()
assert d_model % h == 0
self.d_k = d_model // h # 64
self.h = h
self.Q_Linear = nn.Linear(d_model, d_model)
self.K_Linear = nn.Linear(d_model, d_model)
self.V_Linear = nn.Linear(d_model, d_model)
self.res_Linear = nn.Linear(d_model, d_model)
self.attn = None
self.dropout = nn.Dropout(p=dropout)
def forward(self, query, key, value, mask=None):
if mask is not None:
mask = mask.unsqueeze(1)
batch_size = query.size(0)
query = self.Q_Linear(query).view(batch_size, -1, self.h, self.d_k) # (batch_size, seq_len, h, d_k)即(batch_size, seq_len, 8, 64)
query = query.transpose(1, 2) # (batch_size, h, seq_len, d_k)即(batch_size, 8, seq_len, 64)
key = self.K_Linear(key).view(batch_size, -1, self.h, self.d_k).transpose(1, 2)
value = self.V_Linear(value).view(batch_size, -1, self.h, self.d_k).transpose(1, 2)
x, self.attn = attention(query, key, value, mask=mask, dropout=self.dropout) # x为(batch_size, h, seq_len, d_k)
# attn为(batch_size, h, seq_len1, seq_len2)
x = x.transpose(1, 2).contiguous().view(batch_size, -1, self.h * self.d_k)
# (batch_size, h, seq_len, d_k) -> (batch_size, seq_len, h, d_k) -> (batch_size, seq_len, h * d_k) = (batch_size, seq_len, 512)
return self.res_Linear(x)Masked self-attention
在训练的时候，主要是消除后面的信息对预测的影响，因为decoder输入的是整个句子，也就是我们所谓的参考答案，而实际预测的时候就是预测后面的token，用不到后面的token，如果不mask掉，当前的token将看到“未来”，这不是我们想要的，因此必须要mask掉。
其实decoder里的sequence mask与encoder里的padding mask异曲同工，padding mask其实很简单，就是为了使句子长度一致进行了padding，而为了避免关注padding的位置，进行了mask，具体的做法就是将这些位置的值变成负无穷，这样softmax之后就接近于0了。
而sequence mask思想也差不多：
假设现在解码器的输入”< s > who am i < e
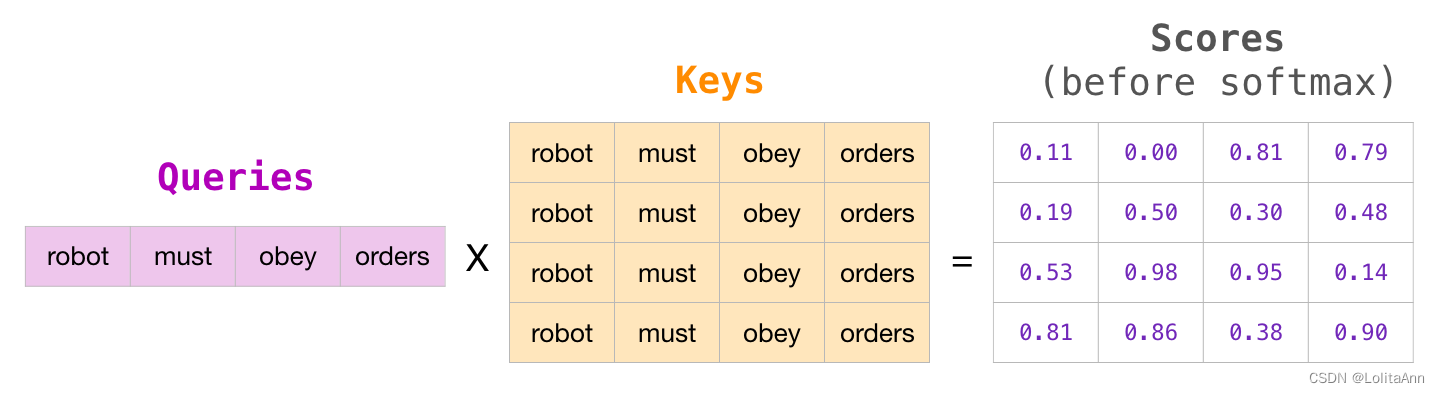
>“在分别乘上一个矩阵进行线性变换后得到了Q、K、V，且Q与K作用后得到了注意力权重矩阵（此时还未进行softmax操作），如图17所示。
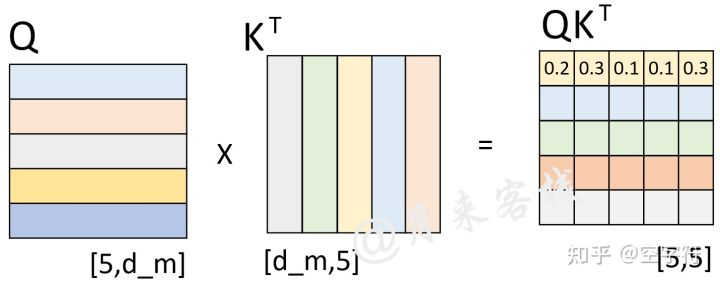
此时已经计算得到了注意力权重矩阵。由第1行的权重向量可知，在解码第1个时刻时应该将20%（严格来说应该是经过softmax后的值）的注意力放到’<
s
>’上，30%的注意力放到’who’上等等。不过此时有一个问题就是，模型在实际的预测过程中只是将当前时刻之前（包括当前时刻）的所有时刻作为输入来预测下一个时刻，也就是说模型在预测时是看不到当前时刻之后的信息。因此，Transformer中的Decoder通过加入注意力掩码机制来解决了这一问题。
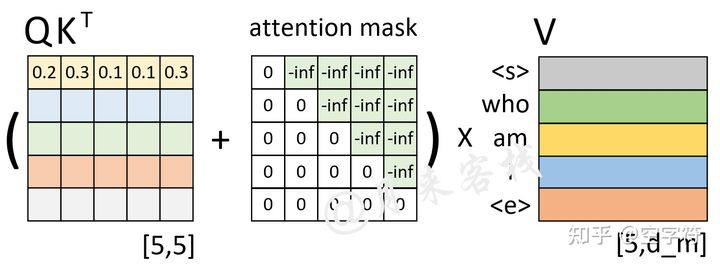当然还要进行softmax等计算。
在网上查了很多资料，说法都很不一样，不过我更倾向于这样的看法。而在预测的时候是用前面的输出结果作为输入的。
几张图帮助理解： 
后面还有padding mask，所有的self attention都要用这个，因为pad的位置没有任何意义。 实践一下加深理解： 首先我们来定义模型：
# 词典数为10， 词向量维度为8
embedding = nn.Embedding(10, 8)
# 定义Transformer，注意一定要改成eval模型，否则每次输出结果不一样
transformer = nn.Transformer(d_model=8, batch_first=True).eval()接下来定义我们的src和tgt：
# Encoder的输入
src = torch.LongTensor([[0, 1, 2, 3, 4]])
# Decoder的输入
tgt = torch.LongTensor([[4, 3, 2, 1, 0]])然后我们将[4]送给Transformer进行预测，模拟推理时的第一步：
transformer(embedding(src), embedding(tgt[:, :1]),
# 这个就是用来生成阶梯式的mask的
tgt_mask=nn.Transformer.generate_square_subsequent_mask(1))tensor([[[ 1.4053, -0.4680, 0.8110, 0.1218, 0.9668, -1.4539, -1.4427,
0.0598]]], grad_fn=<NativeLayerNormBackward0>)然后我们将[4, 3]送给Transformer，模拟推理时的第二步：
transformer(embedding(src), embedding(tgt[:, :2]), tgt_mask=nn.Transformer.generate_square_subsequent_mask(2))tensor([[[ 1.4053, -0.4680, 0.8110, 0.1218, 0.9668, -1.4539, -1.4427,
0.0598],
[ 1.2726, -0.3516, 0.6584, 0.3297, 1.1161, -1.4204, -1.5652,
-0.0396]]], grad_fn=<NativeLayerNormBackward0>)出的第一个向量和上面那个一模一样。
最后我们再将tgt一次性送给transformer，模拟训练过程：
transformer(embedding(src), embedding(tgt), tgt_mask=nn.Transformer.generate_square_subsequent_mask(5))tensor([[[ 1.4053, -0.4680, 0.8110, 0.1218, 0.9668, -1.4539, -1.4427,
0.0598],
[ 1.2726, -0.3516, 0.6584, 0.3297, 1.1161, -1.4204, -1.5652,
-0.0396],
[ 1.4799, -0.3575, 0.8310, 0.1642, 0.8811, -1.3140, -1.5643,
-0.1204],
[ 1.4359, -0.6524, 0.8377, 0.1742, 1.0521, -1.3222, -1.3799,
-0.1454],
[ 1.3465, -0.3771, 0.9107, 0.1636, 0.8627, -1.5061, -1.4732,
0.0729]]], grad_fn=<NativeLayerNormBackward0>)可以看到使用mask后就可以保证前面的结果都是不变的，不然如果没有mask则计算attention时因为计算注意力变化所以结果都会变化，这就是Mask self-attention的意义。 到这里self-attention就介绍完了
代码
def attention(query, key, value, mask=None, dropout=None):
d_k = query.size(-1)
scores = torch.matmul(query, key.transpose(-2, -1)) / math.sqrt(d_k) # 最后两个维度相乘，即为scores，再scale一下。
if mask is not None:
scores = scores.masked_fill(mask == 0, -1e9) # 将mask的位置的scores置为-1e9
# 实际上pad mask的时候，pad也会作为key与其它token对应的k,v计算score，pad mask只是消除pad作为k,v时候的影响。但在最后softmax的时候，将pad的损失值全部置为0
p_attn = F.softmax(scores, dim=-1) # 将scores进行softmax，得到p_attn，这里是在最后一个维度上softmax，因为对每个query的所有key进行softmax
if dropout:
p_attn = dropout(p_attn)
return torch.matmul(p_attn, value), p_attn
class MultiHeadedAttention(nn.Module):
def __init__(self, h, d_model, dropout=0.1) -> None:
# h为head，这里为8，d_model为embedding的维度，这里为512
super().__init__()
assert d_model % h == 0
self.d_k = d_model // h # 64
self.h = h
self.Q_Linear = nn.Linear(d_model, d_model)
self.K_Linear = nn.Linear(d_model, d_model)
self.V_Linear = nn.Linear(d_model, d_model)
self.res_Linear = nn.Linear(d_model, d_model)
self.attn = None
self.dropout = nn.Dropout(p=dropout)
def forward(self, query, key, value, mask=None):
if mask is not None:
mask = mask.unsqueeze(1)
batch_size = query.size(0)
query = self.Q_Linear(query).view(batch_size, -1, self.h, self.d_k) # (batch_size, seq_len, h, d_k)即(batch_size, seq_len, 8, 64)
query = query.transpose(1, 2) # (batch_size, h, seq_len, d_k)即(batch_size, 8, seq_len, 64)
key = self.K_Linear(key).view(batch_size, -1, self.h, self.d_k).transpose(1, 2)
value = self.V_Linear(value).view(batch_size, -1, self.h, self.d_k).transpose(1, 2)
x, self.attn = attention(query, key, value, mask=mask, dropout=self.dropout) # x为(batch_size, h, seq_len, d_k)
# attn为(batch_size, h, seq_len1, seq_len2)
x = x.transpose(1, 2).contiguous().view(batch_size, -1, self.h * self.d_k)
# (batch_size, h, seq_len, d_k) -> (batch_size, seq_len, h, d_k) -> (batch_size, seq_len, h * d_k) = (batch_size, seq_len, 512)
return self.res_Linear(x)模型架构
下面是原始论文中的架构：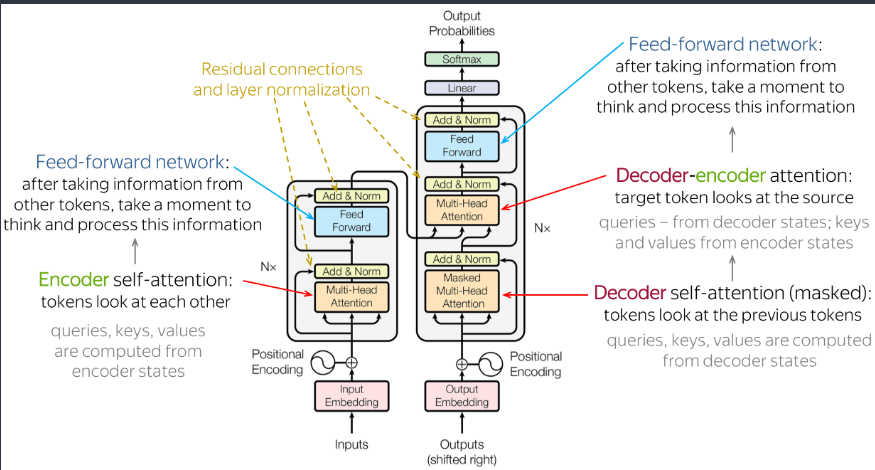 
self-attention上面已经讲的比较详细了，下面说一下其余的部分。
FFN(前馈网络)
除了注意力以外，每一层都有一个前馈网络：两个线性层之间具有ReLU非线性：
\[
FFN(x) = max(0, xW_1+b_1)W_2+b_2
\] 
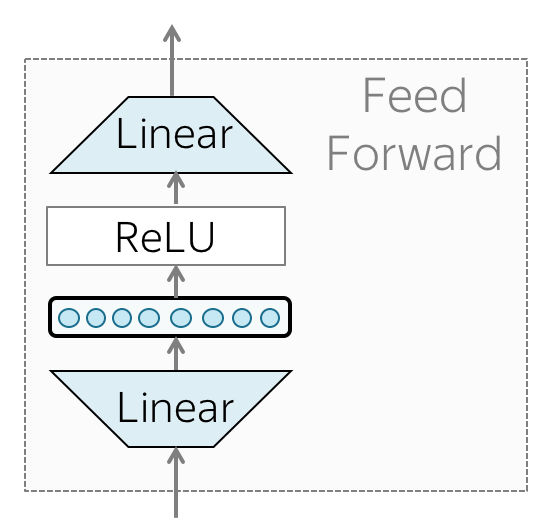
在通过注意力机制查看其他令牌之后，模型使用 FFN 块来处理这些新信息。
class PositionwiseFeedForward(nn.Module):
def __init__(self, d_model, d_ff, dropout=0.1):
super().__init__()
self.w_1 = nn.Linear(d_model, d_ff)
self.w_2 = nn.Linear(d_ff, d_model)
self.dropout = nn.Dropout(p=dropout)
def forward(self, x):
return self.w_2(self.dropout(F.relu(self.w_1(x))))残差连接
残差连接非常简单（将块的输入添加到其输出），但同时也非常有用：它们缓解了通过网络的梯度流并允许堆叠很多层。解决了网络退化的问题。
在 Transformer 中，在每个注意力和 FFN 块之后使用残差连接。在上图中，残差显示为围绕一个块到黄色 “Add & Norm”层的箭头。在“Add & Norm”部分， “Add”部分代表残差连接。
Layer Norm
“Add & Norm”层中的“Norm”部分 表示 Layer Normalization。它批量独立地标准化每个示例的向量表示 - 这样做是为了控制“流”到下一层。层归一化提高了收敛稳定性，有时甚至提高了质量。
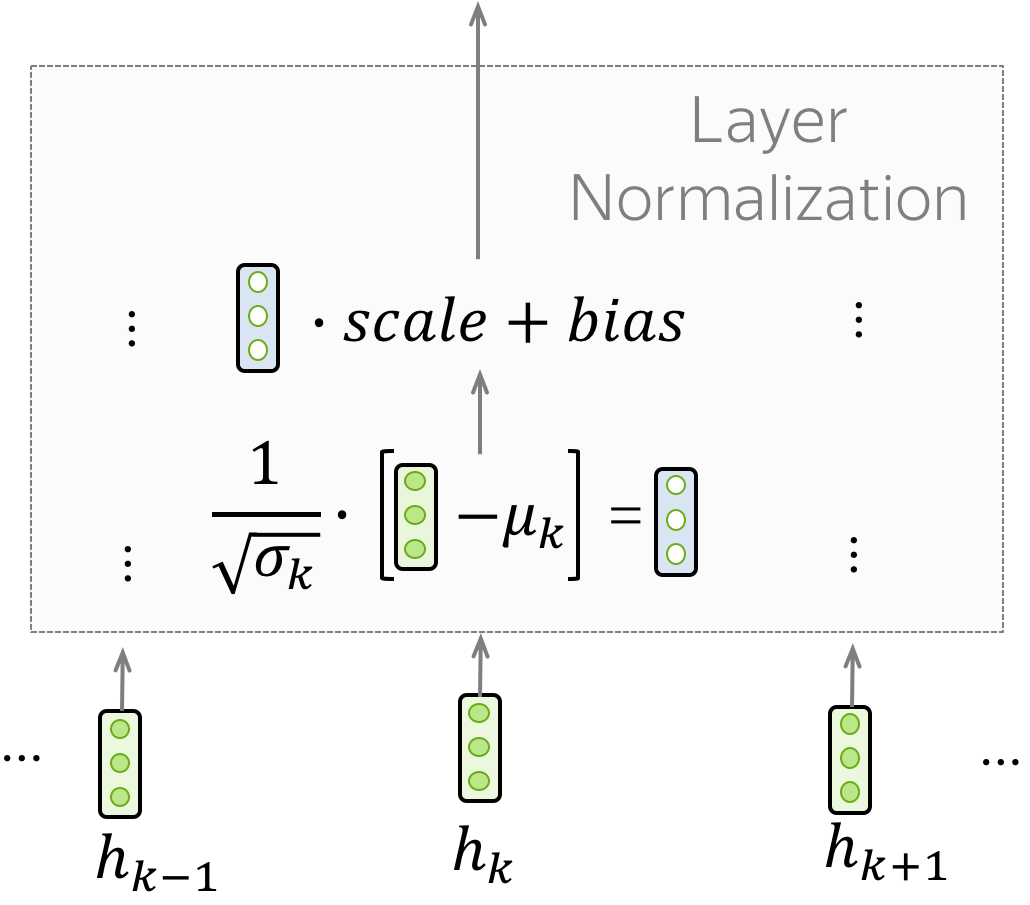这里的scale和bias都是可以训练的参数。
注意Layer Norm与Batch Norm是不同的，这里引用一下沐神的视频：
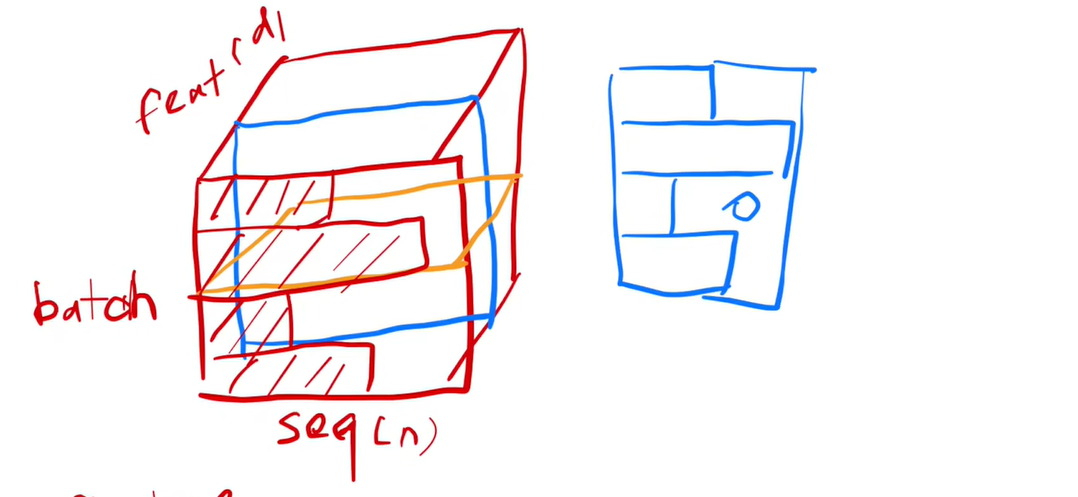
这是Batch Norm的切法，即对每个特征进行norm。
这是Layer norm的切法，即对每个样本进行norm。
为什么用layer norm而不用Batch norm呢？
当你的样本长度变化比较大的时候，使用batch norm计算的均值和方差波动比较大，而且batch norm需要记录全局的均值和方差，当遇到新的测试样本的时候，由于长度的原因，之前的均值方差可能就效果不太好了。
但是如果使用layer norm 的话就没有那么多的问题，因为它是每个样本自己计算均值方差，不需要存在一个全局的均值方差，所以会稳定一点。
class LayerNorm(nn.Module):
def __init__(self, features, eps=1e-6) -> None:
super().__init__()
self.a_2 = nn.Parameter(torch.ones(features))
self.b_2 = nn.Parameter(torch.zeros(features))
self.eps = eps
def forward(self, x):
mean = x.mean(-1, keepdim=True)
std = x.std(-1, keepdim=True)
return self.a_2 * (x - mean) / (std + self.eps) + self.b_2
class SublayerConnection(nn.Module):
def __init__(self, size, dropout) -> None:
super().__init__()
self.norm = LayerNorm(size)
self.dropout = nn.Dropout(p=dropout)
def forward(self, x, sublayer):
return x + self.dropout(sublayer(self.norm(x))) # 这里和论文不同，先norm再扔给sublayer（比如多头注意力、ffd）,理论上是self.norm(x+self.dropout(sublayer(x)))位置编码(position encoding)
(Position Embedding是学习式，而Position Encoding为固定式) 请注意，由于 Transformer 不包含递归或卷积，它不知道输入标记(token)的顺序。因此，我们必须让模型明确地知道标记的位置。为此，我们有两组嵌入：用于标记（我们总是这样做）和用于位置（该模型所需的新嵌入）。那么令牌的输入表示是两个嵌入的总和：令牌和位置。
位置嵌入是可以学习的，但作者发现固定的嵌入不会影响质量。Transformer 中使用的固定位置编码是：
\[ PE_{pos,2i} = sin(\frac{pos}{10000^{\frac{2i}{d_{model}}}}) \]
\[
PE_{pos,2i+1} = cos(\frac{pos}{10000^{\frac{2i}{d_{model}}}})
\] 
可以看到，每个词的维度都是512维，假设句子长度为10，则位置编码的计算如上图所示。
得到位置编码后，将位置编码与词嵌入简单相加即可。 #### 代码
class PositionalEncoding(nn.Module):
def __init__(self, d_model, dropout, max_len=5000) -> None:
super().__init__()
self.dropout = nn.Dropout(p=dropout)
position_embedding = torch.zeros(max_len, d_model)
position = torch.arange(0, max_len).unsqueeze(1)
div_term = torch.exp(torch.arange(0, d_model, 2) * -(math.log(10000.0) / d_model))
position_embedding[:, 0::2] = torch.sin(position * div_term)
position_embedding[:, 1::2] = torch.cos(position * div_term)
position_embedding = position_embedding.unsqueeze(0)
# 增加一维预留batch size的位置，所以后面forward要在第二维上选取序列长度
self.register_buffer('PositionalEncoding', position_embedding)
def forward(self, x):
return self.dropout(x + Variable(self.PositionalEncoding[:, :x.size(1)], requires_grad=False))这里为了计算做了转换。 
### Padding Mask
对于输入序列一般我们都要进行padding补齐，也就是说设定一个统一长度N，在较短的序列后面填充0到长度为N。对于那些补零的数据来说，我们的attention机制不应该把注意力放在这些位置上，所以我们需要进行一些处理。具体的做法是，把这些位置的值加上一个非常大的负数(负无穷)，这样经过softmax后，这些位置的权重就会接近0。Transformer的padding mask实际上是一个张量，每个值都是一个Boolean，值为false的地方就是要进行处理的地方。
label smoothing(标签平滑)
神经网络会促使自身往正确标签和错误标签差值最大的方向学习，在训练数据较少，不足以表征所有的样本特征的情况下，会导致网络过拟合。
label smoothing可以解决上述问题，这是一种正则化策略，主要是通过soft one-hot来加入噪声，减少了真实样本标签的类别在计算损失函数时的权重，最终起到抑制过拟合的效果。
增加label smoothing后真实的概率分布有如下改变：
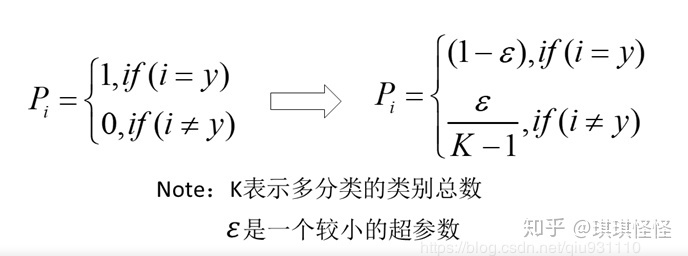
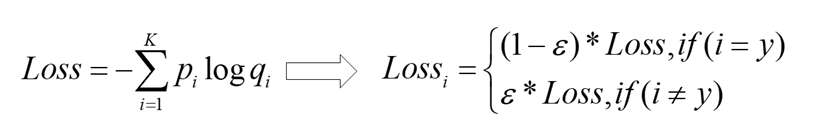
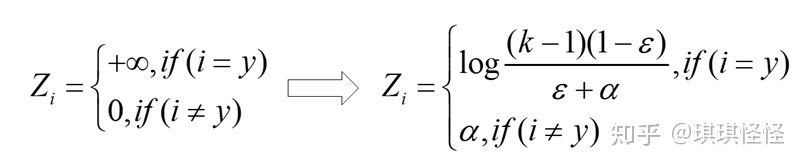
代码
class LabelSmoothing(nn.Module): # [标签平滑](../Deep%20Learning/训练trick/标签平滑.md)损失函数
def __init__(self, size, padding_idx, smoothing=0.0) -> None:
super().__init__()
self.criterion = nn.KLDivLoss(size_average=False)
self.padding_idx = padding_idx
self.confidence = 1.0 - smoothing
self.smoothing = smoothing
self.size = size
self.true_dist = None
def forward(self, x, target):
# x的shape为(batch.size * seq.len, target.vocab.size)
# y的shape是(batch.size * seq.len)
# x=logits，(seq.len, target.vocab.size)
# 每一行，代表一个位置的词
# 类似于：假设seq.len=3, target.vocab.size=5
# x中保存的是log(prob)
#x = tensor([[-20.7233, -1.6094, -0.3567, -2.3026, -20.7233],
#[-20.7233, -1.6094, -0.3567, -2.3026, -20.7233],
#[-20.7233, -1.6094, -0.3567, -2.3026, -20.7233]])
# target 类似于：
# target = tensor([2, 1, 0])，torch.size=(3)
assert x.size(1) == self.size
true_dist = x.data.clone()
# true_dist = tensor([[-20.7233, -1.6094, -0.3567, -2.3026, -20.7233],
#[-20.7233, -1.6094, -0.3567, -2.3026, -20.7233],
#[-20.7233, -1.6094, -0.3567, -2.3026, -20.7233]])
true_dist.fill_(self.smoothing / (self.size - 2))
# true_dist = tensor([[0.1333, 0.1333, 0.1333, 0.1333, 0.1333],
#[0.1333, 0.1333, 0.1333, 0.1333, 0.1333],
#[0.1333, 0.1333, 0.1333, 0.1333, 0.1333]])
# 注意，这里分母target.vocab.size-2是因为
# (1) 最优值 0.6要占一个位置；
# (2) 填充词 <blank> 要被排除在外
# 所以被激活的目标语言词表大小就是self.size-2
true_dist.scatter_(1, target.data.unsqueeze(1), self.confidence)
# target.data.unsqueeze(1) ->
# tensor([[2],
#[1],
#[0]]); shape=torch.Size([3, 1])
# self.confidence = 0.6
# 根据target.data的指示，按照列优先(1)的原则，把0.6这个值
# 填入true_dist: 因为target.data是2,1,0的内容，
# 所以，0.6填入第0行的第2列（列号，行号都是0开始）
# 0.6填入第1行的第1列
# 0.6填入第2行的第0列：
# true_dist = tensor([[0.1333, 0.1333, 0.6000, 0.1333, 0.1333],
#[0.1333, 0.6000, 0.1333, 0.1333, 0.1333],
#[0.6000, 0.1333, 0.1333, 0.1333, 0.1333]])
true_dist[:, self.padding_idx] = 0
# true_dist = tensor([[0.0000, 0.1333, 0.6000, 0.1333, 0.1333],
#[0.0000, 0.6000, 0.1333, 0.1333, 0.1333],
#[0.0000, 0.1333, 0.1333, 0.1333, 0.1333]])
# 设置true_dist这个tensor的第一列的值全为0
# 因为这个是填充词'<blank>'所在的id位置，不应该计入
# 目标词表。需要注意的是，true_dist的每一列，代表目标语言词表
#中的一个词的id
mask = torch.nonzero(target.data == self.padding_idx)
# mask = tensor([[2]]), 也就是说，最后一个词 2,1,0中的0，
# 因为是'<blank>'的id，所以通过上面的一步，把他们找出来
# 如果不加上nonzero，那么mask的shape就是torch.Size([3])
if mask.dim() > 0:
true_dist.index_fill_(0, mask.squeeze(), 0.0)
# 当target reference序列中有0这个'<blank>'的时候，则需要把
# 这一行的值都清空。
# 在一个batch里面的时候，可能两个序列长度不一，所以短的序列需要
# pad '<blank>'来填充，所以会出现类似于(2,1,0)这样的情况
# true_dist = tensor([[0.0000, 0.1333, 0.6000, 0.1333, 0.1333],
# [0.0000, 0.6000, 0.1333, 0.1333, 0.1333],
# [0.0000, 0.0000, 0.0000, 0.0000, 0.0000]])
self.true_dist = true_dist
return self.criterion(x, Variable(true_dist, requires_grad=False))
# 这一步就是调用KL loss来计算
# x = tensor([[-20.7233, -1.6094, -0.3567, -2.3026, -20.7233],
#[-20.7233, -1.6094, -0.3567, -2.3026, -20.7233],
#[-20.7233, -1.6094, -0.3567, -2.3026, -20.7233]])
# true_dist=tensor([[0.0000, 0.1333, 0.6000, 0.1333, 0.1333],
# [0.0000, 0.6000, 0.1333, 0.1333, 0.1333],
# [0.0000, 0.0000, 0.0000, 0.0000, 0.0000]])预测
预测过程与一般seq2seq不同的是，t时刻是将1到t-1时刻所有的预测结果作为序列进行预测，而seq2seq只是使用前一时刻的输出作为当前时刻的输入，这里困扰了我很久，实现了transformer代码后对比李沐老师的代码才理解。
其中seq2seq: 
transformer: 
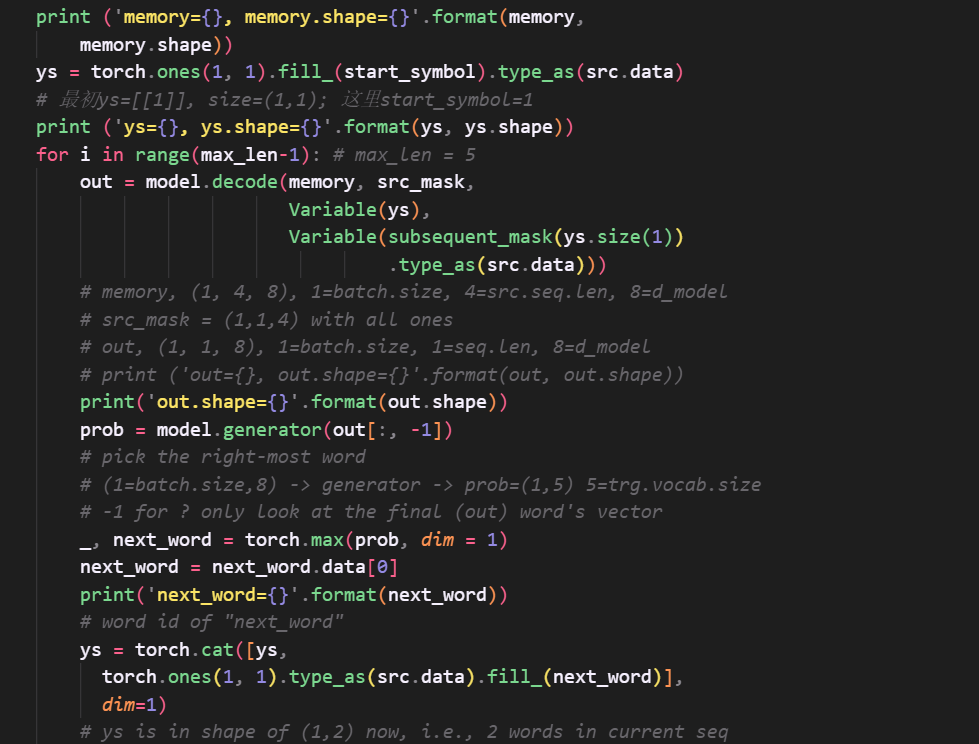注意ys最后与之前的ys使用cat函数合并在一起。 ## 总结
Transformer还有很多的模型细节，以后遇到了再记录一下，在面试中很容易问到这些细节，因此可以参考面经边学习边记录，可以查缺补漏也可以学到新的东西。接下来把代码复现一下可以加深理解，并且提高自己的代码水平和实践能力。
一些问题
Transformer在哪里做了权重共享，为什么可以做权重共享？
Transformer在两个地方进行了权重共享：
（1）Encoder和Decoder间的Embedding层权重共享；
（2）Decoder中Embedding层和FC层权重共享。
对于（1），《Attention is all you need》中Transformer被应用在机器翻译任务中，源语言和目标语言是不一样的，但它们可以共用一张大词表，对于两种语言中共同出现的词（比如：数字，标点等等）可以得到更好的表示，而且对于Encoder和Decoder，嵌入时都只有对应语言的embedding会被激活，因此是可以共用一张词表做权重共享的。
论文中，Transformer词表用了bpe来处理，所以最小的单元是subword。英语和德语同属日耳曼语族，有很多相同的subword，可以共享类似的语义。而像中英这样相差较大的语系，语义共享作用可能不会很大。
但是，共用词表会使得词表数量增大，增加softmax的计算时间，因此实际使用中是否共享可能要根据情况权衡。
对于（2），Embedding层可以说是通过onehot去取到对应的embedding向量，FC层可以说是相反的，通过向量（定义为 x）去得到它可能是某个词的softmax概率，取概率最大（贪婪情况下）的作为预测值。
那哪一个会是概率最大的呢？在FC层的每一行量级相同的前提下，理论上和 x 相同的那一行对应的点积和softmax概率会是最大的。
因此，Embedding层和FC层权重共享，Embedding层中和向量 x 最接近的那一行对应的词，会获得更大的预测概率。实际上，Decoder中的Embedding层和FC层有点像互为逆过程。
通过这样的权重共享可以减少参数的数量，加快收敛。
为什么除以根号d
论文中的解释是：向量的点积结果会很大，将 softmax 函数 push 到梯度很小的区域，scaled 会缓解这种现象。
\[\frac{\partial\mathbf{y}}{\partial\mathbf{x}}=\mathrm{diag}(\mathbf{y})-\mathbf{y}\mathbf{y}^T\] 当\(\mathbf{y} =\)softmax\(( \mathbf{x} )\)时，\(\mathbf{y}\)对\(\mathbf{x}\)的梯度为： 这是一个jacobi矩阵\(^{+}\),表示y的每一个元素对x每一个元素的导数是什么。 展开： \[\frac{\partial\mathbf{y}}{\partial\mathbf{x}}=\begin{bmatrix}y_1&0&\cdots&0\\0&y_2&\cdots&0\\\vdots&\vdots&\ddots&\vdots\\0&0&\cdots&y_d\end{bmatrix}-\begin{bmatrix}y_1^2&y_1y_2&\cdots&y_1y_d\\y_2y_1&y_2^2&\cdots&y_2y_d\\\vdots&\vdots&\ddots&\vdots\\y_dy_1&y_dy_2&\cdots&y_d^2\end{bmatrix}\] 根据前面的讨论，当输入 \(\mathbf{x}\) 的某一个元素较大时，softmax 会把大部分概率分布\(^{+}\)分配给最大的元 素，假设我们的输入数量级很大，那么就将产生一个接近 one-hot 的向量 \[\mathbf{y}\approx[1,0,\cdots,0]^\top \] 此时上面的矩阵变为如下形式 \[\frac{\partial\mathbf{y}}{\partial\mathbf{x}}\approx\begin{bmatrix}1&0&\cdots&0\\0&0&\cdots&0\\\vdots&\vdots&\ddots&\vdots\\0&0&\cdots&0\end{bmatrix}-\begin{bmatrix}1&0&\cdots&0\\0&0&\cdots&0\\\vdots&\vdots&\ddots&\vdots\\0&0&\cdots&0\end{bmatrix}=\mathbf{0}\] 也就是所有的梯度都接近0 除以\(\sqrt{ d }\)后就使x的分布更加平缓，从而防止梯度消失。
from scipy.special import softmax
import numpy as np
def test_gradient(dim, time_steps=50, scale=1.0):
# Assume components of the query and keys are drawn from N(0, 1) independently
q = np.random.randn(dim)
ks = np.random.randn(time_steps, dim)
x = np.sum(q * ks, axis=1) / scale # x.shape = (time_steps,)
y = softmax(x)
grad = np.diag(y) - np.outer(y, y)# softmax gradient(dy/dx)
return np.max(np.abs(grad)) # the maximum component of gradients
NUMBER_OF_EXPERIMENTS = 5
# results of 5 random runs without scaling
print([test_gradient(100) for _ in range(NUMBER_OF_EXPERIMENTS)])
print([test_gradient(1000) for _ in range(NUMBER_OF_EXPERIMENTS)])
# results of 5 random runs with scaling
print([test_gradient(100, scale=np.sqrt(100)) for _ in range(NUMBER_OF_EXPERIMENTS)])
print([test_gradient(1000, scale=np.sqrt(1000)) for _ in range(NUMBER_OF_EXPERIMENTS)])输出可看到下面的梯度比上面的梯度更大。
这时又有一个问题，为什么多分类的softmax+交叉熵不需要除以东西呢？这是因为交叉熵中有一个log，log_softmax的梯度和刚才算出来的不同，就算输入的某一个x过大也不会梯度消失。所以就又可以推断出softmax+MSE会导致梯度消失，因为MSE中没有Log，这是为什么分类任务不使用MSE损失函数的原因之一。 ### 为什么 Transformer 需要进行 Multi-head Attention 实验证明多头是必要的，8/16个头都可以取得更好的效果，但是超过16个反而效果不好。每个头关注的信息不同，但是头之间的差异随着层数增加而减少。并且不是所有头都有用，有工作尝试剪枝，可以得到更好的表现。
论文中提到模型分为多个头，形成多个子空间，每个头关注不同方面的信息。
那为什么每个头的维度要降呢? 一言蔽之的话，大概是：在不增加时间复杂度的情况下，同时，借鉴CNN多核的思想，在更低的维度，在多个独立的特征空间，更容易学习到更丰富的特征信息。 ### 为什么 Transformer 的 Embedding 最后要乘dmodel 具体的原因是，如果使用 Xavier 初始化，Embedding 的方差为 1/d_model，当d_model非常大时，矩阵中的每一个值都会减小。通过乘一个 dmodel 可以将方差恢复到1。
因为Position Encoding是通过三角函数算出来的，值域为[-1, 1]。所以当加上 Position Encoding 时，需要放大 embedding 的数值，否则规模不一致相加后会丢失信息。
因为 Bert 使用的是学习式的Embedding，所以 Bert 这里就不需要放大。 # 参考