SVD奇异值分解

参考：https://www.cnblogs.com/pinard/p/6251584.html

特征值与特征向量

首先回顾特征值与特征向量$Ax=\lambda x$

$\lambda$ 是矩阵A的一个特征值，x是矩阵A的特征值$\lambda$对应的特征向量。

求出特征值与特征向量可以将矩阵A进行特征分解。如果求出了A的n个特征值，以及这n个特征值所对应的特征向量$w_1,w_2,\dots ,w_n$，如果这n个特征向量线性无关，则矩阵A就可以用下式进行表示：

$$A=W\sum W^{-1}$$

其中W为这n个特征向量所张成的$n\times n$维矩阵，$\sum$为这n个特征值为主对角线的矩阵。

我们一般会把n个特征向量标准化，即$w_i^T{w}_i=1$，此时W的n个特征向量为标准正交基，满足$W^{T}W=I$，即$W^T=W^{-1}$，也就是说W为酉矩阵。

这样特征分解表达式可以写为$A=W\sum W^T$

特征分解要求A必须为方阵，如果行列不相同则使用SVD进行分解。

SVD

假设A为一个$m\times n$的矩阵，那么定义A的SVD为：

$$A=U\sum V^T$$

其中U是一个$m\times n$的矩阵，$\sum$是一个$m\times n$的矩阵，除了主对角线上的元素全为0，主对角线上的每个元素成为奇异值，V是一个$n\times n$的矩阵，U和V都是酉矩阵。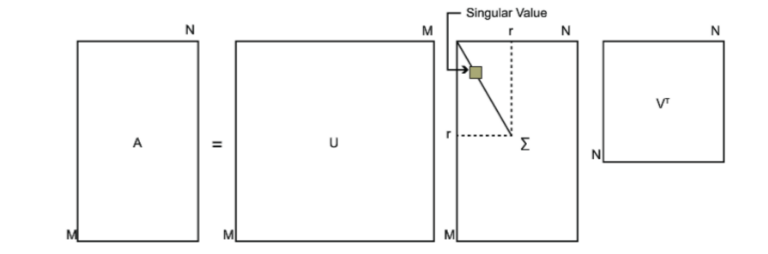

先得到$m\times m$的方阵$A{A}^T$,然后进行特征值分解，$(A{A}^T)u_i={\lambda }_i{u}_i$ 将$A{A}^T$的所有特征向量张成一个$m\times m$的矩阵U，就是SVD公式里面的U矩阵了。

后得到$n\times n$的方阵$A^{T}A$,然后进行特征值分解，$(A^{T}A)v_i={\lambda }_i{v}_i$ 将$A^{T}A$的所有特征向量张成一个$n\times n$的矩阵V，就是SVD公式里面的V矩阵了。

特征值和奇异值满足以下关系${\sigma }_i=\sqrt{{\lambda }_i}$，意思就是我们可以通过求$A^{T}A$的特征值取平方根来求奇异值。