rwkv

2024-09-04 约 1125 字预计阅读 3 分钟次阅读

线性Transformer

\[V_i'=\frac{\sum_{j=1}^N sim(Q_i,K_j)V_j}{\sum_{j=1}^N sim(Q_i,K_j)}\] 注意下标i。其中

\[sim(Q_{i},K_{j})=\phi(Q_{i},K_{j})\]

此时有：

\[V_{i}^{\prime}=\frac{\phi(Q_{i})\sum_{j=1}^{i}\phi(K_{j})^{T}V_{j}}{\phi(Q_{i})\sum_{j=1}^{i}\phi(K_{j})^{T}}\]

注意可以将\(\phi(Q_{i})\)提出来。

原始Transformer的计算复杂度随序列长N呈二次方增长，这是因为attention的计算包含两层for循环，外层是对于每一个Query，我们需要计算它对应token的新表征；内层for循环是为了计算每一个Query对应的新表征，需要让该Query与每一个Key进行计算。所以外层是 for q in Queries，内层是 for k in Keys。Queries数量和Keys数量都是N，所以复杂度是 O(N^2) 。而Linear Transformer，它只有外层for q in Queries这个循环了。因为求和项的计算与i无关，所以所有的 Qi 可以共享求和项的值。换言之，求和项的值可以只计算一次，然后存在内存中供所有 Qi 去使用。所以Linear Transformer的计算复杂度是O(N) 。

Attention Free Transformer

\[V_i'=\sigma(Q_i)\odot\frac{\sum_{j-1}^iexp(K_j+w_{i,j})\odot V_j}{\sum_{j=1}^iexp(K_j+w_{i,j})}\] 其中σ是sigmoid函数\(^{+};\odot\)是逐元素相乘 (element-wise product); wi,j是待训练的参数。 AFT采用的形式和上面的Linear Transformer不一样。首先是attention score, Linear Transformer仍然是同Transformer一样，为每一个Value赋予一个weight。而AFT会为每个 dimension\(^{+}\)赋予weight。换言之，在Linear Transformer中，同一个Value中不同dimension的weight是一致的；而AFT同一Value中不同dimension的weight不同(\(w_{i,j}\))。此外，attention score的计算也变得格外简单，用K去加一个可训练的bias\(^{+}\)。Q的用法很像一个gate。可以很容易仿照公式(5)把AFT也写成递归形式，这样容易看出，AFT也可以像Linear Transformer,在inference阶段复用前面时刻的计算结果，表现如RNN形式，从而相比于 Transformer变得更加高效。

RWKV

RWKV的特点如下：

改造AFT，通过Liner Transformer变换将self-attention复杂度由O(N^2)降为 O(N) 。
保留AFT简单的“attention”形式和Sequential Decoding，具有RNN表现形式。

Time-Mixing

def time_mixing(x, last_x, last_num, last_den, decay, bonus, mix_k, mix_v, mix_r, Wk, Wv, Wr, Wout):
    k = Wk @ ( x * mix_k + last_x * (1 - mix_k) )
    v = Wv @ ( x * mix_v + last_x * (1 - mix_v) )
    r = Wr @ ( x * mix_r + last_x * (1 - mix_r) )

    wkv = (last_num + exp(bonus + k) * v) /      \
          (last_den + exp(bonus + k))
    rwkv = sigmoid(r) * wkv

    num = exp(-exp(decay)) * last_num + exp(k) * v
    den = exp(-exp(decay)) * last_den + exp(k)

    return Wout @ rwkv, (x,num,den)

Channel-Mixing

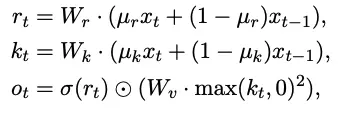
def channel_mixing(x, last_x, mix_k, mix_r, Wk, Wr, Wv):
    k = Wk @ ( x * mix_k + last_x * (1 - mix_k) )
    r = Wr @ ( x * mix_r + last_x * (1 - mix_r) )
    vk = Wv @ np.maximum(k, 0)**2
    return sigmoid(r) * vk, x

参考

How the RWKV language model works | The Good Minima (johanwind.github.io)

目录