vllbc02rope
证明
核心思想就是找到一个转换，可以通过点积操作将位置信息注入，即： \[<f_q\left(x_m,m\right),f_k\left(x_n,n\right)>=g\left(x_m,x_n,m-n\right)\] 而通过复数的一些性质，找到了满足上述操作的转换：
\[\begin{aligned} &f_{q}\left(\boldsymbol{x}_{m},m\right)=\left(\boldsymbol{W}_{q}\boldsymbol{x}_{m}\right)e^{im\theta} \\ &f_{k}\left(\boldsymbol{x}_{n},n\right)=\left(\boldsymbol{W}_{k}\boldsymbol{x}_{n}\right)e^{in\theta} \\ &g\left(\boldsymbol{x}_{m},\boldsymbol{x}_{n},m-n\right)=\mathrm{Re}\left[\left(\boldsymbol{W}_{q}\boldsymbol{x}_{m}\right)\left(\boldsymbol{W}_{k}\boldsymbol{x}_{n}\right)^{*}e^{i(m-n)\theta}\right] \end{aligned}\] 可以发现g函数中存在相对位置信息。 欧拉公式：\(e^{ix}=\cos x+i\sin x\)
\[\begin{aligned}&\text{基于上面面1点结论,可知}\\&f_{q}\left(x_{m},m\right)=\left(W_{q}x_{m}\right)e^{im\theta}=q_{m}e^{im\theta}\\&\text{然后将}q_{m\text{表示成复数形式（torch.view\_as\_complex）,可得}}\\&q_{m}=\left[q_{m}^{(1)},q_{m}^{(2)}\right]=\left[q_{m}^{(1)}+iq_{m}^{(2)}\right]\\&\text{从而有}\\&f_{q}\left(x_{m},m\right)=q_{m}e^{im\theta}=\left[q_{m}^{(1)}+iq_{m}^{(2)}\right]e^{im\theta}\\&\text{基于欧拉公式,可知}f_{q}\left(x_{m},m\right)_{\text{即是两个复数相乘}}\\&f_{q}\left(x_{m},m\right)=q_{m}e^{im\theta}=\left(q_{m}^{(1)}+iq_{m}^{(2)}\right)*\left(\cos(m\theta)+i\sin(m\theta)\right)\end{aligned}\]
根据复数的计算，可得：
\[\begin{aligned}q_{m}e^{im\theta}=\left(q_{m}^{(1)}+iq_{m}^{(2)}\right)*(\cos(m\theta)+i\sin(m\theta))\\=\left(q_{m}^{(1)}\cos(m\theta) -q_{m}^{(2)}\sin(m\theta)\right)+i\left(q_{m}^{(2)}\cos(m\theta)+q_{m}^{(1)}\sin(m\theta)\right)\end{aligned}\]
再将结果写成向量的形式，即：
\[q_{m}e^{im\theta}=\left[q_{m}^{(1)}\cos(m\theta)-q_{m}^{(2)}\sin(m\theta),q_{m}^{(2)}\cos(m\theta)+q_{m}^{(1)}\sin(m\theta)\right]\]
即是query向量乘了一个旋转矩阵：
\[\begin{gathered} f_{q}\left(x_{m},m\right)=\left(W_{q}x_{m}\right)e^{im\theta}=q_{m}e^{im\theta} \\ =\left|q_{m}^{(1)}\cos(m\theta)-q_{m}^{(2)}\sin(m\theta),q_{m}^{(2)}\cos(m\theta)+q_{m}^{(1)}\sin(m\theta)\right| \\ =\left(\begin{array}{cc}{\cos(m\theta)}&{-\sin(m\theta)}\\{\sin(m\theta)}&{\cos(m\theta)}\end{array}\right)\left(\begin{array}{c}{q_{m}^{(1)}}\\{q_{m}^{(2)}}\end{array}\right) \end{gathered}\]
后续的证明看一文通透位置编码：从标准位置编码、旋转位置编码RoPE到ALiBi、LLaMA 2 Long(含NTK-aware简介)-CSDN博客
将二维推广，有：
\[\boldsymbol{R}_{\Theta,m}^{d}=\underbrace{\left(\begin{array}{ccccccc}{\cos m\theta_{0}}&{-\sin m\theta_{0}}&{0}&{0}&{\cdots}&{0}&{0}\\{\sin m\theta_{0}}&{\cos m\theta_{0}}&{0}&{0}&{\cdots}&{0}&{0}\\{0}&{0}&{\cos m\theta_{1}}&{-\sin m\theta_{1}}&{\cdots}&{0}&{0}\\{0}&{0}&{\sin m\theta_{1}}&{\cos m\theta_{1}}&{\cdots}&{0}&{0}\\{\vdots}&{\vdots}&{\vdots}&{\vdots}&{\ddots}&{\vdots}&{\vdots}\\{0}&{0}&{0}&{0}&{\cdots}&{\cos m\theta_{d/2-1}}&{-\sin m\theta_{d/2-1}}\\{0}&{0}&{0}&{0}&{0}&{\cdots}&{\sin m\theta_{d/2-1}}&{\cos m\theta_{d/2-1}}\end{array}\right)}\]
则计算旋转编码，即有：
\[\begin{bmatrix}\cos m\theta_0&-\sin m\theta_0&0&0&\cdots&0&0\\\sin m\theta_0&\cos m\theta_0&0&0&\cdots&0&0\\0&0&\cos m\theta_1&-\sin m\theta_1&\cdots&0&0\\0&0&\sin m\theta_1&\cos m\theta_1&\cdots&0&0\\\vdots&\vdots&\vdots&\vdots&\ddots&\vdots&\vdots\\0&0&0&0&\cdots&\cos m\theta_{d/2-1}&-\sin m\theta_{d/2-1}\\0&0&0&0&\cdots&\sin m\theta_{d/2-1}&\cos m\theta_{d/2-1}\end{bmatrix}\begin{bmatrix}q_0\\q_1\\q_2\\q_3\\\vdots\\q_{d-2}\\q_{d-1}\end{bmatrix}\]
由于矩阵太稀疏，会造成浪费，因此计算时是这么做的： \[\begin{bmatrix}q_0\\q_1\\q_2\\q_3\\\vdots\\q_{d-2}\\q_{d-1}\end{bmatrix}\otimes\begin{bmatrix}\cos m\theta_0\\\cos m\theta_0\\\cos m\theta_1\\\cos m\theta_1\\\vdots\\\cos m\theta_{d/2-1}\\\cos m\theta_{d/2-1}\end{bmatrix}+\begin{bmatrix}-q_1\\q_0\\-q_3\\q_2\\\vdots\\-q_{d-1}\\q_{d-2}\end{bmatrix}\otimes\begin{bmatrix}\sin m\theta_0\\\sin m\theta_0\\\sin m\theta_1\\\sin m\theta_1\\\vdots\\\sin m\theta_{d/2-1}\\\sin m\theta_{d/2-1}\end{bmatrix}\] 此外，角度的计算方式如下：
\[\theta_j=10000^{-2j/d},j\in[1,2,\dots,d/2]\]
代码
llama实现
llama实现比较简单，但是一开始很不容易理解，实现如下：
def precompute_freqs_cis(dim: int, end: int, theta: float = 10000.0):
"""
Precompute the frequency tensor for complex exponentials (cis) with given dimensions.
This function calculates a frequency tensor with complex exponentials using the given dimension 'dim'
and the end index 'end'. The 'theta' parameter scales the frequencies.
The returned tensor contains complex values in complex64 data type.
Args:
dim (int): Dimension of the frequency tensor.
end (int): End index for precomputing frequencies.
theta (float, optional): Scaling factor for frequency computation. Defaults to 10000.0.
Returns:
torch.Tensor: Precomputed frequency tensor with complex exponentials.
"""
# dim = 128
# end = 4096
# torch.arange(0, dim, 2) [0, 2, 4, 6, 8, 10,..., 124, 126] 共64个
# torch.arange(0, dim, 2)[: (dim // 2)] 保证是64个
freqs = 1.0 / (theta ** (torch.arange(0, dim, 2)[: (dim // 2)].float() / dim)) # rope中的角度
# freqs = [1/10000.0^(0/128), 1/10000.0^(2/128), 1/10000.0^(4/128), ..., 1/10000.0^(126/128)]
t = torch.arange(end, device=freqs.device) # postition idx
# t = [0, 1, 2, ..., 4095]
freqs = torch.outer(t, freqs).float() # type: ignore
# freqs 得到 freqs和t的笛卡尔积，维度为（4096，64）
# freqs = [[0, 0, 0,..., 0],
# [1/10000.0^(0/128), 1/10000.0^(2/128), 1/10000.0^(4/128), ..., 1/10000.0^(126/128)],
# [2/10000.0^(0/128), 2/10000.0^(2/128), 2/10000.0^(4/128), ..., 2/10000.0^(126/128)],
# ...,
# [4095/10000.0^(0/128), 4095/10000.0^(2/128), 4095/10000.0^(4/128), ..., 4095/10000.0^(126/128)]]
freqs_cis = torch.polar(torch.ones_like(freqs), freqs) # complex64
# freqs_cis的维度为(4096,64)，相当于半径为1，角度为freqs的极坐标的复数表示，如公式6所示。
return freqs_cis
def reshape_for_broadcast(freqs_cis: torch.Tensor, x: torch.Tensor): # 将除了position和dim其他的维度变为1
"""
Reshape frequency tensor for broadcasting it with another tensor.
This function reshapes the frequency tensor to have the same shape as the target tensor 'x'
for the purpose of broadcasting the frequency tensor during element-wise operations.
Args:
freqs_cis (torch.Tensor): Frequency tensor to be reshaped.
x (torch.Tensor): Target tensor for broadcasting compatibility.
Returns:
torch.Tensor: Reshaped frequency tensor.
Raises:
AssertionError: If the frequency tensor doesn't match the expected shape.
AssertionError: If the target tensor 'x' doesn't have the expected number of dimensions.
"""
# freqs_cis.shape = [1024, 64]
# x.shape = [2, 1024, 32, 64]
ndim = x.ndim
assert 0 <= 1 < ndim
assert freqs_cis.shape == (x.shape[1], x.shape[-1])
# 将freqs_cis.shape变为[1, 1024, 1, 64]
shape = [d if i == 1 or i == ndim - 1 else 1 for i, d in enumerate(x.shape)]
return freqs_cis.view(*shape)
def apply_rotary_emb(
xq: torch.Tensor,
xk: torch.Tensor,
freqs_cis: torch.Tensor,
):
"""
Apply rotary embeddings to input tensors using the given frequency tensor.
This function applies rotary embeddings to the given query 'xq' and key 'xk' tensors using the provided
frequency tensor 'freqs_cis'. The input tensors are reshaped as complex numbers, and the frequency tensor
is reshaped for broadcasting compatibility. The resulting tensors contain rotary embeddings and are
returned as real tensors.
Args:
xq (torch.Tensor): Query tensor to apply rotary embeddings.
xk (torch.Tensor): Key tensor to apply rotary embeddings.
freqs_cis (torch.Tensor): Precomputed frequency tensor for complex exponentials.
Returns:
Tuple[torch.Tensor, torch.Tensor]: Tuple of modified query tensor and key tensor with rotary embeddings.
"""
# 将xq和xk的最后一个维度进行复数运算，得到新的xq和xk
# 为了进行复数运算，需要将xq和xk的最后一个维度展开为2维
# 例如，xq的形状为[2, seq_len, 32, 128], reshape后为[2, seq_len, 32 , 64, 2]
# view_as_complex函数可以将张量中的最后一维的两个元素作为实部和虚部合成一个复数xq的形状变为[2, seq_len, 32, 64]
xq_ = torch.view_as_complex(xq.float().reshape(*xq.shape[:-1], -1, 2))
xk_ = torch.view_as_complex(xk.float().reshape(*xk.shape[:-1], -1, 2))
# 将freqs_cis广播到xq和xk的最后一个维度
freqs_cis = reshape_for_broadcast(freqs_cis, xq_)
# freqs_cis.shape = [1, 1024, 1, 64]
# view_as_real和view_as_complex相反，可以将张量中最后一维的复数拆出实部和虚部
# (xq_ * freqs_cis).shape = [2, seq_len, 32 , 64]
# torch.view_as_real(xq_ * freqs_cis).shape = [2, seq_len, 32 , 64, 2]
# flatten(3)将张量展平为[2, seq_len, 32 , 128]，3代表从的第3个维度开始展平
xq_out = torch.view_as_real(xq_ * freqs_cis).flatten(3)
xk_out = torch.view_as_real(xk_ * freqs_cis).flatten(3)
return xq_out.type_as(xq), xk_out.type_as(xk)代码的实现是根据下面这个公式来的：
\[\begin{aligned}q_{m}e^{im\theta}=\left(q_{m}^{(1)}+iq_{m}^{(2)}\right)*(\cos(m\theta)+i\sin(m\theta))\\=\left(q_{m}^{(1)}\cos(m\theta) -q_{m}^{(2)}\sin(m\theta)\right)+i\left(q_{m}^{(2)}\cos(m\theta)+q_{m}^{(1)}\sin(m\theta)\right)\end{aligned}\] 因为对于query的dim维度，两两组合再变成复数形式，并和对应的旋转矩阵相乘，然后再转换成向量形式。这样就完成了转换。
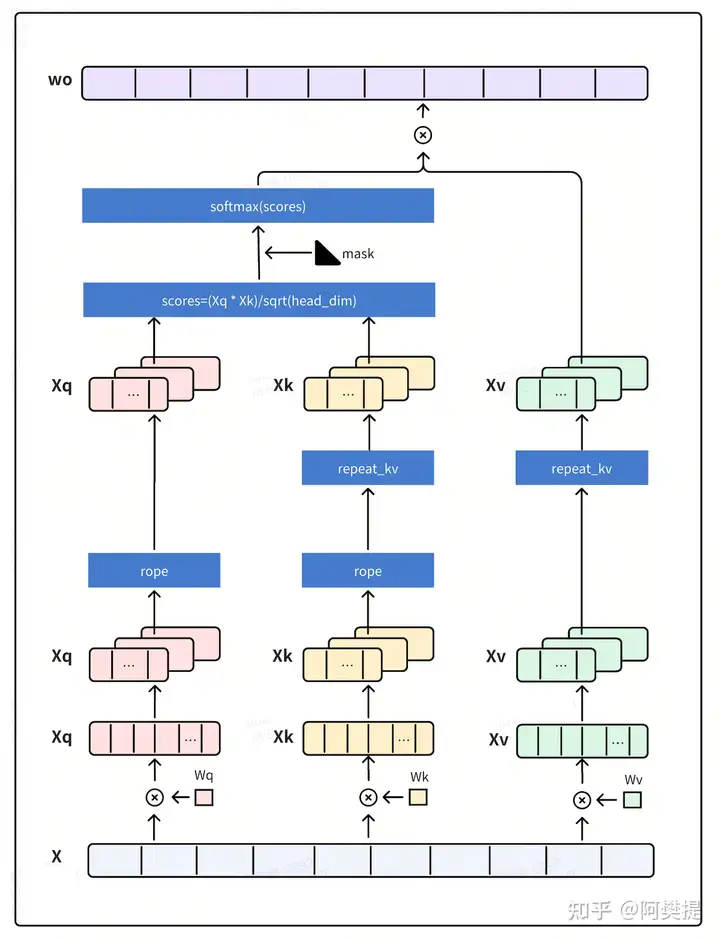
另一种实现
另一种实现(transformers)利用了下面这个式子：
\[ \begin{bmatrix}q_0\\q_1\\q_2\\q_3\\\vdots\\q_{d-2}\\q_{d-1}\end{bmatrix}\otimes\begin{bmatrix}\cos m\theta_0\\\cos m\theta_0\\\cos m\theta_1\\\cos m\theta_1\\\vdots\\\cos m\theta_{d/2-1}\\\cos m\theta_{d/2-1}\end{bmatrix}+\begin{bmatrix}-q_1\\q_0\\-q_3\\q_2\\\vdots\\-q_{d-1}\\q_{d-2}\end{bmatrix}\otimes\begin{bmatrix}\sin m\theta_0\\\sin m\theta_0\\\sin m\theta_1\\\sin m\theta_1\\\vdots\\\sin m\theta_{d/2-1}\\\sin m\theta_{d/2-1}\end{bmatrix} \]
class LlamaRotaryEmbedding(torch.nn.Module):
def __init__(self, dim, max_position_embeddings=2048, base=10000, device=None):
super().__init__()
inv_freq = 1.0 / (base ** (torch.arange(0, dim, 2).float().to(device) / dim))
self.register_buffer("inv_freq", inv_freq)
# Build here to make `torch.jit.trace` work.
self.max_seq_len_cached = max_position_embeddings
t = torch.arange(self.max_seq_len_cached, device=self.inv_freq.device,
dtype=self.inv_freq.dtype)
freqs = torch.einsum("i,j->ij", t, self.inv_freq)
# Different from paper, but it uses a different permutation
# in order to obtain the same calculation
emb = torch.cat((freqs, freqs), dim=-1)
dtype = torch.get_default_dtype()
self.register_buffer("cos_cached", emb.cos()[None, None, :, :].to(dtype), persistent=False)
self.register_buffer("sin_cached", emb.sin()[None, None, :, :].to(dtype), persistent=False)
def forward(self, x, seq_len=None):
# x: [bs, num_attention_heads, seq_len, head_size]
# This `if` block is unlikely to be run after we build sin/cos in `__init__`.
# Keep the logic here just in case.
if seq_len > self.max_seq_len_cached:
self.max_seq_len_cached = seq_len
t = torch.arange(self.max_seq_len_cached, device=x.device, dtype=self.inv_freq.dtype)
freqs = torch.einsum("i,j->ij", t, self.inv_freq)
# Different from paper, but it uses a different permutation
# in order to obtain the same calculation
emb = torch.cat((freqs, freqs), dim=-1).to(x.device)
self.register_buffer("cos_cached", emb.cos()[None, None, :, :].to(x.dtype),
persistent=False)
self.register_buffer("sin_cached", emb.sin()[None, None, :, :].to(x.dtype),
persistent=False)
return (
self.cos_cached[:, :, :seq_len, ...].to(dtype=x.dtype),
self.sin_cached[:, :, :seq_len, ...].to(dtype=x.dtype),
)
def rotate_half(x):
"""Rotates half the hidden dims of the input."""
x1 = x[..., : x.shape[-1] // 2]
x2 = x[..., x.shape[-1] // 2 :]
return torch.cat((-x2, x1), dim=-1)
def apply_rotary_pos_emb(q, k, cos, sin, position_ids):
# The first two dimensions of cos and sin are always 1, so we can `squeeze` them.
cos = cos.squeeze(1).squeeze(0) # [seq_len, dim]
sin = sin.squeeze(1).squeeze(0) # [seq_len, dim]
cos = cos[position_ids].unsqueeze(1) # [bs, 1, seq_len, dim]
sin = sin[position_ids].unsqueeze(1) # [bs, 1, seq_len, dim]
q_embed = (q * cos) + (rotate_half(q) * sin)
k_embed = (k * cos) + (rotate_half(k) * sin)
return q_embed, k_embed相对于llama的版本比较容易理解。
Long-term decay of RoPE
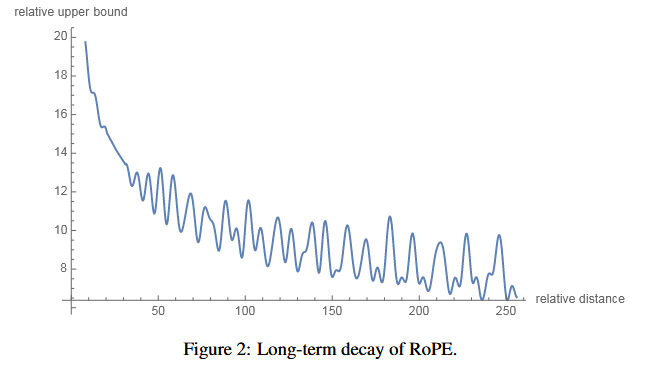公式不看了，结论就是RoPE有长距离衰减的特性，相对距离越远的token之间的关注度也会降低，表现为attention
score减小，这是个很好的特性。”This property coincides with the intuition
that a pair of tokens with a long relative distance should have less
connection.“ # 参考 一文通透位置编码：从标准位置编码、旋转位置编码RoPE到ALiBi、LLaMA
2 Long(含NTK-aware简介)-CSDN博客