vllbc02PPMI
PMI
点互信息 对于两个单词之间的PMI来说，可以这样计算：
\[ PMI(w,c) = \log \frac{p(w,c)}{p(w)p(c)} = \log \frac{N(w,c) |w,c|}{N(w)N(c)} \] ## MI 在概率论和信息论中，两个随机变量的互信息（Mutual Information，简称MI）或转移信息（transinformation）是变量间相互依赖性的量度。不同于相关系数，互信息并不局限于实值随机变量，它更加一般且决定着联合分布 p(X,Y) 和分解的边缘分布的乘积 p(X)p(Y) 的相似程度。互信息(Mutual Information)是度量两个事件集合之间的相关性(mutual dependence)。互信息最常用的单位是bit。
定义
正式地，两个离散随机变量 X 和 Y 的互信息可以定义为： 其中 p(x,y) 是 X
和 Y 的联合概率分布函数，而p(x)和p(y)分别是 X 和 Y 的边缘概率分布函数。
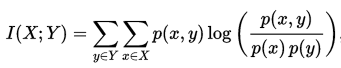
在结果上互信息与信息增益是一样的，下面是详细的推导。 
应用到文本特征选择：
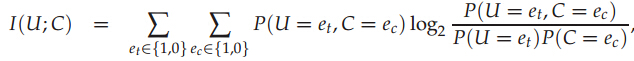U、C都是二值随机变量，当文档包含词项t时，U的取值为1，否则0；当文档属于类别c时，C的取值1，否则0。简单的理解就是对于文本来说，每一个token就是它的特征，取值只有有或者没有，也就是0或者1，互信息常用于文本特征的选择，也就
是选择有价值的token。在贝叶斯文本分类中用到了，特此记录。
\[ I_k = \sum_{\tilde{y}=0}^1 \bigg(p(X = k | Y = \tilde{y})p(Y = \tilde{y}) \log\frac{p(X = k | Y = \tilde{y})}{p(X=k)} + (1-p(X = k | Y = \tilde{y}))p(Y = \tilde{y}) \log\frac{1 - p(X = k | Y = \tilde{y})}{1 - p(X = k)}\bigg), \]
公式如上。\(I_k\)意味着单词k与Y之间的互信息。
示例代码如下：
def calculateMI(dtm_ham_train, dtm_spam_train):
ham_sums = np.sum(dtm_ham_train, axis=0)
ham_probs = ham_sums / np.sum(ham_sums)
spam_sums = np.sum(dtm_spam_train, axis=0)
spam_probs = spam_sums / np.sum(spam_sums)
all_sums = ham_sums + spam_sums
all_probs = all_sums / sum(all_sums)
mi = []
for i in range(len(all_probs)):
if all_probs[i] == 0 or np.isnan(all_probs[i]):
mi.append(0)
else:
mi.append(.5 * ham_probs[i] * np.log(ham_probs[i] / all_probs[i]) +
.5 * (1 - ham_probs[i]) * np.log((1 - ham_probs[i])/(1 - all_probs[i])) +
.5 * spam_probs[i] * np.log(spam_probs[i] / all_probs[i]) +
.5 * (1 - spam_probs[i]) * np.log((1 - spam_probs[i])/(1 - all_probs[i])))
mi = np.array(mi)
mi = np.where(np.isnan(mi), 0, mi)
return miPPMI
