rope
证明
核心思想就是找到一个转换,可以通过点积操作将位置信息注入,即: \[<f_q\left(x_m,m\right),f_k\left(x_n,n\right)>=g\left(x_m,x_n,m-n\right)\] 而通过复数的一些性质,找到了满足上述操作的转换:
\[\begin{aligned} &f_{q}\left(\boldsymbol{x}_{m},m\right)=\left(\boldsymbol{W}_{q}\boldsymbol{x}_{m}\right)e^{im\theta} \\ &f_{k}\left(\boldsymbol{x}_{n},n\right)=\left(\boldsymbol{W}_{k}\boldsymbol{x}_{n}\right)e^{in\theta} \\ &g\left(\boldsymbol{x}_{m},\boldsymbol{x}_{n},m-n\right)=\mathrm{Re}\left[\left(\boldsymbol{W}_{q}\boldsymbol{x}_{m}\right)\left(\boldsymbol{W}_{k}\boldsymbol{x}_{n}\right)^{*}e^{i(m-n)\theta}\right] \end{aligned}\] 可以发现g函数中存在相对位置信息。 欧拉公式:\(e^{ix}=\cos x+i\sin x\)
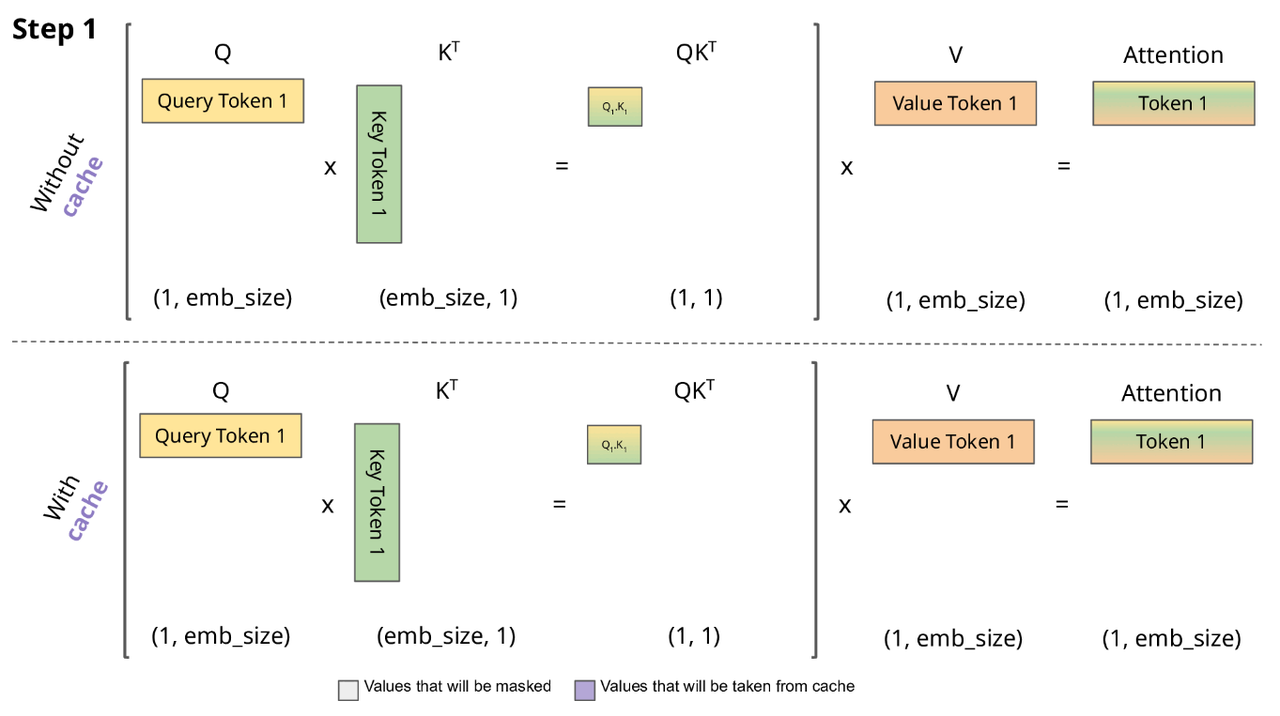
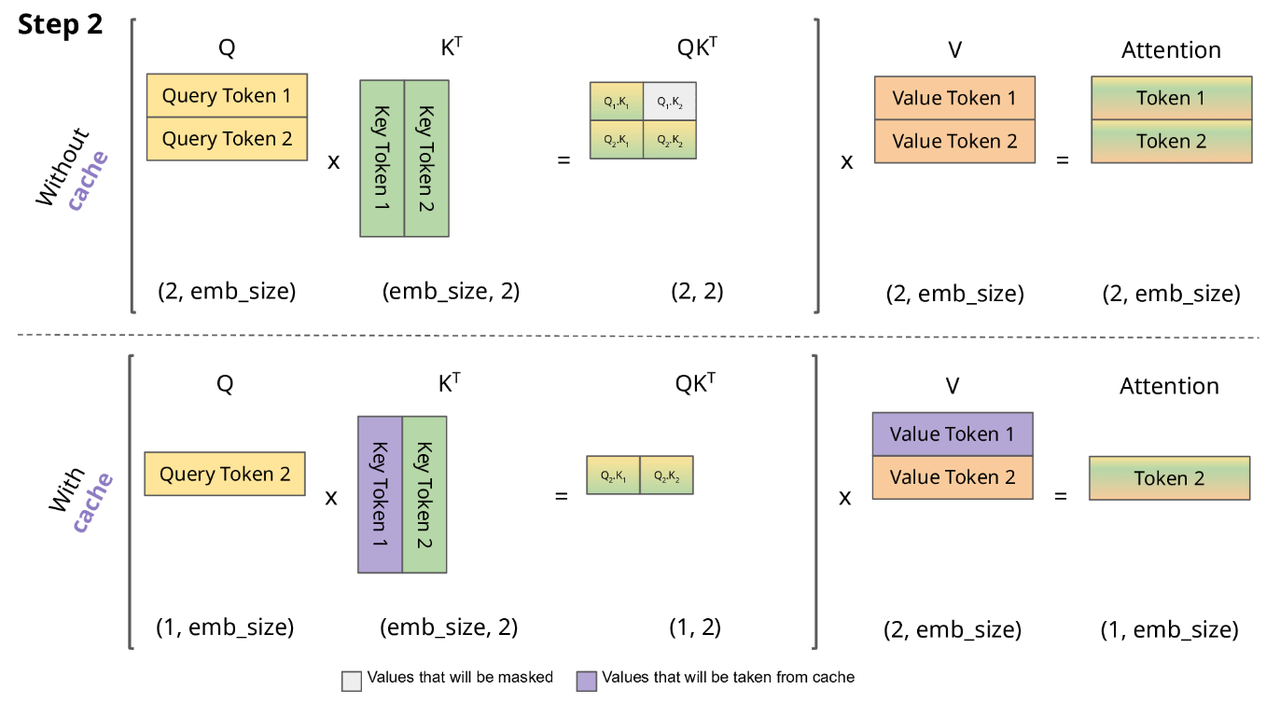
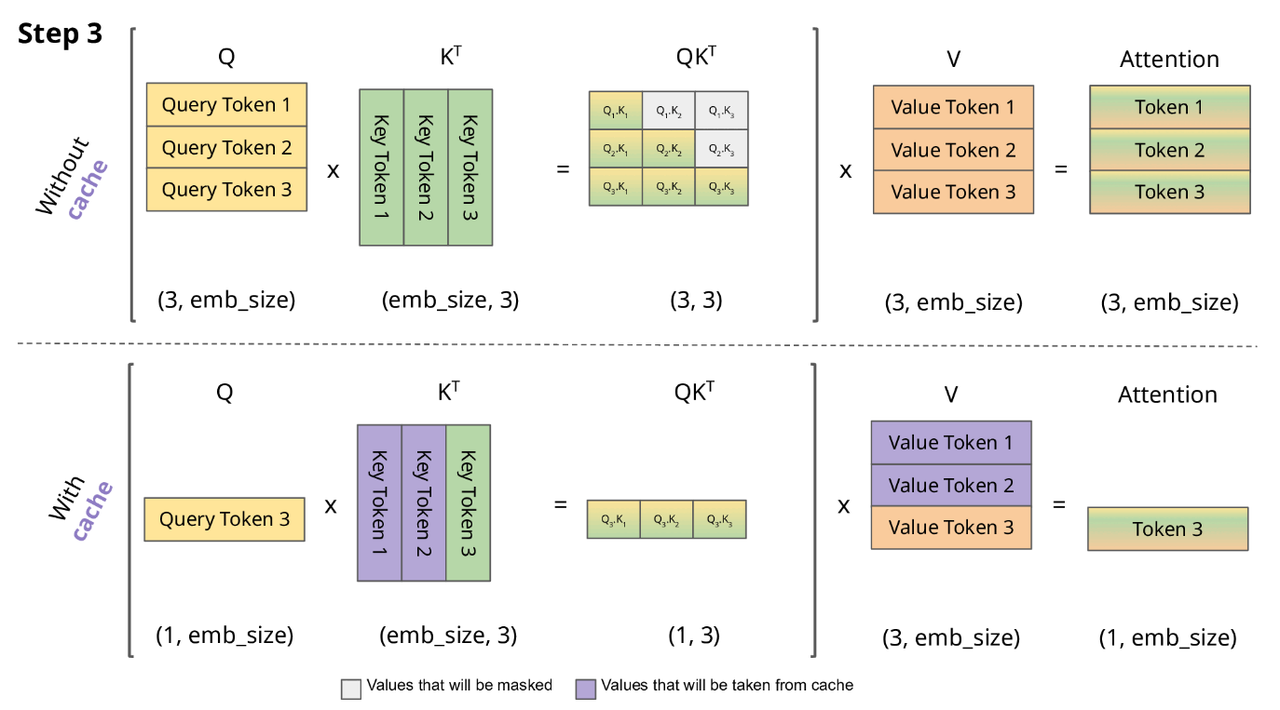
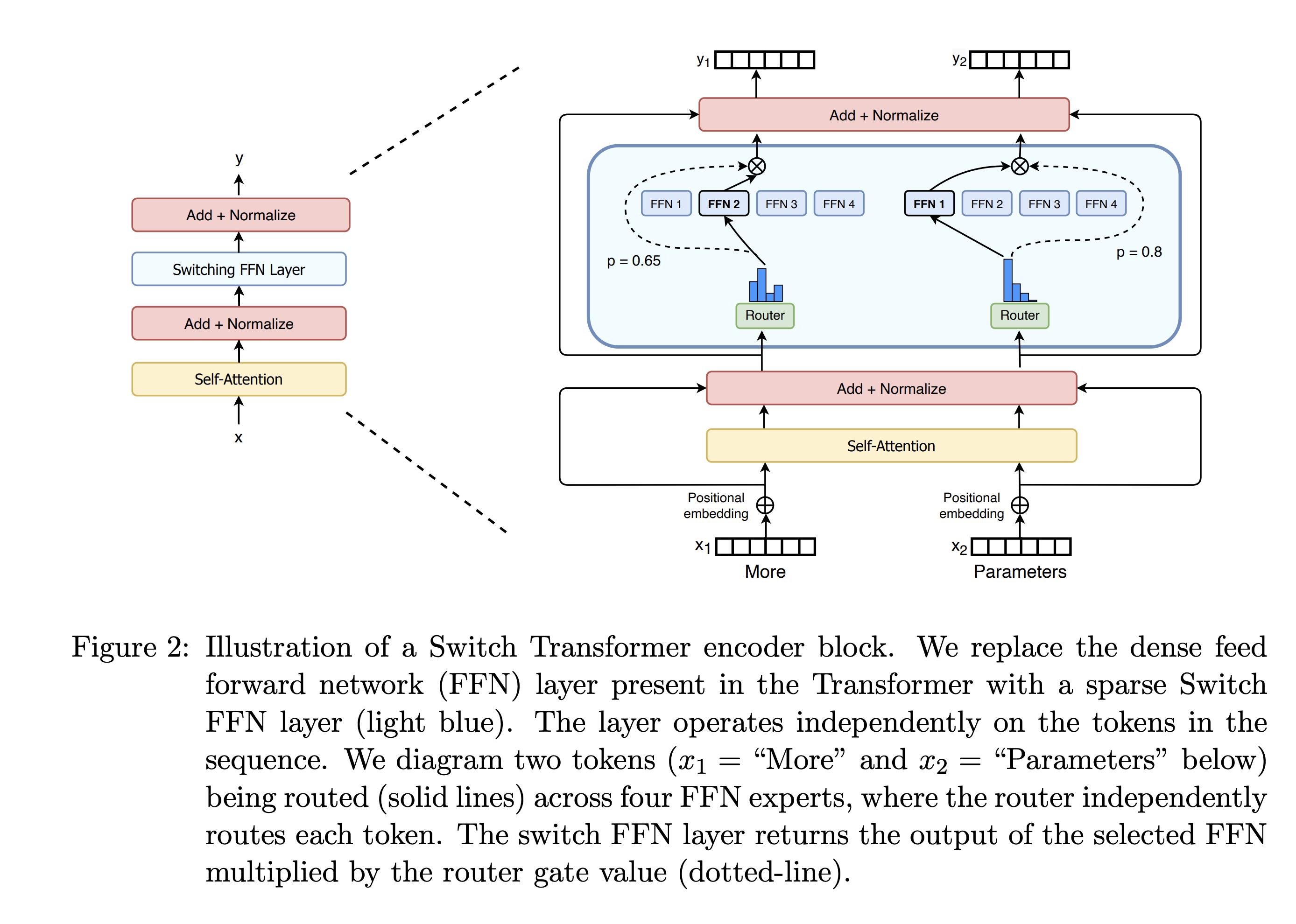 图片来自于Switch Transformers: Scaling to Trillion
Parameter Models with Simple and Efficient Sparsity 论文。
图片来自于Switch Transformers: Scaling to Trillion
Parameter Models with Simple and Efficient Sparsity 论文。