pack and unpack
pack
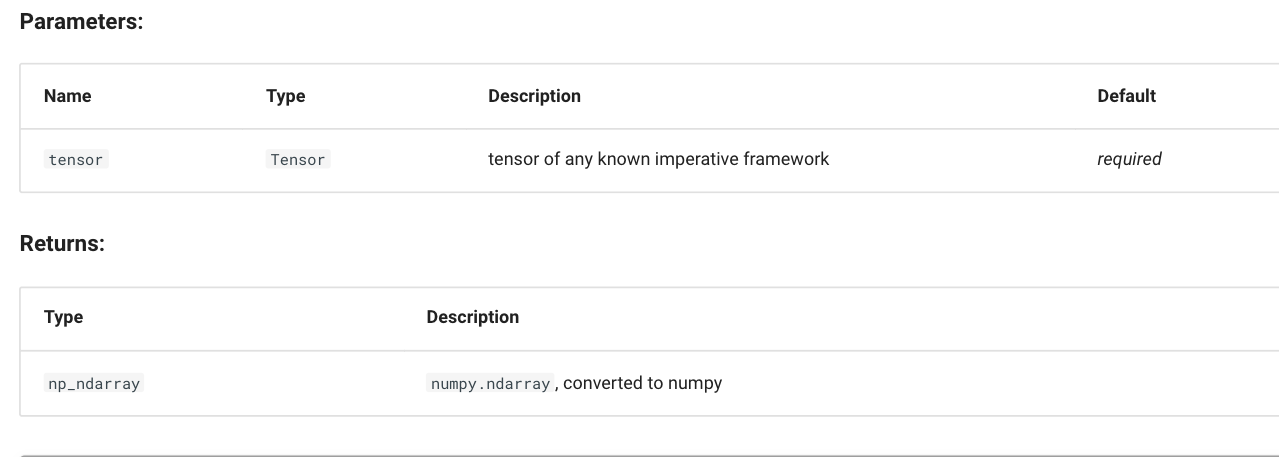
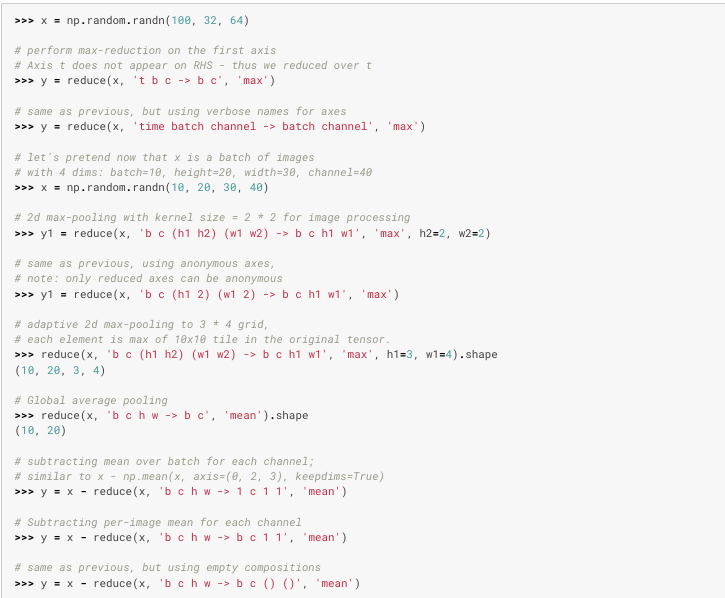
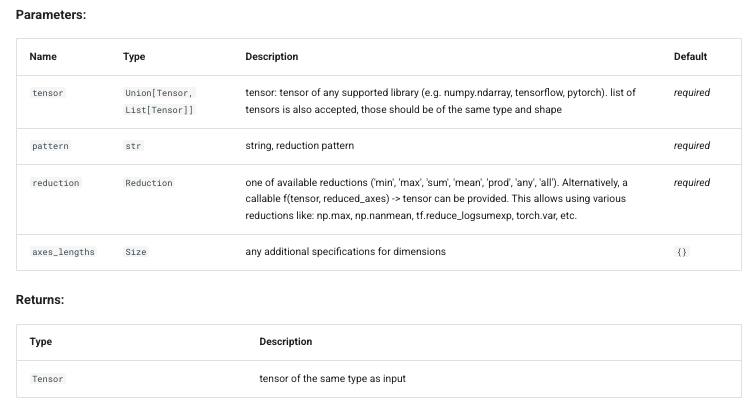
Packs several tensors into one. See einops tutorial for introduction into packing (and how it replaces stack and concatenation).
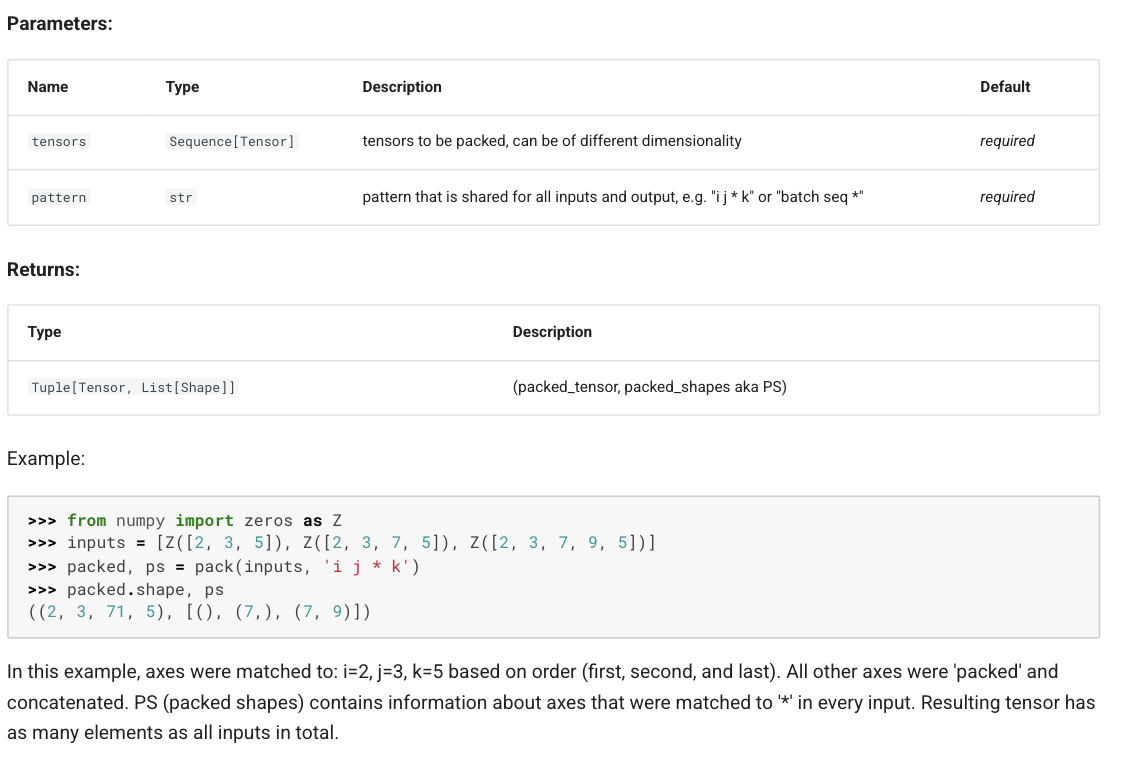 ## unpack >Unpacks a single tensor into several by
splitting over a selected axes. See einops tutorial for introduction
into packing (and how it replaces stack and concatenation).
## unpack >Unpacks a single tensor into several by
splitting over a selected axes. See einops tutorial for introduction
into packing (and how it replaces stack and concatenation).



 ## 应用
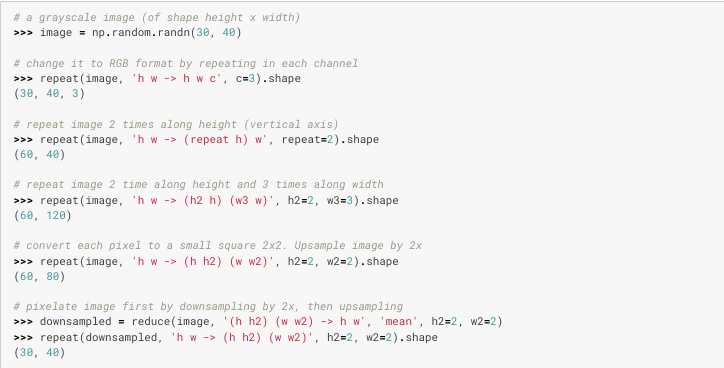
比如说repeat_kv函数就可以用einops.repeat很方便的实现
## 应用
比如说repeat_kv函数就可以用einops.repeat很方便的实现