init_workers详解
前置知识,ray前置知识 我将用此文来详细介绍veRL中有关single_controller和SPMD的相关内容。本文不涉及ppo训练相关,只是记录一下理解veRL架构实现的核心。
前置知识,ray前置知识 我将用此文来详细介绍veRL中有关single_controller和SPMD的相关内容。本文不涉及ppo训练相关,只是记录一下理解veRL架构实现的核心。
代码改编自# verl 解读 -
ray 相关前置知识 (part1)
ray分配资源的单位是bundle,一个bundle一般由1个cpu和1个gpu构成。
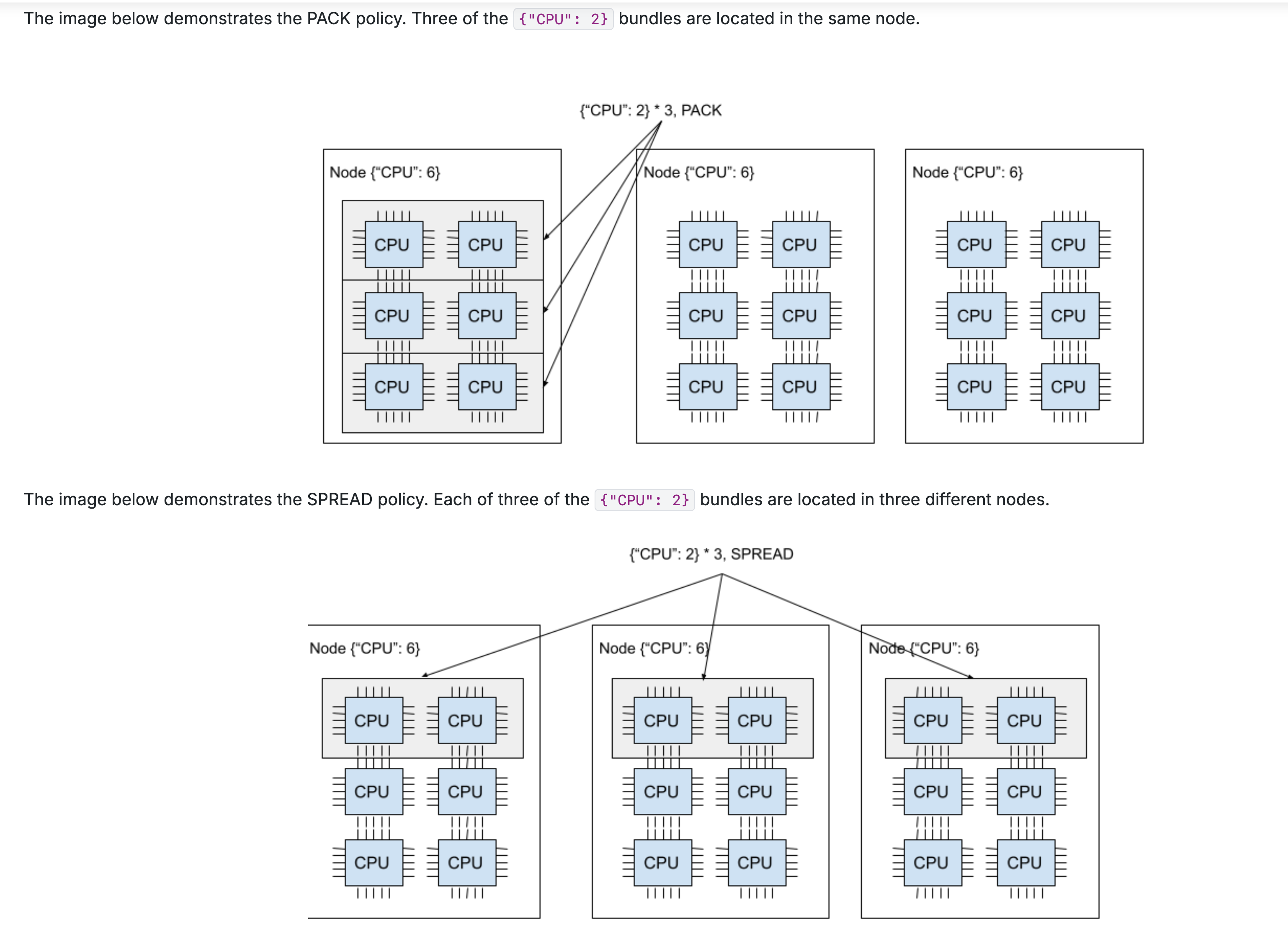
而一个placement_group由多个bundle组成,当参数设置为pack通常为同1个node上的bundle构成的。参数设置为spread为不同node的bundle组成。如下图所示:
根据Anthropic的定义,agent定义如下:
At Anthropic, we categorize all these variations as agentic systems, but draw an important architectural distinction between workflows and agents: Workflows are systems where LLMs and tools are orchestrated through predefined code paths. Agents, on the other hand, are systems where LLMs dynamically direct their own processes and tool usage, maintaining control over how they accomplish tasks.
在 RLHF 流程中,actor model 的 generation 和 rollout 占据了绝大多数运行时间(在 veRL 是 58.9%)。并且,由于 PPO 是 online 算法,经验(experiences)必须来自于被 train 的模型本身,因此,rollout 和 training 是必须串行的。如果这两者使用不同的资源组,比如 rollout 用 2 张卡,而 training 用 4 张卡,rollout 的时候 training 的资源闲置,training 的时候 rollout 的资源闲置,无论如何都会浪费大量的计算资源。由此,veRL 将 training 和 rollout engine 放置在同一个资源组中串行执行。training 时,将 rollout engine 的显存回收(offload 到 CPU 上 或者直接析构掉),rollout 时,再将 training engine 的显存释放掉。这种将 actor model 的不同 engine 放置在同一个资源组上的方案,就称为 hybrid engine。
最原生的reward_mananger:
class NaiveRewardManager:
"""The reward manager."""
def __init__(self, tokenizer, num_examine, compute_score=None, reward_fn_key="data_source") -> None:
self.tokenizer = tokenizer
self.num_examine = num_examine # the number of batches of decoded responses to print to the console
self.compute_score = compute_score or default_compute_score
self.reward_fn_key = reward_fn_key
def __call__(self, data: DataProto, return_dict=False):
"""We will expand this function gradually based on the available datasets"""
# If there is rm score, we directly return rm score. Otherwise, we compute via rm_score_fn
if "rm_scores" in data.batch.keys():
if return_dict:
return {"reward_tensor": data.batch["rm_scores"]}
else:
return data.batch["rm_scores"]
reward_tensor = torch.zeros_like(data.batch["responses"], dtype=torch.float32)
reward_extra_info = defaultdict(list)
already_print_data_sources = {}
for i in range(len(data)):
data_item = data[i] # DataProtoItem
prompt_ids = data_item.batch["prompts"]
prompt_length = prompt_ids.shape[-1]
valid_prompt_length = data_item.batch["attention_mask"][:prompt_length].sum()
valid_prompt_ids = prompt_ids[-valid_prompt_length:]
response_ids = data_item.batch["responses"]
valid_response_length = data_item.batch["attention_mask"][prompt_length:].sum()
valid_response_ids = response_ids[:valid_response_length]
# decode
prompt_str = self.tokenizer.decode(valid_prompt_ids, skip_special_tokens=True)
response_str = self.tokenizer.decode(valid_response_ids, skip_special_tokens=True)
ground_truth = data_item.non_tensor_batch["reward_model"]["ground_truth"]
data_source = data_item.non_tensor_batch[self.reward_fn_key]
extra_info = data_item.non_tensor_batch.get("extra_info", None)
score = self.compute_score(
data_source=data_source,
solution_str=response_str,
ground_truth=ground_truth,
extra_info=extra_info,
)
if isinstance(score, dict):
reward = score["score"]
# Store the information including original reward
for key, value in score.items():
reward_extra_info[key].append(value)
else:
reward = score
reward_tensor[i, valid_response_length - 1] = reward
if data_source not in already_print_data_sources:
already_print_data_sources[data_source] = 0
if already_print_data_sources[data_source] < self.num_examine:
already_print_data_sources[data_source] += 1
print("[prompt]", prompt_str)
print("[response]", response_str)
print("[ground_truth]", ground_truth)
if isinstance(score, dict):
for key, value in score.items():
print(f"[{key}]", value)
else:
print("[score]", score)
if return_dict:
return {
"reward_tensor": reward_tensor,
"reward_extra_info": reward_extra_info,
}
else:
return reward_tensor逻辑很简单,就是通过compute_score函数来计算score。
https://zhuanlan.zhihu.com/p/27278317894 rStar-Math: Small LLMs Can Master Math Reasoning with Self-Evolved Deep Thinking
a = 'global'
def outer():
# def len(in_var):
# print('called my len() function: ', end="")
# l = 0
# for i in in_var:
# l += 1
# return l
a = 'local'
def inner():
nonlocal a
a += ' variable'
inner()
print('a is', a)
# print(len(a))
outer()
# print(len(a))
print('a is', a)此时为nonlocal a,会按照local-闭包-global的顺序找到闭包变量a。a的值为local variable
python调试工具,类似于vscode的调试工具,使用命令行进行调试。
import pdb; pdb.set_trace()或者
breakpoint()python -m pdb [-c command] (-m module | pyfile) [args ...]即help,可用命令如下 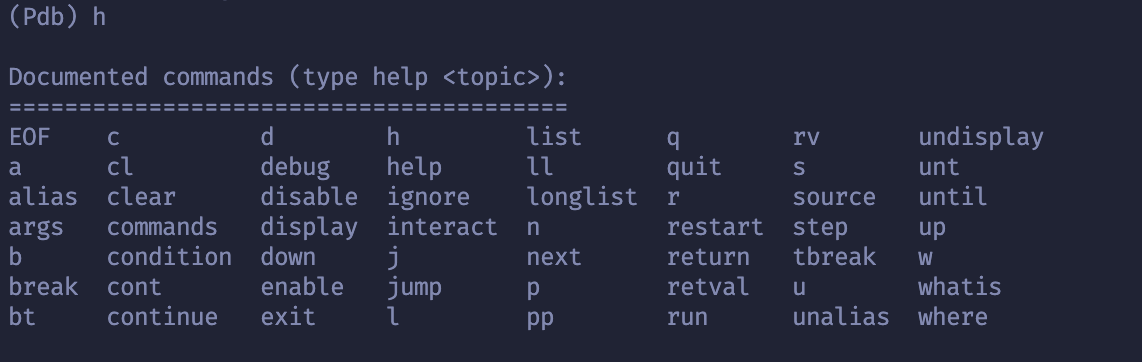
理论部分在这:generate相关 ## generate参数
def generate(
self,
inputs: Optional[torch.Tensor] = None,
generation_config: Optional[GenerationConfig] = None,
logits_processor: Optional[LogitsProcessorList] = None,
stopping_criteria: Optional[StoppingCriteriaList] = None,
prefix_allowed_tokens_fn: Optional[Callable[[int, torch.Tensor], List[int]]] = None,
synced_gpus: Optional[bool] = None,
assistant_model: Optional["PreTrainedModel"] = None,
streamer: Optional["BaseStreamer"] = None,
negative_prompt_ids: Optional[torch.Tensor] = None,
negative_prompt_attention_mask: Optional[torch.Tensor] = None,
**kwargs,
) -> Union[GenerateOutput, torch.LongTensor]:在代码中可以看到在函数入口显式的定义了很多参数。他们的具体含义如下
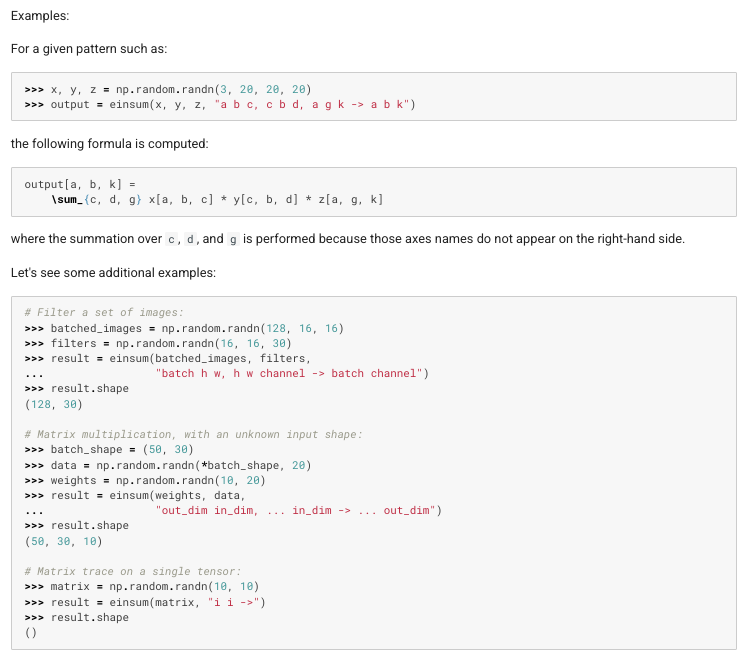
einops.einsum calls einsum operations with einops-style named axes indexing, computing tensor products with an arbitrary number of tensors. Unlike typical einsum syntax, here you must pass tensors first, and then the pattern.
Also, note that rearrange operations such as
"(batch chan) out", or singleton axes(), are not currently supported.
爱因斯坦求和