AdamW相对与Adam的改动十分简单，其将权重衰减项从梯度的计算中拿出来直接加在了最后的权重更新步骤上（图1，式12）。其提出的动机在于：原先Adam的实现中如果采用了 L2权重衰减，则相应的权重衰减项会被直接加在loss里，从而导致动量的一阶与二阶滑动平均均考虑了该权重衰减项，而这影响了Adam的优化效果，而将权重衰减与梯度的计算进行解耦能够显著提升Adam的效果。目前，AdamW现在已经成为transformer训练中的默认优化器了。

RMSProp 和 Adagrad 算法的最大区别就是在于更新累积梯度值 r 的时候 RMSProp 考虑加入了一个权重系数 ρ 。 它使用了一个梯度平方的滑动平均。其主要思路就是考虑历史的梯度，对于离得近的梯度重点考虑，而距离比较远的梯度则逐渐忽略。注意图中的是内积。

作为机器学习的初学者必然会接触梯度下降算法以及 SGD，基本上形式如下：

\[ \theta_t = \theta_{t-1} - \alpha \;g(\theta) \] 其中 \(\alpha\) 为学习率，\(g(\theta)\) 为梯度。

带动量的随机梯度下降方法

它的思路就是计算前面梯度的该变量，每次迭代会考虑前面的计算结果。这样如果在某个维度上波动厉害的特征，会由于“momentum”的影响，而抵消波动的方向（因为波动剧烈的维度每次更新的方向是相反的，momentum 能抵消这种波动）。使得梯度下降更加的平滑，得到更快的收敛效率。而后续提出的 Adagrad，RMSProp 以及结合两者优点的 Adam 算法都考虑了这种“momentum”的思想。

前置阅读：MHA 、MQA、GQA 和 rope

在标准的 Transformer中，多头注意力（Multi-Head Attention, MHA）机制通过并行计算多个注意力头来捕捉输入序列中的不同特征。每个注意力头都有自己的查询（Query, Q）、键（Key, K）和值（Value, V）矩阵，计算过程如下：

Muon 算法流程如下图所示：

其中最主要的部分是 NewtonSchulz 5 算法，流程如下：

def newtonschulz5(G, steps=5, eps=1e-7):
    assert G.ndim == 2
    
    a, b, c = (3.4445, -4.7750, 2.0315)
    
    X = G.bfloat16()
    
    X /= (X.norm() + eps)
    
    if G.size(0) > G.size(1):
    
    X = X.T
    
    for _ in range(steps):
    
    A = X @ X.T
    
    B = b * A + c * A @ A
    
    X = a * X + B @ X
    
    if G.size(0) > G.size(1):
    
    X = X.T
    
    return X

这个算法的作用是将 G 近似为一个最接近他的半正交矩阵，即：

为什么存储激活值？

首先回顾为什么要存储激活值。 简单来说，模型参数是根据导数更新的。为了有效地计算这些导数，必须缓存某些张量。激活内存是这些缓存张量的内存成本。 具体来说，以 \(f\) 是矩阵乘法运算：

CPU 卸载允许我们将一些状态传输到 CPU，因此我们不必将所有内容都保存在 GPU RAM 中。虽然 CPU作比 GPU作慢，但将不常访问的数据移动到 CPU 内存可以帮助我们保持在 GPU 内存限制范围内。

梯度累积使我们能够通过按顺序处理较小的批次来扩展到更大的有效批次。我们不是一次计算整个批次的梯度（这需要将所有激活存储在内存中），而是在更新模型参数之前将每个小批次的梯度相加。这减少了内存使用量，但需要更多的向前/向后传递。

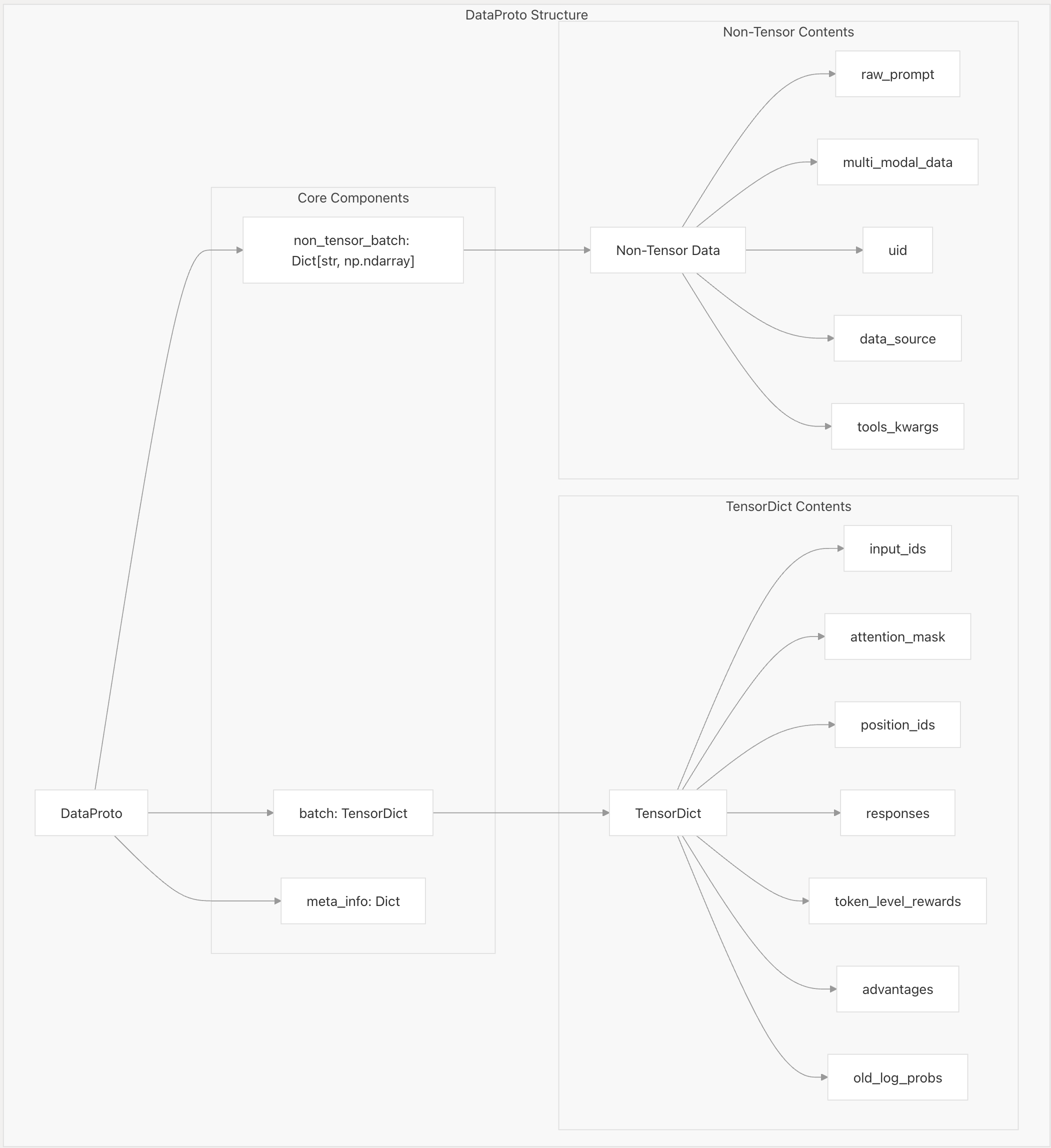
从上图中可以看到DataProto可以分为3个部分： - non_tensor_batch - batch - meta_info 其中non_tensor_batch和meta_info都是个字典，而batch是TensorDict类型的变量。