参考：https://cuijiahua.com/blog/2017/12/ml_13_regtree_1.html

1、ID3算法的弊端

回忆一下，决策树的树构建算法是ID3。ID3的做法是每次选取当前最佳的特征来分割数据，并按照该特征的所有可能取值来切分。也就是说，如果一个特征有4种取值，那么数据将被切分成4份。一旦按某特征切分后，该特征在之后的算法执行过程中将不会再起作用，所以有观点认为这种切分方式过于迅速。

搜索旋转排序数组

题目：

https://leetcode-cn.com/problems/search-in-rotated-sorted-array/

思路：

明显的二分查找，不过不是有序数组了，而是部分有序，所以需要有判断

代码：

class Solution(object):
    def search(self, nums, target):
        left, right = 0, len(nums) - 1
        while left <= right:
            mid = left + (right - left) // 2
            if nums[mid] == target:
                return mid
            if nums[mid] < nums[right]:#右边为升序
                if nums[mid] < target <= nums[right]:
                    left = mid + 1
                else:
                    right = mid 
            if nums[left] <= nums[mid]:#左边为升序
                if nums[left] <= target < nums[mid]:
                    right = mid 
                else:
                    left = mid + 1
        return -1

pandas补充学习

推荐网站：http://joyfulpandas.datawhale.club/Content/Preface.html

pandas核心操作手册：https://mp.weixin.qq.com/s/l1V5e726XixI0W3EDHx0Nw

pd.join和pd.merge

可以说merge包含了join操作，merge支持两个df间行方向或列方向的拼接操作，默认列拼接，取交集，而join只是简化了merge的行拼接的操作 pandas的merge方法提供了一种类似于SQL的内存链接操作，官网文档提到它的性能会比其他开源语言的数据操作（例如R）要高效。 如果对于sql比较熟悉的话，merge也比较好理解。 merge的参数

线性判别分析(LDA)

线性判别分析，也就是LDA（与主题模型中的LDA区分开），现在常常用于数据的降维中，但从它的名字中可以看出来它也是一个分类的算法，而且属于硬分类，也就是结果不是概率，是具体的类别 ## 主要思想 1. 类内方差小 2. 类间方差大 ## 推导 这里以二类为例，即只有两个类别。

条件概率

\(P(B|A) = \frac{P(AB)}{P(A)}\)

乘法法则

如果P(A) > 0 \(P(AB) = P(A)P(B|A)\) 如果\(P(A_1 \dots A_{n-1})\) > 0 则

\[ \begin{aligned} P(A_1A_2\dots A_n) = P(A_1A_2\dots A_{n-1})P(A_n | A_1A_2\dots A_{n-1}) \\\\ = P(A_1)P(A_2|A_1)P(A_3|A_1A_2)\dots P(A_n|A_1A_2\dots A_{n-1}) \end{aligned} \]

其中第一步使用了乘法公式，然后再对前者继续使用乘法公式，以此类推，就可以得到最后的结果。

正为逆时针转，负为顺时针转。

import numpy as np
mat = np.array([[1,3,5],
                [2,4,6],
                [7,8,9]
                ])
print mat, "# orignal"
mat90 = np.rot90(mat, 1)
print mat90, "# rorate 90 <left> anti-clockwise"
mat90 = np.rot90(mat, -1)
print mat90, "# rorate 90 <right> clockwise"
mat180 = np.rot90(mat, 2)
print mat180, "# rorate 180 <left> anti-clockwise"
mat270 = np.rot90(mat, 3)
print mat270, "# rorate 270 <left> anti-clockwise"

直接复制的代码，python2，能看懂就行。

数据挖掘比赛

对赛题进行理解

数据分析

EDA目标

• EDA的价值在于熟悉数据集，了解数据集，对数据集进行验证来确定所获得数据集可以用于接下来的机器学习或者深度学习使用。
• 当了解了数据集之后我们下一步就是要去了解变量间的相互关系以及变量与预测值之间的存在关系。
• 引导数据科学从业者进行数据处理以及特征工程的步骤,使数据集的结构和特征集让接下来的预测问题更加可靠。
• 完成对于数据的探索性分析，并对于数据进行一些图表或者文字总结并打卡。

主要操作

1. 载入各种数据科学以及可视化库:
   • 数据科学库 pandas、numpy、scipy；
   • 可视化库 matplotlib、seabon；
   • 其他；
2. 载入数据：
   • 载入训练集和测试集；
   • 简略观察数据(head()+shape)；
3. 数据总览:
   • 通过describe()来熟悉数据的相关统计量
   • 通过info()来熟悉数据类型
4. 判断数据缺失和异常
   • 查看每列的存在nan情况
   • 异常值检测
5. 了解预测值的分布
   • 总体分布概况（无界约翰逊分布等）
   • 查看skewness and kurtosis
   • 查看预测值的具体频数
6. 特征分为类别特征和数字特征，并对类别特征查看unique分布
7. 数字特征分析
   • 相关性分析
   • 查看几个特征得 偏度和峰值
   • 每个数字特征得分布可视化
   • 数字特征相互之间的关系可视化
   • 多变量互相回归关系可视化
8. 类型特征分析
   • unique分布
   • 类别特征箱形图可视化
   • 类别特征的小提琴图可视化
   • 类别特征的柱形图可视化类别
   • 特征的每个类别频数可视化(count_plot)
9. 用pandas_profiling生成数据报告

主要步骤

1. 对于数据的初步分析（直接查看数据，或.sum(), .mean()，.descirbe()等统计函数）可以从：样本数量，训练集数量，是否有时间特征，是否是时许问题，特征所表示的含义（非匿名特征），特征类型（字符类似，int，float，time），特征的缺失情况（注意缺失的在数据中的表现形式，有些是空的有些是”NAN”符号等），特征的均值方差情况。
2. 分析记录某些特征值缺失占比30%以上样本的缺失处理，有助于后续的模型验证和调节，分析特征应该是填充（填充方式是什么，均值填充，0填充，众数填充等），还是舍去，还是先做样本分类用不同的特征模型去预测。
3. 对于异常值做专门的分析，分析特征异常的label是否为异常值（或者偏离均值较远或者事特殊符号）,异常值是否应该剔除，还是用正常值填充，是记录异常，还是机器本身异常等。
4. 对于Label做专门的分析，分析标签的分布情况等。
5. 进步分析可以通过对特征作图，特征和label联合做图（统计图，离散图），直观了解特征的分布情况，通过这一步也可以发现数据之中的一些异常值等，通过箱型图分析一些特征值的偏离情况，对于特征和特征联合作图，对于特征和label联合作图，分析其中的一些关联性。

记录自己之前没用到的东西 ### 数据的偏度和峰度 - 数据的偏度(skewness)：dataframe.skew() - 数据的峰度(kurtosis)：dataframe.kurt() ### log变换 一般要求预测值需要符合正态分布，因此需要先log变换一下 ### sns.pairplot 用来展现变量两两之间的关系，比如线性、非线性、相关 hue参数可以指定分类。

什么是前缀树？

前缀树是N叉树的一种特殊形式。通常来说，一个前缀树是用来存储字符串的。前缀树的每一个节点代表一个字符串（前缀）。每一个节点会有多个子节点，通往不同子节点的路径上有着不同的字符。子节点代表的字符串是由节点本身的原始字符串，以及通往该子节点路径上所有的字符组成的。 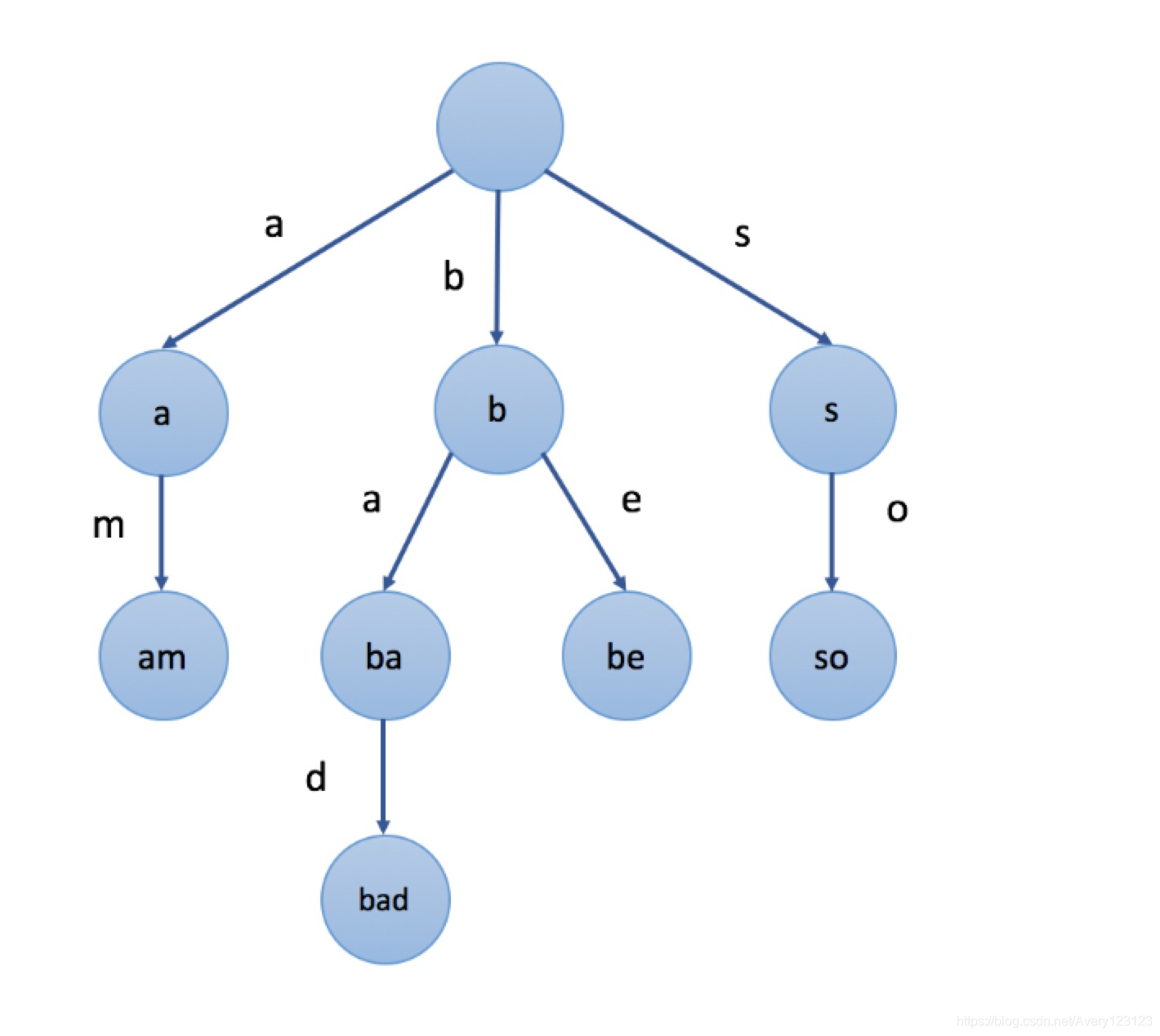在上图示例中，我们在节点中标记的值是该节点对应表示的字符串。例如，我们从根节点开始，选择第二条路径 ‘b’，然后选择它的第一个子节点 ‘a’，接下来继续选择子节点 ‘d’，我们最终会到达叶节点 “bad”。节点的值是由从根节点开始，与其经过的路径中的字符按顺序形成的。

Logistic回归

线性回归

线性回归表达式：

\[ y = w^Tx+b \]

广义回归模型：

\[ y = g^{-1}(w^Tx+b) \]

Sigmoid函数

在分类任务中，需要找到一个联系函数，即g，将线性回归的输出值与实际的标签值联系起来。因此可以使用Sigmoid函数 即：