分类算法概述

vllbc 发布于 2022-08-12 收录于 Machine Learning 分类算法

分类算法

主要区分一下生成模型和判别模型，首先要知道生成模型和判别模型都属于监督学习，即样本有其对应的标签的。还有一个概念就是硬分类和软分类，简单理解就是硬分类是直接分出类别，比如线性判别分析、感知机。而软分类是计算出概率，根据概率来得到类别，生成模型和判别模型都是软分类。

BM25

vllbc 发布于 2022-08-07 收录于 NLP

BM25算法

BM25算法，通常用来作搜索相关性平分。一句话概况其主要思想：对Query进行语素解析，生成语素qi；然后，对于每个搜索结果D，计算每个语素qi与D的相关性得分，最后，将qi相对于D的相关性得分进行加权求和，从而得到Query与D的相关性得分。

GPT

vllbc 发布于 2022-07-27 收录于 NLP

GPT

预训练(从左到右的 Transformer 语言模型)

GPT 是一种基于 Transformer 的从左到右的语言模型。该架构是一个 12 层的 Transformer 解码器（没有解码器-编码器）。 ## 模型架构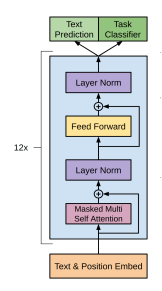

就是12层的transformer-decoder。其中只使用了transformer模型中的decoder部分，并且把decoder里面的encoder-decoder attention部分去掉了，只保留了masked self-attention，再加上feed-forward部分。再提一句，masked self-attention保证了GPT模型是一个单向的语言模型。另外，作者在position encoding上做了调整，使用了可学习的位置编码，不同于transformer的三角函数位置编码。

Dropout正则化

vllbc 发布于 2022-07-21 收录于 Deep Learning 网络正则化

Dropout

在标准dropout正则化中，通过按保留（未丢弃）的节点的分数进行归一化来消除每一层的偏差。换言之，每个中间激活值h以保留概率概率p由随机变量替换(即drop经过神经元后的值代替drop神经元)

最长回文子串

vllbc 发布于 2022-07-21 收录于算法题

最长回文子串

题目：

https://leetcode-cn.com/problems/longest-palindromic-substring/

思路：

一开始暴力解法，比较好想，结果超时了哎，后来看见了标签是动态规划，才知道不能暴力

class Solution:
    def longestPalindrome(self, s: str) -> str:
        if len(s) <= 1:
            return s
        maxs = -float("inf")
        res = collections.defaultdict(list)
        left,right = 0,len(s)-1
        while left < right:
            for i in range(left,right+2):
                if s[left:i] == s[left:i][::-1]:
                    maxs = max(maxs,len(s[left:i]))
                    res[maxs].append(s[left:i])
            left += 1
        return max(res[max(res.keys())],key=len)

也用到了双指针，超时在情理之中。

有效的数独

vllbc 发布于 2022-07-20 收录于算法题

有效的数独

https://leetcode-cn.com/problems/valid-sudoku/

#有效的数独 难点在将3*3里的数取出来


class Solution:
    def isValidSudoku(board) -> bool:
        for line1,line2 in zip(board,zip(*board)): #行列
            for n1,n2 in zip(line1,line2):
                if (n1 != '.' and line1.count(n1) > 1) or (n2!='.' and line2.count(n2) >1):
                    return False
        pal = [[board[i+m][j+n] for m in range(3) for n in range(3) if board[i+m][j+n] != '.'] for i in (0, 3, 6) for j in (0, 3, 6)]
        for line in pal:
            if len(set(line)) != len(line):
                return False
        return True

Apriori算法

vllbc 发布于 2022-07-18 收录于 Machine Learning 关联规则算法

使括号有效的最少添加

vllbc 发布于 2022-07-17 收录于算法题

使括号有效的最少添加

题目：

https://leetcode-cn.com/problems/minimum-add-to-make-parentheses-valid/

思路：

通过一个值来判断是否匹配

代码：

class Solution:
    def minAddToMakeValid(self, S: str) -> int:
        res,temp = 0,0
        for i in S:
            if i == '(':
                temp += 1
            if i == ')':
                temp -= 1
                if temp == -1:
                    temp = 0
                    res += 1
        return res + temp

如果右括号过多的话，就在左边补一个左括号。这时结果+1

Ensemble Learning

vllbc 发布于 2022-07-09 收录于 Machine Learning 集成学习

集成学习

在机器学习的有监督学习算法中，我们的目标是学习出一个稳定的且在各个方面表现都较好的模型，但实际情况往往不这么理想，有时我们只能得到多个有偏好的模型（弱监督模型，在某些方面表现的比较好）。集成学习就是组合这里的多个弱监督模型以期得到一个更好更全面的强监督模型，集成学习潜在的思想是即便某一个弱分类器得到了错误的预测，其他的弱分类器也可以将错误纠正回来。集成学习在各个规模的数据集上都有很好的策略。数据集大：划分成多个小数据集，学习多个模型进行组合数据集小：利用Bootstrap方法进行抽样，得到多个数据集，分别训练多个模型再进行组合

旋转图像

vllbc 发布于 2022-07-07 收录于算法题

旋转图像

https://leetcode-cn.com/problems/rotate-image/

没难度的中等题，这方法很python

class Solution:
    def rotate(self, matrix: List[List[int]]) -> None:
        """
        Do not return anything, modify matrix in-place instead.
        """
        n = len(matrix)
        for i in list(map(list,map(reversed,zip(*matrix)))):
            matrix.append(i)
        del matrix[:n]