Muon
Muon 算法流程如下图所示:

其中最主要的部分是 NewtonSchulz 5 算法,流程如下:
def newtonschulz5(G, steps=5, eps=1e-7):
assert G.ndim == 2
a, b, c = (3.4445, -4.7750, 2.0315)
X = G.bfloat16()
X /= (X.norm() + eps)
if G.size(0) > G.size(1):
X = X.T
for _ in range(steps):
A = X @ X.T
B = b * A + c * A @ A
X = a * X + B @ X
if G.size(0) > G.size(1):
X = X.T
return X这个算法的作用是将 G 近似为一个最接近他的半正交矩阵,即:
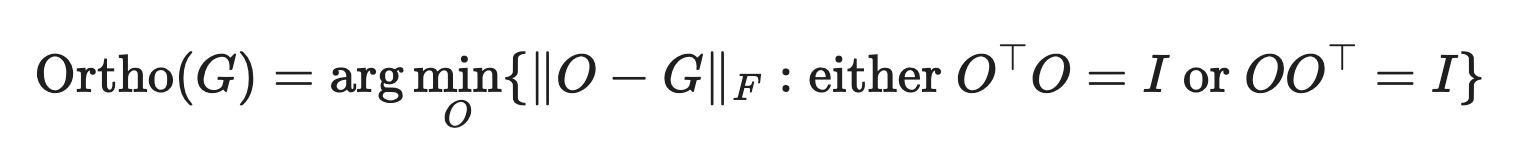
对于经验动机,我们观察到,基于手动检查,SGD-momentum 和 Adam 对基于 Transformer 的神经网络中的 2D 参数产生的更新通常具有非常高的条件数。也就是说,它们几乎是低秩矩阵,所有神经元的更新仅由几个方向主导。我们推测正交化有效地增加了其他“罕见方向”的规模,这些方向在更新中幅度较小,但对学习仍然很重要。
Muon in Moonlight
来自Muon续集:为什么我们选择尝试Muon? - 科学空间|Scientific Spaces ### Weight Decay
kimi团队研究发现如果不加上权重衰减收敛速度到后面会被adam追上,因此加上了权重衰减:
\[ \Delta W =-\eta[msign(M) + \lambda W] \]
总的来说,这种做法可以缓解MaxLogit爆炸的问题,因为qk相乘的结果和xq、xk以及Wq和Wk有关,x会经过rmsnorm,所以爆炸的原因来自于W的爆炸,所以权重衰减可以缓解这个问题。
RMS对齐
我理解为这是一种将Adam调好的超参数用到其它优化器的方法。
QK-clip
QK-norm可以很好的压制MaxLogit,但它只适用于MHA、GQA,不适用于MLA的推理阶段。因为推理阶段的Wk被吸收到了Q中。
这时候就需要返璞归真,既然MaxLogit太大,那就设定一个阈值,当Logit的值超过阈值的时候,就 直接裁剪到这个阈值。
这就有了他们最初始的想法(因为Logit是\(QK^T\),目的是在\(QK^T\)上进行裁剪,所以要对各自的参数矩阵裁剪sqrt。):
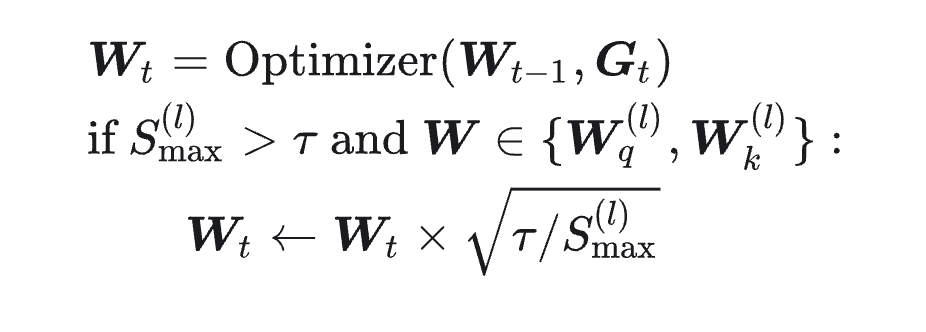
如果max_logit(在batch上也要找最大)大于阈值并且即将优化的参数是q或者k的线性矩阵参数,就将矩阵参数进行clip,来达到缩放max_logit的目的。
但后面他们发现这样一刀切很容易伤及无辜,因为多头注意力中,有可能只有1个头出现了max_logit超出阈值,但其它头的参数也会被裁减。
我们知道,不管哪种Attention变体都有多个Head,一开始我们是每一层Attention只监控一个MaxLogit指标,所有Head的Logit是放在一起取Max的,这导致QK-Clip也是所有Head一起Clip的。然而,当我们分别监控每个Head的MaxLogit后发现,实际上每层只有为数不多的Head会出现MaxLogit爆炸,如果所有Head按同一个比例来Clip,那么大部份Head都是被“无辜受累”的了,这就是过度裁剪的含义。
简单来说,QK-Clip的操作是乘以一个小于1的数,这个数对于MaxLogit爆炸的Head来说是刚刚好抵消增长趋势,但是对于其他head来说是单纯的缩小(它们没有增长趋势或者增长趋势很弱)。由于长期无端被乘一个小于1的数,那么很容易出现就趋于零的现象,这是“过度裁剪”的表现。
因此还需要监控各个头的max_logit,如果某个头出现了这个问题,那么就单独对这个头的参数矩阵进行裁剪。但这里有一个问题就是,对于MLA而言,并不是简单的存在Wq和Wk,而是Wqc、Wkc、Wqr、Wkr,而Wkr是所有的head共享的,如果裁剪Wkr也会导致出现无辜头,所以只需要裁剪Wqr。
所以最终版本如下:
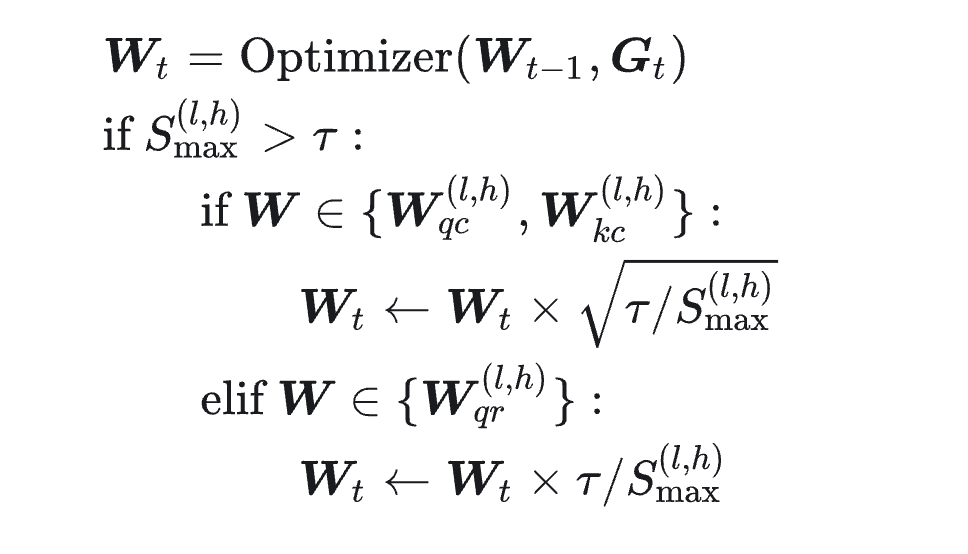
将QK-clip应用到Muon优化器就变成了Muon-Clip:


对比原生Muon可见改进了蛮多。 