MHA

Self-attention

首先介绍一下最主要的 self-attention，可以说是 self-attention 实现了上述的 token 之间交互的功能。

自注意力是模型的关键组成部分之一。注意和自注意之间的区别在于，自注意在相同性质的表示之间运行：例如，某个层中的所有编码器状态。

形式上，这种直觉是通过查询键值注意来实现的。Self-attention 中的每个输入标记都会收到三种表示，对应于它可以扮演的角色：

• Query
• Key
• Value

进入正题：

作为我们想要翻译的输入语句“The animal didn’t cross the street because it was too tired”。句子中”it”指的是什么呢？“it”指的是”street” 还是“animal”？对人来说很简单的问题，但是对算法而言并不简单。
当模型处理单词“it”时，self-attention 允许将“it”和“animal”联系起来。当模型处理每个位置的词时，self-attention 允许模型看到句子的其他位置信息作辅助线索来更好地编码当前词。如果你对 RNN 熟悉，就能想到 RNN 的隐状态是如何允许之前的词向量来解释合成当前词的解释向量。Transformer 使用 self-attention 来将相关词的理解编码到当前词中。

下面看一下 self-attention 是如何计算的：

向量计算

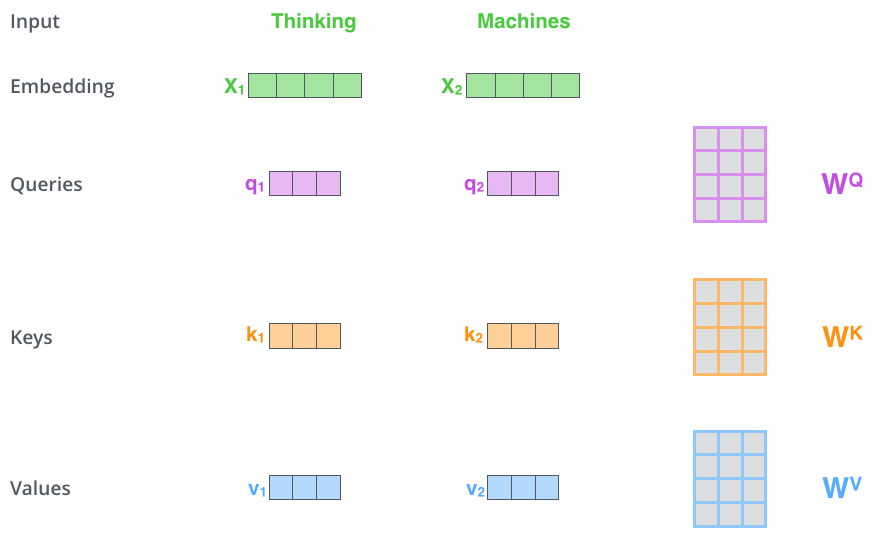
第一步，根据编码器的输入向量，生成三个向量，比如，对每个词向量，生成 query-vec, key-vec, value-vec，生成方法为分别乘以三个矩阵，这些矩阵在训练过程中需要学习。【注意：不是每个词向量独享 3 个 matrix，而是所有输入共享 3 个转换矩阵；权重矩阵是基于输入位置的转换矩阵；有个可以尝试的点，如果每个词独享一个转换矩阵，会不会效果更厉害呢？】
注意到这些新向量的维度比输入词向量的维度要小（512–>64），并不是必须要小的，是为了让多头 attention 的计算更稳定。

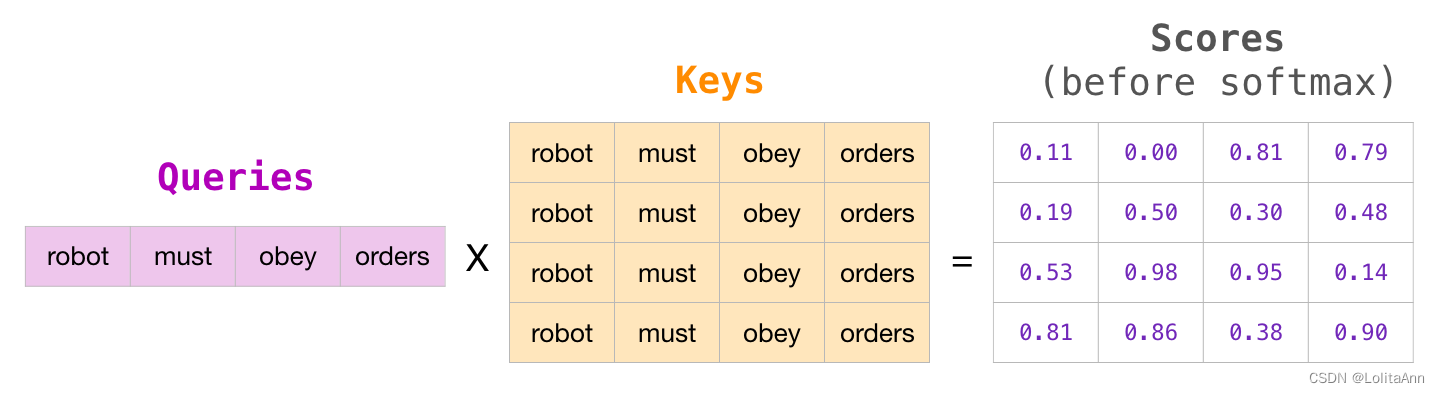
第二步，计算 attention 就是计算一个分值。对“Thinking Matchines”这句话，对“Thinking”（pos #1 ）计算 attention 分值。我们需要计算每个词与“Thinking”的评估分，这个分决定着编码“Thinking”时（某个固定位置时），每个输入词需要集中多少关注度。
这个分，通过“Thing”对应 query-vector 与所有词的 key-vec 依次做点积得到。所以当我们处理位置 #1时 ，第一个分值是 q 1 和 k 1 的点积，第二个分值是 q 1 和 k 2 的点积。这也就是所谓的注意力得分.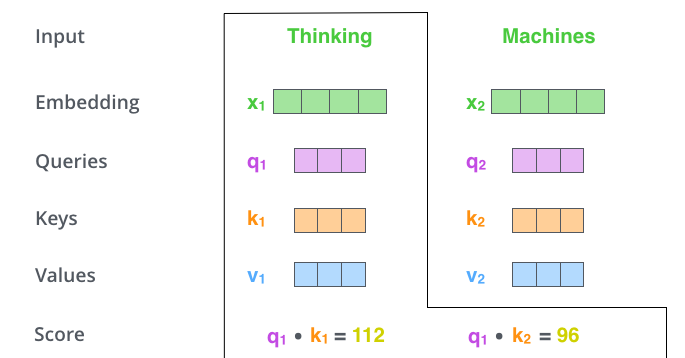

第三步和第四步，除以 8 (\(=\sqrt{dim_{key}}\))，这样梯度会更稳定。然后加上 softmax 操作，归一化分值使得全为正数且加和为 1。

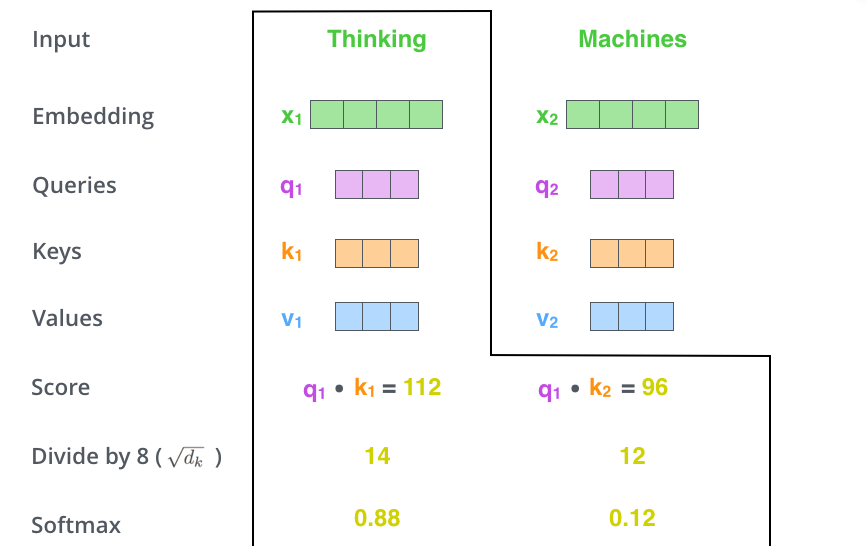
Softmax 分值决定着在这个位置，每个词的表达程度（关注度）。很明显，这个位置的词应该有最高的归一化分数，但大部分时候总是有助于关注该词的相关的词。

第五步，将 softmax 分值与 value-vec 按位相乘。保留关注词的 value 值，削弱非相关词的 value 值。

第六步，将所有加权向量加和，产生该位置的 self-attention 的输出结果。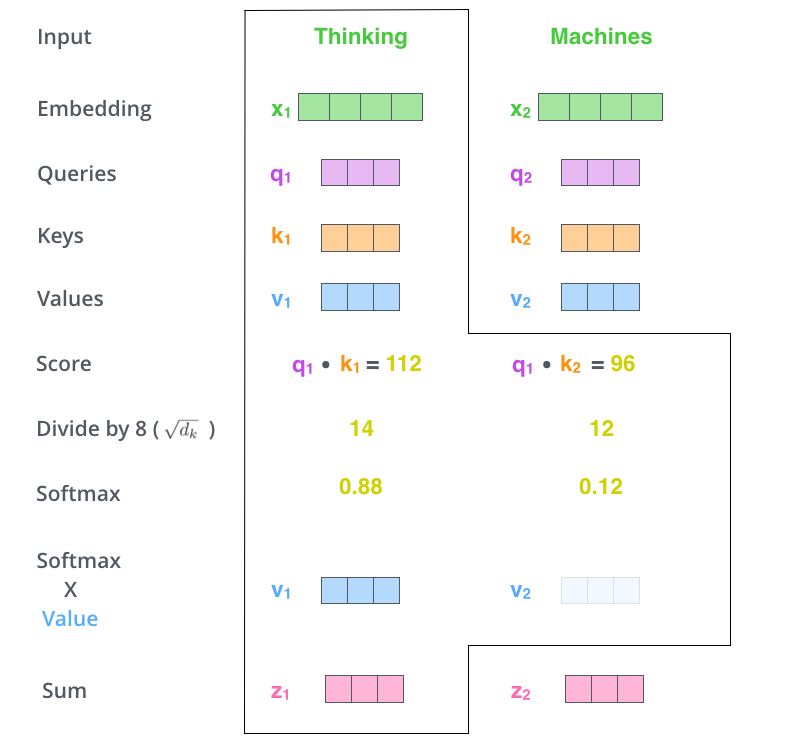

上述就是 self-attention 的计算过程，生成的向量流入前向网络。在实际应用中，上述计算是以速度更快的矩阵形式进行的。下面我们看下在单词级别的矩阵计算。

矩阵计算

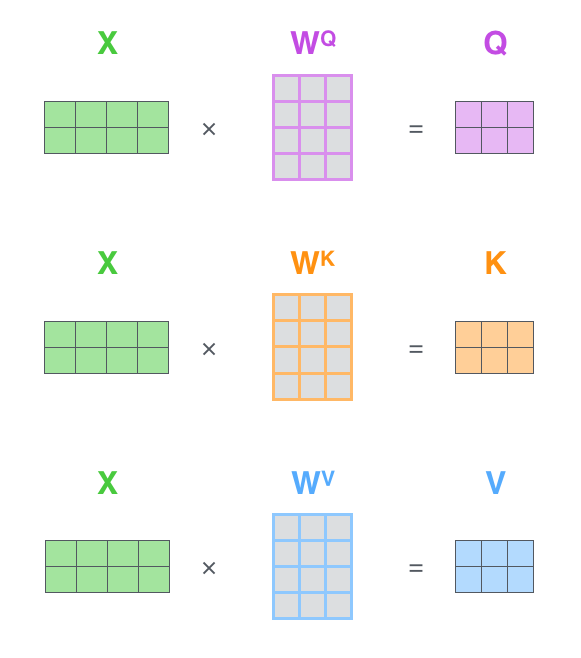
第一步，计算 query/key/value matrix，将所有输入词向量合并成输入矩阵 \(X\)，并且将其分别乘以权重矩阵 \(W^q, W^k,W^v\)

最后，鉴于我们使用矩阵处理，将步骤 2~6 合并成一个计算 self-attention 层输出的公式。

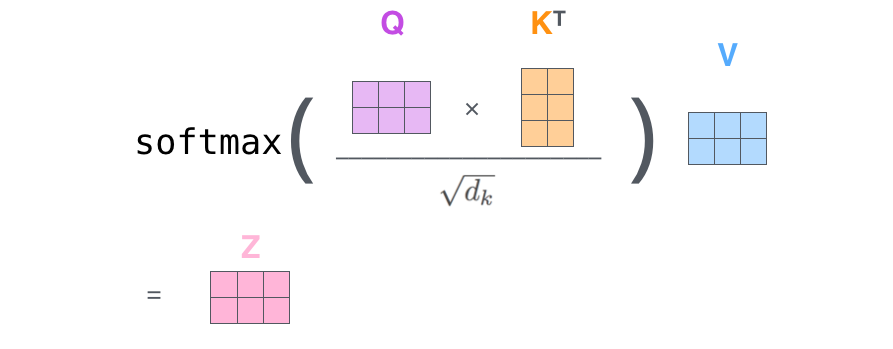
多头注意力机制

论文进一步增加了 multi-headed 的机制到 self-attention 上，在如下两个方面提高了 attention 层的效果：

1. 多头机制扩展了模型集中于不同位置的能力。在上面的例子中，z 1 只包含了其他词的很少信息，仅由实际自己词决定。在其他情况下，比如翻译 “The animal didn’t cross the street because it was too tired”时，我们想知道单词”it”指的是什么。
2. 多头机制赋予 attention 多种子表达方式。像下面的例子所示，在多头下有多组 query/key/value-matrix，而非仅仅一组（论文中使用 8-heads）。每一组都是随机初始化，经过训练之后，输入向量可以被映射到不同的子表达空间中。

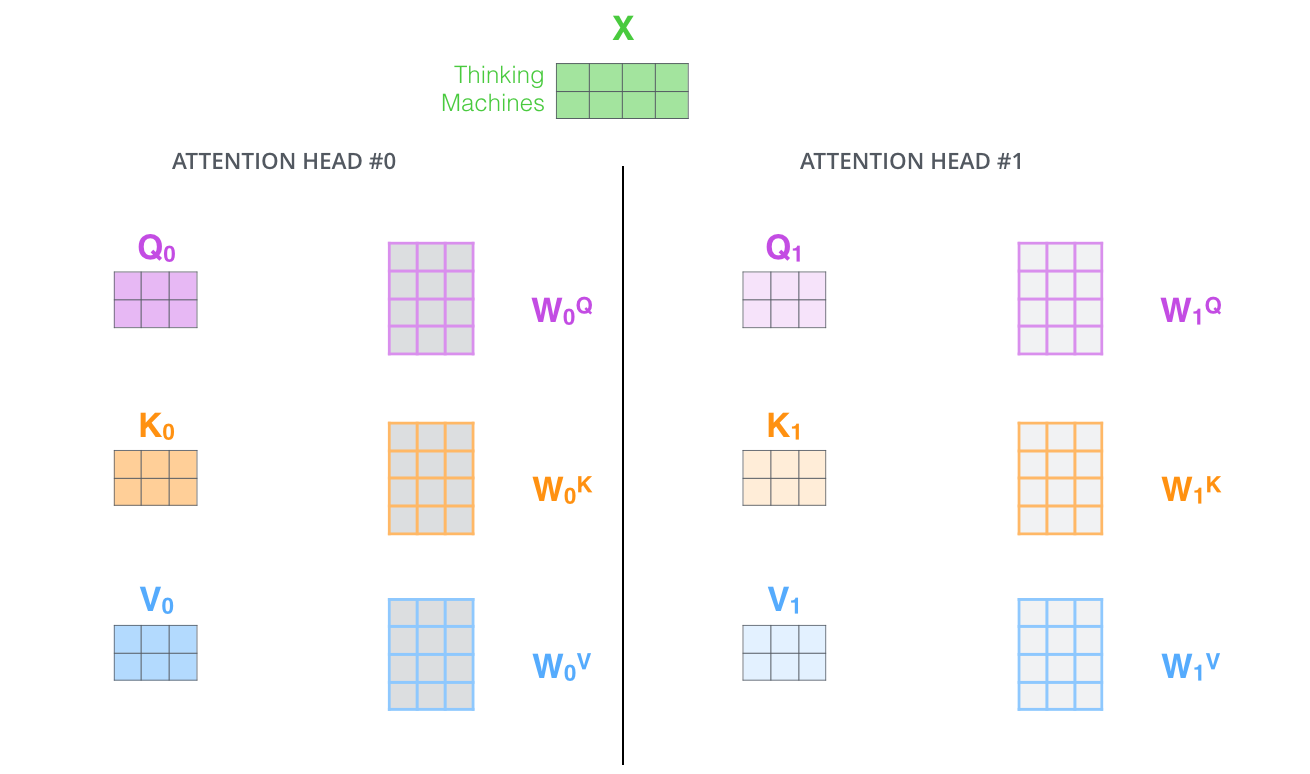如果我们计算 multi-headed self-attention 的，分别有八组不同的 Q/K/V matrix，我们得到八个不同的矩阵。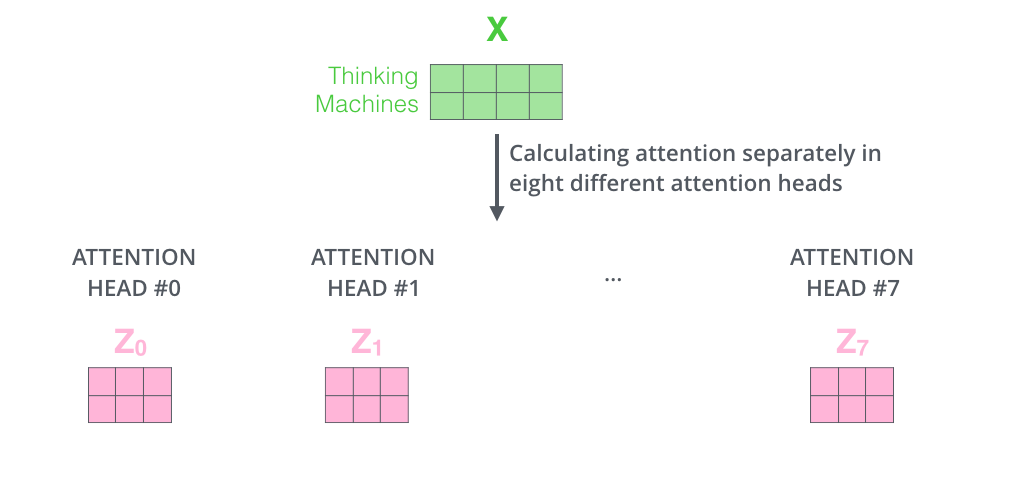

这会带来点麻烦，前向网络并不能接收八个矩阵，而是希望输入是一个矩阵，所以要有种方式处理下八个矩阵合并成一个矩阵。

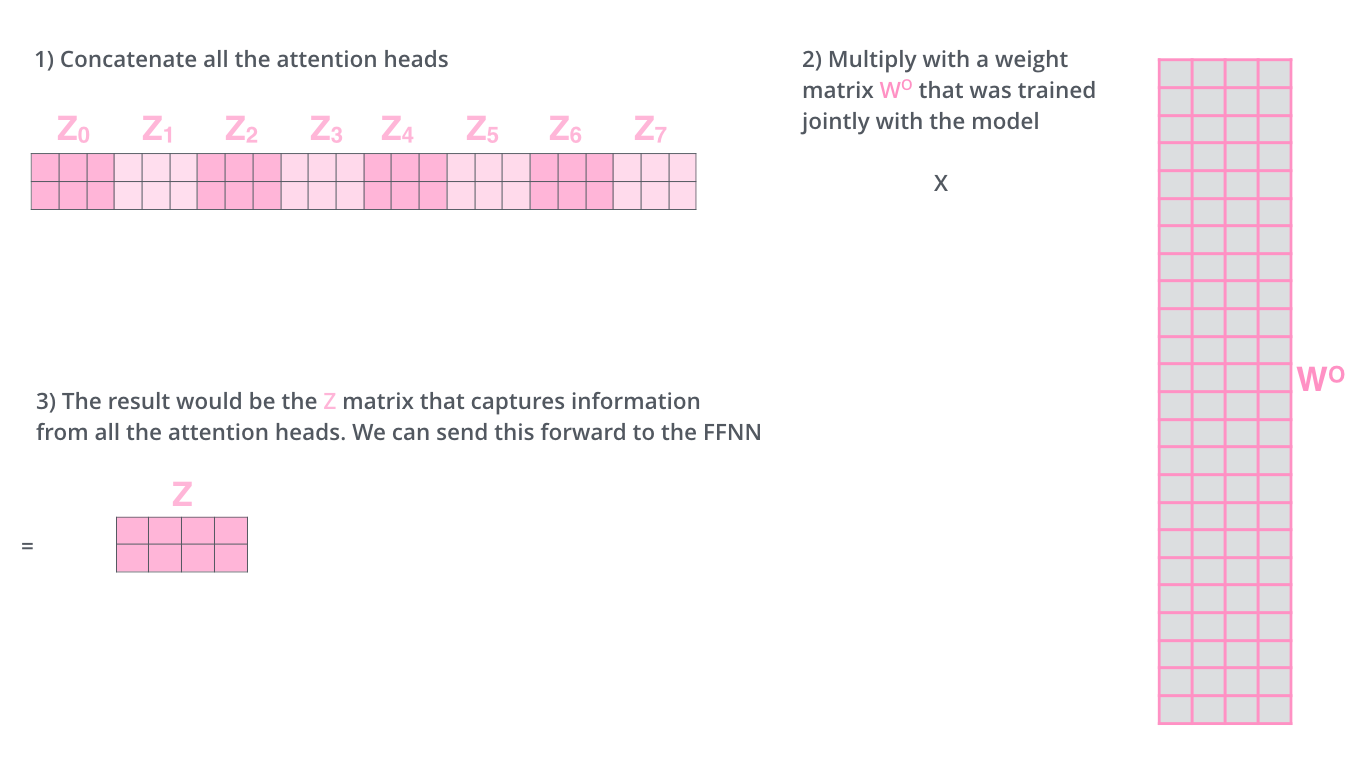
上述就是多头自注意机制的内容，我认为还仅是一部分矩阵，下面尝试着将它们放到一个图上可视化如下。

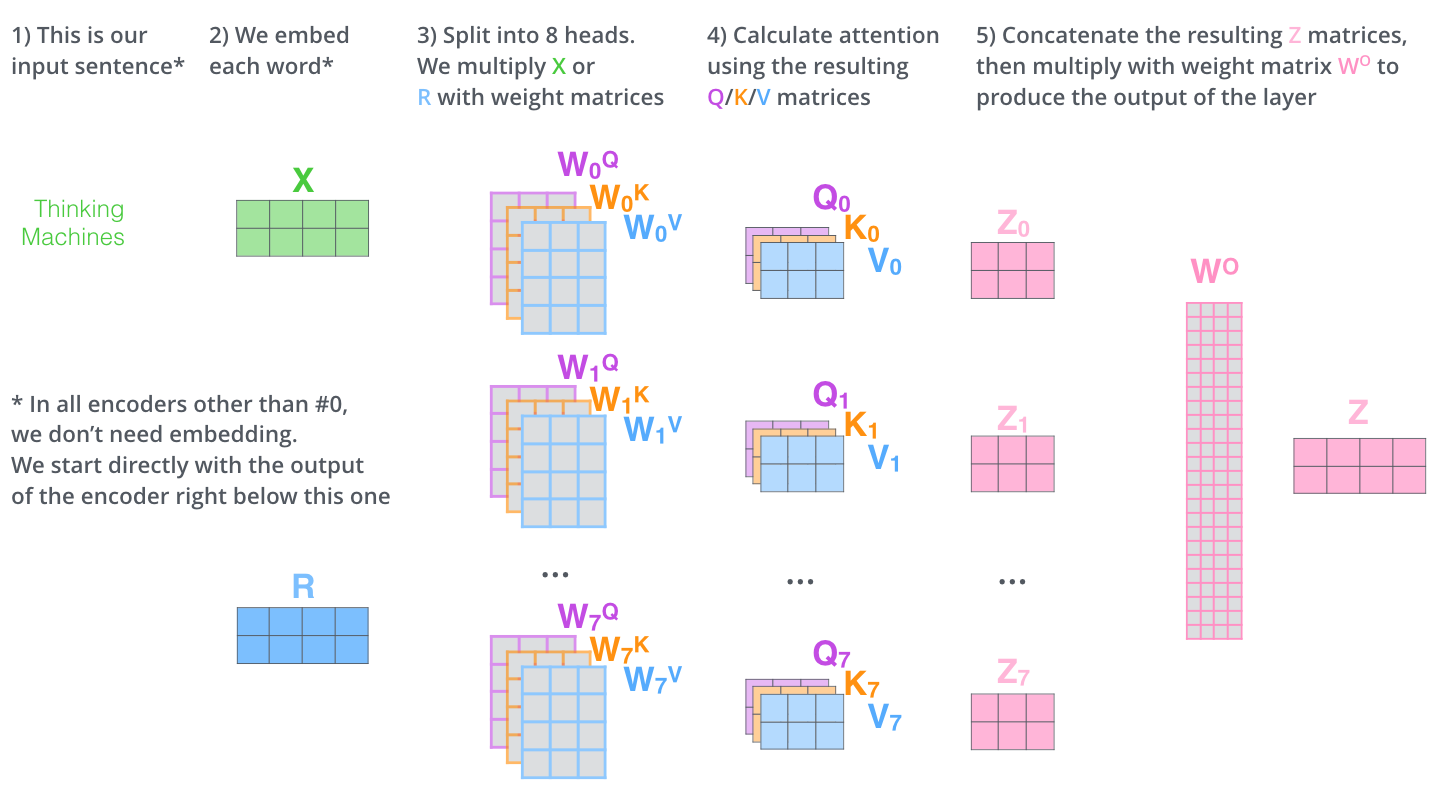#### 代码 下面实现一下多头注意力机制，在原论文中，实现的方法如下： 也就是对每个 W 进行多头的设置，即为原维度/head，然后拼接后，再经过 \(hd_v\times d_{model}\) 的转换又得到原来的维度，代码的实现不太一样，代码是 W 还是 \(d_{model}\times d_{model}\) 的矩阵然后得到 q, k, v 之后再进行截断，实现如下。

class MultiHeadedAttention(nn.Module):

    def __init__(self, h, d_model, dropout=0.1) -> None:

        # h为head，这里为8，d_model为embedding的维度，这里为512

        super().__init__()

        assert d_model % h == 0

        self.d_k = d_model // h # 64

        self.h = h

        self.Q_Linear = nn.Linear(d_model, d_model)

        self.K_Linear = nn.Linear(d_model, d_model)

        self.V_Linear = nn.Linear(d_model, d_model)

        self.res_Linear = nn.Linear(d_model, d_model)

        self.attn = None

        self.dropout = nn.Dropout(p=dropout)

    def forward(self, query, key, value, mask=None):

        if mask is not None:

            mask = mask.unsqueeze(1)

        batch_size = query.size(0)

        query = self.Q_Linear(query).view(batch_size, -1, self.h, self.d_k) # (batch_size, seq_len, h, d_k)即(batch_size, seq_len, 8, 64)

        query = query.transpose(1, 2) # (batch_size, h, seq_len, d_k)即(batch_size, 8, seq_len, 64)

        key = self.K_Linear(key).view(batch_size, -1, self.h, self.d_k).transpose(1, 2)

        value = self.V_Linear(value).view(batch_size, -1, self.h, self.d_k).transpose(1, 2)

        x, self.attn = attention(query, key, value, mask=mask, dropout=self.dropout) # x为(batch_size, h, seq_len, d_k)

        # attn为(batch_size, h, seq_len1, seq_len2)

        x = x.transpose(1, 2).contiguous().view(batch_size, -1, self.h * self.d_k)

        # (batch_size, h, seq_len, d_k) -> (batch_size, seq_len, h, d_k) -> (batch_size, seq_len, h * d_k) = (batch_size, seq_len, 512)

        return self.res_Linear(x)

Masked self-attention

在训练的时候，主要是消除后面的信息对预测的影响，因为 decoder 输入的是整个句子，也就是我们所谓的参考答案，而实际预测的时候就是预测后面的 token，用不到后面的 token，如果不 mask 掉，当前的 token 将看到“未来”，这不是我们想要的，因此必须要 mask 掉。

其实 decoder 里的 sequence mask 与 encoder 里的 padding mask 异曲同工，padding mask 其实很简单，就是为了使句子长度一致进行了 padding，而为了避免关注 padding 的位置，进行了 mask，具体的做法就是将这些位置的值变成负无穷，这样 softmax 之后就接近于 0 了。

而 sequence mask 思想也差不多：

假设现在解码器的输入”< s > who am i < e >“在分别乘上一个矩阵进行线性变换后得到了 Q、K、V，且 Q 与 K 作用后得到了注意力权重矩阵（此时还未进行 softmax 操作），如图 17 所示。

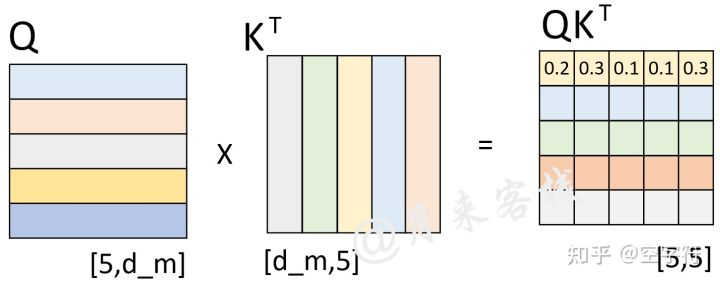
此时已经计算得到了注意力权重矩阵。由第 1 行的权重向量可知，在解码第 1 个时刻时应该将 20%（严格来说应该是经过 softmax 后的值）的注意力放到’< s >’上，30%的注意力放到’who’上等等。不过此时有一个问题就是，模型在实际的预测过程中只是将当前时刻之前（包括当前时刻）的所有时刻作为输入来预测下一个时刻，也就是说模型在预测时是看不到当前时刻之后的信息。因此，Transformer 中的 Decoder 通过加入注意力掩码机制来解决了这一问题。 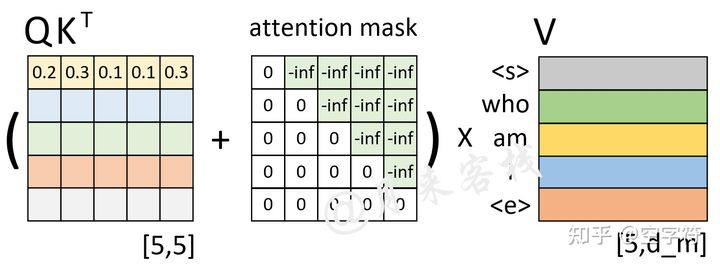当然还要进行 softmax 等计算。

在网上查了很多资料，说法都很不一样，不过我更倾向于这样的看法。而在预测的时候是用前面的输出结果作为输入的。

几张图帮助理解：

后面还有 padding mask，所有的 self attention 都要用这个，因为 pad 的位置没有任何意义。 实践一下加深理解： 首先我们来定义模型：

# 词典数为10， 词向量维度为8
embedding = nn.Embedding(10, 8)
# 定义Transformer，注意一定要改成eval模型，否则每次输出结果不一样
transformer = nn.Transformer(d_model=8, batch_first=True).eval()

接下来定义我们的 src 和 tgt：

# Encoder的输入
src = torch.LongTensor([[0, 1, 2, 3, 4]])
# Decoder的输入
tgt = torch.LongTensor([[4, 3, 2, 1, 0]])

然后我们将 [4] 送给 Transformer 进行预测，模拟推理时的第一步：

transformer(embedding(src), embedding(tgt[:, :1]),
            # 这个就是用来生成阶梯式的mask的
            tgt_mask=nn.Transformer.generate_square_subsequent_mask(1))

tensor([[[ 1.4053, -0.4680,  0.8110,  0.1218,  0.9668, -1.4539, -1.4427,
           0.0598]]], grad_fn=<NativeLayerNormBackward0>)

然后我们将 [4, 3] 送给 Transformer，模拟推理时的第二步：

transformer(embedding(src), embedding(tgt[:, :2]), tgt_mask=nn.Transformer.generate_square_subsequent_mask(2))

tensor([[[ 1.4053, -0.4680,  0.8110,  0.1218,  0.9668, -1.4539, -1.4427,
           0.0598],
         [ 1.2726, -0.3516,  0.6584,  0.3297,  1.1161, -1.4204, -1.5652,
          -0.0396]]], grad_fn=<NativeLayerNormBackward0>)

出的第一个向量和上面那个一模一样。

最后我们再将 tgt 一次性送给 transformer，模拟训练过程：

transformer(embedding(src), embedding(tgt), tgt_mask=nn.Transformer.generate_square_subsequent_mask(5))

tensor([[[ 1.4053, -0.4680,  0.8110,  0.1218,  0.9668, -1.4539, -1.4427,
           0.0598],
         [ 1.2726, -0.3516,  0.6584,  0.3297,  1.1161, -1.4204, -1.5652,
          -0.0396],
         [ 1.4799, -0.3575,  0.8310,  0.1642,  0.8811, -1.3140, -1.5643,
          -0.1204],
         [ 1.4359, -0.6524,  0.8377,  0.1742,  1.0521, -1.3222, -1.3799,
          -0.1454],
         [ 1.3465, -0.3771,  0.9107,  0.1636,  0.8627, -1.5061, -1.4732,
           0.0729]]], grad_fn=<NativeLayerNormBackward0>)

可以看到使用 mask 后就可以保证前面的结果都是不变的，不然如果没有 mask 则计算 attention 时因为计算注意力变化所以结果都会变化，这就是 Mask self-attention 的意义。 到这里 self-attention 就介绍完了