llama系列
LLaMA介绍
LLaMA 是目前为止,效果最好的开源 LLM 之一。
论文的核心思想:相比于GPT,更小的模型+更多的训练数据**也可以获得可比的效果
基于更多 tokens
的训练集,在各种推理预算下,训练出性能最佳的一系列语言模型,称为
LLaMA,参数范围从 7B 到 65B 不等,与现有最佳 LLM
相比,其性能是有竞争力的。比如,LLaMA-13B 在大多数基准测试中优于
GPT-3,尽管其尺寸只有 GPT-3 的十分之一。作者相信,LLaMA 将有助于使 LLM
的使用和研究平民化,因为它可以在单个 GPU
上运行!在规模较大的情况下,LLaMA-65B 也具有与最佳大型语言模型(如
Chinchilla 或 PaLM-540B)相竞争的能力。
LLaMA1、2的主要差别在训练上下文长度、训练token数、注意力机制以及对齐方法上。
| 模型 | 训练长度 | 分词器 | 词表大小 | 位置编码 | 激活层 | 标准化 | 训练token数 | 链接 | 精度 | 注意力机制 | 有无chat版本 | Alignment |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| LLaMA | 2,048 | BPE(Sentence-Piece) | 32k | ROPE | SwiGLU | 基于 RMSNorm 的 Pre-Norm | 1万亿(6.7B,13B) 1.4万亿(32.5B,65.2B) |
http://arxiv.org/abs/2302.13971 | fp16 | MHA | 0 | |
| LLaMA2 | 4,096 | 同上 | 32k | ROPE | 同上 | 同上 | 2万亿 | https://arxiv.org/abs/2307.09288 | bf16 | 34B,70B GQA, 其他MHA | 1 | SFT+RLHF(拒绝采样+PPO) |
(表来自LLaMA家族)
LLaMA1
训练数据
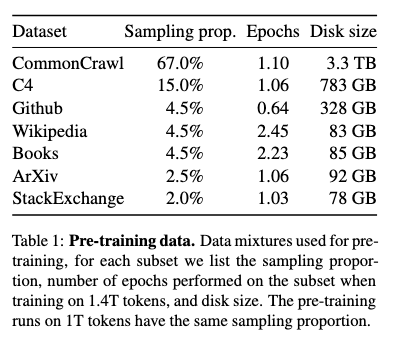
训练参数
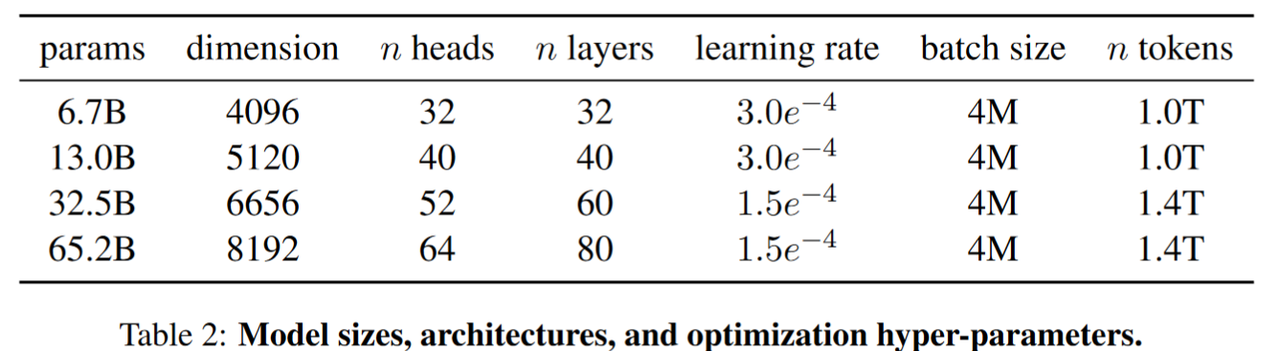
RMSnorm
与 Layer Norm 相比,RMS Norm的主要区别在于去掉了减去均值的部分,计算公式为:
\[\overline{a}_{i}=\frac{a_{i}}{RMS(a)}\]
其中
\[RMS(a)=\sqrt{\frac{1}{n}\Sigma_{i=1}^{n}a_{i}^{2}} \\ \]
此外RMSNorm 还可以引入可学习的缩放因子g,从而得到
\[\overline{a}_i=\frac{a_i}{RMS(\boldsymbol{a})}g_i\]
Pre-norm和Post-norm
注意其使用的是Pre-norm结构,与Post-norm结构差异如下: 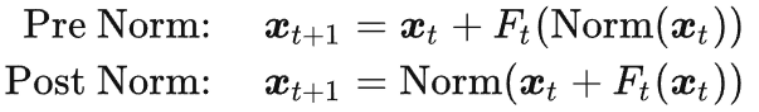
关于Pre Norm的效果和Post Norm效果差异,相关分析在这两篇文章中:
总结来说就是Pre-norm加深的是模型的宽度,而不是深度,从而导致训练效果不如Post-norm,但可以缓解Post-norm的梯度消失。
代码
class LlamaRMSNorm(nn.Module):
def __init__(self, hidden_size, eps=1e-6):
"""
LlamaRMSNorm is equivalent to T5LayerNorm
"""
super().__init__()
self.weight = nn.Parameter(torch.ones(hidden_size))
self.variance_epsilon = eps # eps 防止取倒数之后分母为0
def forward(self, hidden_states):
input_dtype = hidden_states.dtype
variance = hidden_states.to(torch.float32).pow(2).mean(-1, keepdim=True)
hidden_states = hidden_states * torch.rsqrt(variance + self.variance_epsilon) # rsqrt 即sqrt后取倒数
# weight 是末尾乘的可训练参数, 即g_i
return (self.weight * hidden_states).to(input_dtype)RoPE
RoPE 的核心思想是“通过绝对位置编码的方式实现相对位置编码”,可以说是具备了绝对位置编码的方便性,同时可以表示不同 token 之间的相对位置关系。RoPE 是将位置编码和 query或者key进行相乘。
\[\begin{bmatrix}\cos m\theta_0&-\sin m\theta_0&0&0&\cdots&0&0\\\sin m\theta_0&\cos m\theta_0&0&0&\cdots&0&0\\0&0&\cos m\theta_1&-\sin m\theta_1&\cdots&0&0\\0&0&\sin m\theta_1&\cos m\theta_1&\cdots&0&0\\\vdots&\vdots&\vdots&\vdots&\ddots&\vdots&\vdots\\0&0&0&0&\cdots&\cos m\theta_{d/2-1}&-\sin m\theta_{d/2-1}\\0&0&0&0&\cdots&\sin m\theta_{d/2-1}&\cos m\theta_{d/2-1}\end{bmatrix}\begin{bmatrix}q_0\\q_1\\q_2\\q_3\\\vdots\\q_{d-2}\\q_{d-1}\end{bmatrix}\]
由于矩阵太稀疏,会造成浪费,因此计算时是这么做的:
\[\begin{bmatrix}q_0\\q_1\\q_2\\q_3\\\vdots\\q_{d-2}\\q_{d-1}\end{bmatrix}\otimes\begin{bmatrix}\cos m\theta_0\\\cos m\theta_0\\\cos m\theta_1\\\cos m\theta_1\\\vdots\\\cos m\theta_{d/2-1}\\\cos m\theta_{d/2-1}\end{bmatrix}+\begin{bmatrix}-q_1\\q_0\\-q_3\\q_2\\\vdots\\-q_{d-1}\\q_{d-2}\end{bmatrix}\otimes\begin{bmatrix}\sin m\theta_0\\\sin m\theta_0\\\sin m\theta_1\\\sin m\theta_1\\\vdots\\\sin m\theta_{d/2-1}\\\sin m\theta_{d/2-1}\end{bmatrix}\]
此外,角度的计算方式如下:
\[\theta_j=10000^{-2j/d},j\in[1,2,\dots,d/2]\]
代码
class LlamaRotaryEmbedding(torch.nn.Module):
def __init__(self, dim, max_position_embeddings=2048, base=10000, device=None):
super().__init__()
inv_freq = 1.0 / (base ** (torch.arange(0, dim, 2).float().to(device) / dim))
self.register_buffer("inv_freq", inv_freq)
# Build here to make `torch.jit.trace` work.
self.max_seq_len_cached = max_position_embeddings
t = torch.arange(self.max_seq_len_cached, device=self.inv_freq.device,
dtype=self.inv_freq.dtype)
freqs = torch.einsum("i,j->ij", t, self.inv_freq)
# Different from paper, but it uses a different permutation
# in order to obtain the same calculation
emb = torch.cat((freqs, freqs), dim=-1)
dtype = torch.get_default_dtype()
self.register_buffer("cos_cached", emb.cos()[None, None, :, :].to(dtype), persistent=False)
self.register_buffer("sin_cached", emb.sin()[None, None, :, :].to(dtype), persistent=False)
def forward(self, x, seq_len=None):
# x: [bs, num_attention_heads, seq_len, head_size]
# This `if` block is unlikely to be run after we build sin/cos in `__init__`.
# Keep the logic here just in case.
if seq_len > self.max_seq_len_cached:
self.max_seq_len_cached = seq_len
t = torch.arange(self.max_seq_len_cached, device=x.device, dtype=self.inv_freq.dtype)
freqs = torch.einsum("i,j->ij", t, self.inv_freq)
# Different from paper, but it uses a different permutation
# in order to obtain the same calculation
emb = torch.cat((freqs, freqs), dim=-1).to(x.device)
self.register_buffer("cos_cached", emb.cos()[None, None, :, :].to(x.dtype),
persistent=False)
self.register_buffer("sin_cached", emb.sin()[None, None, :, :].to(x.dtype),
persistent=False)
return (
self.cos_cached[:, :, :seq_len, ...].to(dtype=x.dtype),
self.sin_cached[:, :, :seq_len, ...].to(dtype=x.dtype),
)
def rotate_half(x):
"""Rotates half the hidden dims of the input."""
x1 = x[..., : x.shape[-1] // 2]
x2 = x[..., x.shape[-1] // 2 :]
return torch.cat((-x2, x1), dim=-1)
def apply_rotary_pos_emb(q, k, cos, sin, position_ids):
# The first two dimensions of cos and sin are always 1, so we can `squeeze` them.
cos = cos.squeeze(1).squeeze(0) # [seq_len, dim]
sin = sin.squeeze(1).squeeze(0) # [seq_len, dim]
cos = cos[position_ids].unsqueeze(1) # [bs, 1, seq_len, dim]
sin = sin[position_ids].unsqueeze(1) # [bs, 1, seq_len, dim]
q_embed = (q * cos) + (rotate_half(q) * sin)
k_embed = (k * cos) + (rotate_half(k) * sin)
return q_embed, k_embedSwiGLU
\[\begin{aligned} \mathrm{FFN}_{\mathrm{SwiGLU}}(x,W,V,W_{2})&=\mathrm{SwiGLU}(x,W,V)W_{2}\\\mathrm{SwiGLU}(x,W,V)&=\mathrm{Swish}_{\beta}(xW)\otimes xV\\\mathrm{Swish}_{\beta}(x)&=x\sigma(\beta x) \end{aligned}\]
代码
class LlamaMLP(nn.Module):
def __init__(
self,
hidden_size: int,
intermediate_size: int,
hidden_act: str,
):
super().__init__()
self.gate_proj = nn.Linear(hidden_size, intermediate_size, bias=False)
self.down_proj = nn.Linear(intermediate_size, hidden_size, bias=False)
self.up_proj = nn.Linear(hidden_size, intermediate_size, bias=False)
# config 中 hidden_act = 'silu'
# 'silu' 和 'swish' 对应的激活函数均为:SiLUActivation
# https://github.com/huggingface/transformers/blob/717dadc6f36be9f50abc66adfd918f9b0e6e3502/src/transformers/activations.py#L229
self.act_fn = ACT2FN[hidden_act]
def forward(self, x):
# 对应上述公式的 SwiGLU
return self.down_proj(self.act_fn(self.gate_proj(x)) * self.up_proj(x))实验结果
常识推理任务
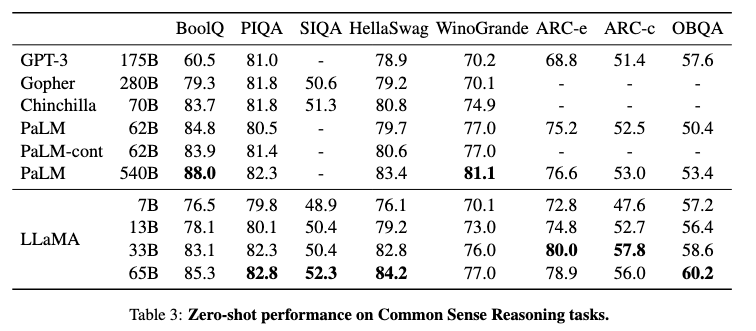
- LLaMA - 13B模型虽然比GPT - 3小10倍,但在大多数基准上也优于GPT - 3。
- 除BoolQ外,LLaMA - 65B在所有报告的基准上都优于Chinchilla-70B。
- 除了在BoolQ和WinoGrande上,LLaMA-65B在所有地方都超过了PaLM540B。
阅读理解任务
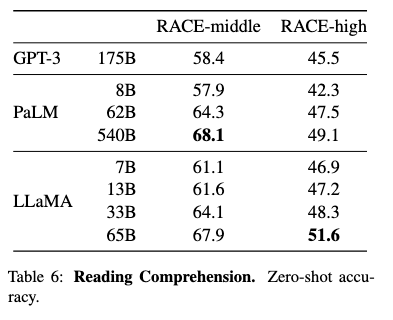
- 可以看到,LLaMA-13B比GPT-3高出了几个百分点。
- LLaMA-65B的表现已经接近甚至超越PaLM-540B的表现。
LLaMA2
Llama1只做了预训练,Llama2做了预训练+SFT+RLHF 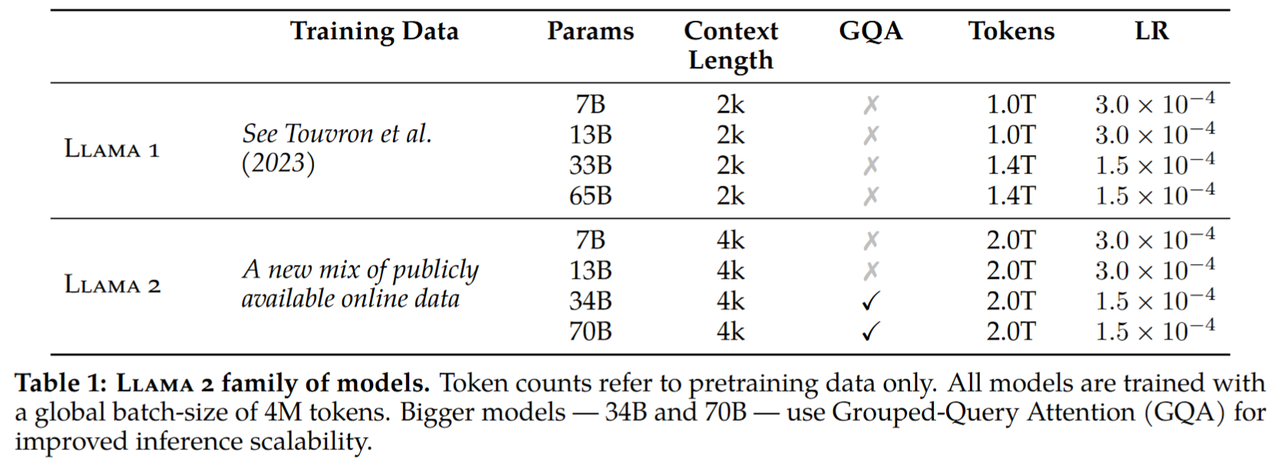
KV Cache
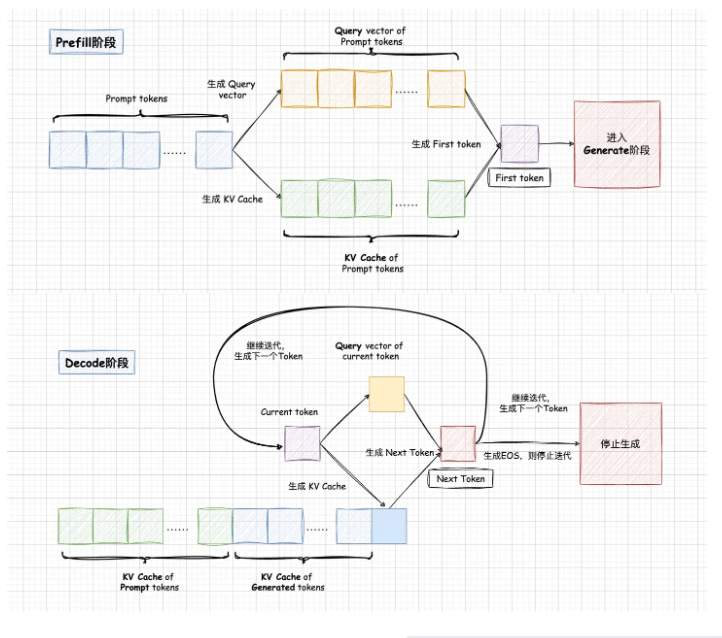
LLM推理过程分为Prefill和Decode两个阶段。
- Prefill阶段会对Prompt中所有的token做
并行计算,得到Prompt中所有Tokens的KV Cache以及计算得到生成的第一个Token。Prompt阶段Token计算得到的KV Cache会保存下来,留给Decode阶段复用。 - Decode阶段是一个自回归过程,每decode一个新的Token,都需要用到所有之前计算得到的KV Cache来计算当前query token的Attention。因此,当输出长度越来越大或者context很长时,KV Cache将会占用大量的显存。
使用KV cache时位置信息怎么注入?
初次学习KV cache时,虽然原理比较简单易懂,但是对于后续的输入只有一个token这里产生了些许困惑,后续只输入一个token的话,位置编码该怎么办呢?于是我比较简单粗暴地猜测位置index随着推理不断更新,当时翻了各种资料也没有得到解释,后面翻了翻llama的源码,发现我的猜测还真是正确的。
def forward(self, tokens: torch.Tensor, start_pos: int):
"""
Perform a forward pass through the Transformer model.
Args:
tokens (torch.Tensor): Input token indices.
start_pos (int): Starting position for attention caching.
Returns:
torch.Tensor: Output logits after applying the Transformer model.
"""
_bsz, seqlen = tokens.shape
h = self.tok_embeddings(tokens)
self.freqs_cis = self.freqs_cis.to(h.device)
freqs_cis = self.freqs_cis[start_pos : start_pos + seqlen]
mask = None
if seqlen > 1:
mask = torch.full(
(seqlen, seqlen), float("-inf"), device=tokens.device
)
mask = torch.triu(mask, diagonal=1)
# When performing key-value caching, we compute the attention scores
# only for the new sequence. Thus, the matrix of scores is of size
# (seqlen, cache_len + seqlen), and the only masked entries are (i, j) for
# j > cache_len + i, since row i corresponds to token cache_len + i.
mask = torch.hstack([
torch.zeros((seqlen, start_pos), device=tokens.device),
mask
]).type_as(h)
for layer in self.layers:
h = layer(h, start_pos, freqs_cis, mask)
h = self.norm(h)
output = self.output(h).float()
return output可以看到forward函数中的start_pos参数代表着位置信息,freqs_cis是实现RoPE位置编码需要用到的。
注意
freqs_cis = self.freqs_cis[start_pos : start_pos + seqlen]这一行,即是实现了rope相对位置编码的kv
cache的核心。
代码
class Attention(nn.Module):
# ...
self.cache_k = torch.zeros(
(
args.max_batch_size,
args.max_seq_len,
self.n_local_kv_heads,
self.head_dim,
)
).cuda()
self.cache_v = torch.zeros(
(
args.max_batch_size,
args.max_seq_len,
self.n_local_kv_heads,
self.head_dim,
)
).cuda()
def forward(
self,
x: torch.Tensor,
start_pos: int,
freqs_cis: torch.Tensor,
mask: Optional[torch.Tensor],
):
# 假设当前x为(1, 1, dim),也就是上一个预测的token
# self-attention的输入,标准的(bs, seqlen, hidden_dim)
bsz, seqlen, _ = x.shape
# 计算当前token的qkv
# q k v分别进行映射,注意这里key, value也需要先由输入进行映射再和kv_cache里面的key, value进行拼接
xq, xk, xv = self.wq(x), self.wk(x), self.wv(x)
xq = xq.view(bsz, seqlen, self.n_local_heads, self.head_dim)
xk = xk.view(bsz, seqlen, self.n_local_kv_heads, self.head_dim)
xv = xv.view(bsz, seqlen, self.n_local_kv_heads, self.head_dim)
# 对当前输入的query和key进行RoPE,注意kv_cache里面的key已经做过了RoPE
xq, xk = apply_rotary_emb(xq, xk, freqs_cis=freqs_cis)
# 缓存当前token的kv
self.cache_k = self.cache_k.to(xq)
self.cache_v = self.cache_v.to(xq)
self.cache_k[:bsz, start_pos: start_pos + seqlen] = xk
self.cache_v[:bsz, start_pos: start_pos + seqlen] = xv
# 取出前seqlen个token的kv缓存
# 取出全部缓存的key和value(包括之前在cache里面的和本次输入的),作为最终的key和value
keys = self.cache_k[:bsz, : start_pos + seqlen]
values = self.cache_v[:bsz, : start_pos + seqlen]
# 将kv重复填充,使kv和q的头数个数相同
# repeat k/v heads if n_kv_heads < n_heads,对齐头的数量
keys = repeat_kv(keys, self.n_rep) # (bs, cache_len + seqlen, n_local_heads, head_dim)
values = repeat_kv(values, self.n_rep) # (bs, cache_len + seqlen, n_local_heads, head_dim)
# 计算当前token的attention score,,注意mask需要加上,另外维度要对应上
xq = xq.transpose(1, 2) # (bs, n_local_heads, seqlen, head_dim)
keys = keys.transpose(1, 2) # (bs, n_local_heads, cache_len + seqlen, head_dim)
values = values.transpose(1, 2) # (bs, n_local_heads, cache_len + seqlen, head_dim)
scores = torch.matmul(xq, keys.transpose(2, 3)) / math.sqrt(self.head_dim)
if mask is not None:
scores = scores + mask # (bs, n_local_heads, seqlen, cache_len + seqlen)
scores = F.softmax(scores.float(), dim=-1).type_as(xq)
output = torch.matmul(scores, values) # (bs, n_local_heads, seqlen, head_dim)
output = output.transpose(1, 2).contiguous().view(bsz, seqlen, -1)
return self.wo(output)MQA&GQA
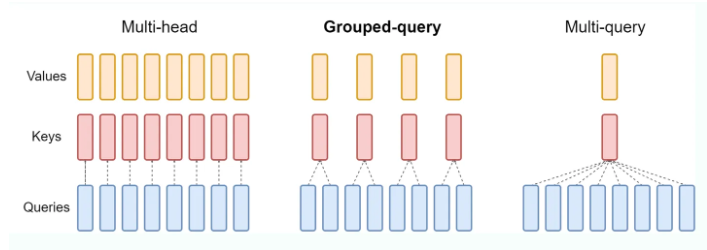
为什么不继续使用MHA?
- 标准的mha中,KV heads的数量和Query heads的数量相同,每一个q head对应一个独立的kv head,但这样的开销比较大。
MQA
标准的MHA中,KV heads的数量和Query heads的数量相同,每一个q head对应一个独立的kv head,但这样的开销比较大。
MQA比较极端,只保留一个KV Head,多个Query Heads共享相同的KV Head。这相当于不同Head的Attention差异,全部都放在了Query上,需要模型仅从不同的Query Heads上就能够关注到输入hidden states不同方面的信息。这样做的好处是,极大地降低了KV Cache的需求,但是会导致模型效果有所下降。
GQA
- GQA就是在MHA和MQA之间做了一个平衡。对query heads进行分组,分成几组就对应多少个kv heads,然后每一组内的query Heads共享相同的KV head。
- GQA可以在减少计算量和KV Cache同时确保模型效果不受到大的影响。
SFT
监督微调(Supervised Fine-Tuning, SFT)是对已经预训练的模型进行特定任务的训练,以提高其在该任务上的表现。预训练模型通常在大量通用数据上进行训练,学到广泛的语言知识和特征。在SFT过程中,利用特定任务的数据,对模型进行进一步调整,使其更适合该任务。
SFT数据一般就是<prompt, response>数据对。在训练方式上和pretrain没有任何区别,即得到当前token对应的logit,以next token作为标签计算交叉熵损失。
pretrain 是在背书,纯粹的学习知识;sft 则是在做题,学习的是指令 follow 能力。
一些要点
少量高质量数据集训练模型的效果,要好于大量低质量数据集的训练效果。分析数据和清洗数据就是 sft 阶段 90% 的工作量。
sft 会让模型见到最重要的 eos_token,pretrain 模型因为没见过该 token 而无法停止生成。
sft 的 prompt 不做 loss,但这并不是说它不能做 loss。主要原因是 prompt 的同质化比较严重,不做 loss_mask 的话,同样的一句话会被翻来覆去的学,但如果你能保证你的每条 prompt 都是独一无二的,就完全可以省去 prompt 的 loss_mask 环节。
为了提高模型训练效率,将多组数据进行拼接,尽量填满4096。但对于分类任务会出现问题,详见https://zhuanlan.zhihu.com/p/809229182。
经过一通分析后,我们发现,新的训练方式改变了短 answer 数据的 loss 占比,毕竟模型在计算 loss 的时候,是先算一个句子内每个 token 的 平均 loss,再算一个 batch_size 内的平均 loss。
分类任务的 answer 通常只有 1 个 token:不 concat 的时候,它的 loss 贡献就是 1 / batch_size;concat 的时候,它就需要先和别的 answer 的 token 算平均 loss,再贡献 1 / batch_size。
这也就是说,采用 llama2 提到的 先 concat 语料再做 sft 训练,会对短 answer 数据很不公平,也就更容易造成短 answer 数据的欠拟合,pretrain 由于所有 token 都算 loss 则没有这个现象。最终,我们通过上采样短 answer 数据,成功的避免了分类任务的效果下滑。
实验结果
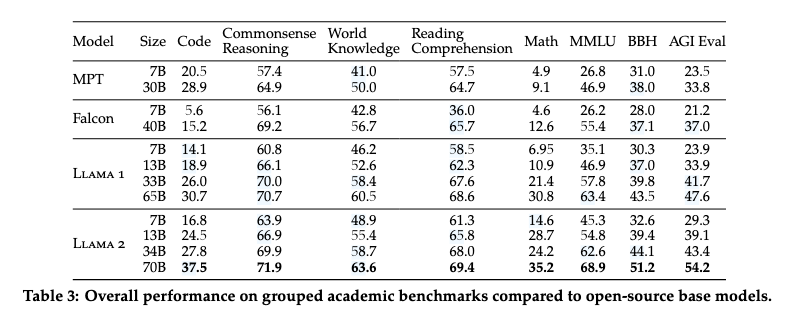 - Llama 2模型优于Llama 1模型。 - Llama 2-70B比Llama
1-65B在MMLU和BBH上的结果分别提高了≈5和≈8个点。 - Llama
2-7B和30B模型在除代码基准以外的所有类别上都优于相应大小的MPT模型。 -
Llama 2-7B和34B在所有类别的基准测试集上都优于Falcon-7B和40B模型。
- Llama 2模型优于Llama 1模型。 - Llama 2-70B比Llama
1-65B在MMLU和BBH上的结果分别提高了≈5和≈8个点。 - Llama
2-7B和30B模型在除代码基准以外的所有类别上都优于相应大小的MPT模型。 -
Llama 2-7B和34B在所有类别的基准测试集上都优于Falcon-7B和40B模型。
参考
- [KV Cache优化]🔥MQA/GQA/YOCO/CLA/MLKV笔记: 层内和层间KV Cache共享 - 知乎 (zhihu.com)
- Transformers KV Caching Explained | by João Lages | Medium
- https://zhuanlan.zhihu.com/p/679640407
- LLaMA家族
- https://zhuanlan.zhihu.com/p/809229182