pre-norm

Pre-norm:\(X_t+1=X_{t}+F_{t}(Norm(X_{t}))\)

\(先来看Pre-norm^{+},递归展开：\) \[X_{t+1}=X_t+F_t(Norm(X_t))\] \(=X_{0}+F_{1}(Norm(X_{1}))+\ldots+F_{t-1}(Norm(X_{t-1}))+F_{t}(Norm(X_{t}))\) 其中，展开\(^{+}\)后的每一项( \(F_{1}( Norm( X_{1}) ) , \ldots\), \(F_{t- 1}( Norm( X_{t- 1}) )\), \(F_{t}( Norm( X_{t}) )\))之间都是同一量级的， 所以\(F_1(Norm(X_1))+\ldots F_{t-1}(Norm(X_{t-1}))+F_t(Norm(X_t))\)和 \(F_1(Norm(X_1))+\ldots F_{t-1}(Norm(X_{t-1}))\)之间的区别就像t和t-1的区别一样，我们可以将 其记为\(X_t+ 1= \mathscr{O} ( t+ 1)\) . 这种特性就导致当t足够大的时候，\(X_{t+1}\)和\(X_t\)之间区别可以忽略不计（直觉上），那么就有：

\[F_t(X_t)+F_{t+1}(X_{t+1})\approx F_t(X_t)+F_{t+1}(X_t)=(F_t\bigoplus F_{t+1})(X_t)\] 这就是所谓的增加宽度，而没有增加深度。从而导致pre-norm的精度不高。 # post-norm

Post-norm:\(X_{t+1}=Norm(X_{t}+F_{t}(x_{t}))\) 本来layernorm是为了缓解梯度消失，但是在post-norm这里却成为了梯度消失的罪魁祸首。也导致了收敛较难、需要大量调参。

\[X_{t+1}=Norm(X_t+F_t(X_t))=\frac{X_t+F_t(X_t)}{\sqrt{2}}\] \[=\frac{X_0}{\sqrt{2}^{t+1}}+\frac{F_0(X_0)}{\sqrt{2}^{t+1}}+\ldots+\frac{F_{t-1}(X_{t-1})}{\sqrt{2}^2}+\frac{F_t(X_t)}{\sqrt{2}}\:(\] 这个结构跟pre-norm比起来充分考虑了所有分支 (残差\(^{+})\) 的输出，做到了真正增加深度，自然精度会相对好一些。

不过它也有它很显然的问题，当t足够大、也就是叠加的attention层足够多以后，底层那些分支(残差)的影响力被衰减掉了，残差有利于解决梯度消失，但是在Post Norm中，残差这条通道被严重削弱了，越靠近输入，削弱得越严重，残差“名存实亡”，那么势必会有梯度消失的问题，这也就是文章开头所说的postnorm难收敛、参数难调的原因。本来我们做Norm也是为了处理梯度消失，但从分析看来，transformer结构中的layernorm\(^{+}\)并没有完全实现它的作用。那这就意味着transformer原始结构的失败吗？并不是的，因为这种梯度消失的问题在整个结构上来看(配合上adam系优化器和学习率warmup，warmup对于post-norm极为重要) 是并不明显的。

离输入层的残差影响力弱这一特性，也有它的用武之地，比如在finetune的时候，我们就希望不要过多调整靠近输入层的参数、以免破坏预训练的效果。

warmup的重要性

Post-LN Transformer在训练的初始阶段，输出层附近的期望梯度非常大，所以，如果没有warm-up，模型优化过程就会炸裂，非常不稳定。 模型对越靠后的层越敏感，也就是越靠后的层学习得越快，然后后面的层是以前面的层的输出为输入的，前面的层根本就没学好，所以后面的层虽然学得快，但却是建立在糟糕的输入基础上的。 很快地，后面的层以糟糕的输入为基础到达了一个糟糕的局部最优点，此时它的学习开始放缓（因为已经到达了它认为的最优点附近），同时反向传播给前面层的梯度信号进一步变弱，这就导致了前面的层的梯度变得不准。但 Adam 的更新量是常数量级的，梯度不准，但更新量依然是常数量级，意味着可能就是一个常数量级的随机噪声了，于是学习方向开始不合理，前面的输出开始崩盘，导致后面的层也一并崩盘。

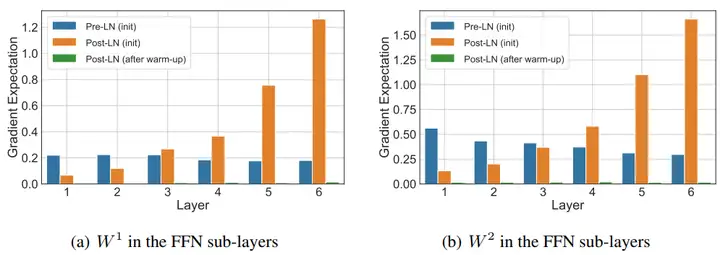
从上图中就可以看出来，post-ln在开始阶段层数越高梯度越大，此时需要小学习率，而当warmup完后，梯度变得很小（绿色部分）。此时可以使用大学习率。

Adam如何缓解梯度消失

其实。最关键的原因是，在当前的各种自适应优化技术“下，我们已经不大担心梯度消失问题了。这是因为，当前 NLP 中主流的优化器是 Adam 及其变种。对于 Adam 来说，由于包含了动量和二阶矩校正，所以近似来看，它的更新量大致上为 \[\Delta\theta=-\eta\frac{\mathbb{E}_{t}[g_{t}]}{\sqrt{\mathbb{E}_{t}[g_{t}^{2}]}}\] 可以看到，分子分母是都是同量纲的，因此分式结果其实就是 (1)的量级，而更新量就是 (n)量级。也就是说，理论上只要梯度的绝对值大于随机误差，那么对应的参数都会有常数量级的更新量（意思就是参数的更新量与梯度的关系不是很大，因此受梯度消失影响较小）；这跟 SGD 不一样，SGD 的更新量是正比于梯度的，只要梯度小，更新量也会很小，如果梯度 过小，那么参数几乎会没被更新。 所以，Post Norm 的残差虽然被严重削弱，但是在 base、large 级别的模型中，它还不至于削弱到小于随机误差的地步，因此配合 Adam 等优化器，它还是可以得到有效更新的，也就有可能成功训练了。当然，只是有可能，事实上越深的 Post Norm 模型确实越难训练，比如要仔细调节学习率和 Warmup 等。 # Deep-norm

\(最后再提一下DeepNet中结合Post-LN^+的良好性能以及Pre-LN的训练稳定性做出的改良\)。 \[X_{t+1}=Norm(\alpha X_t+F_t(X_t))\text{(6)}\] \(它在add norm之前给输入乘了一个up-scale^+的常数系数 α>1\)。

现在 (5) 的展开为： \[X_{t+1}=\frac{\alpha^{t+1}X_{0}}{\sqrt{2}^{t+1}}+\frac{\alpha^{t}F_{0}(X_{0})}{\sqrt{2}^{t+1}}+\ldots+\frac{\alpha F_{t-1}(X_{t-1})}{\sqrt{2}^{2}}+\frac{F_{t}(X_{t})}{\sqrt{2}}\] 因为\(\alpha>1\) ,所以它能够在保留post-norm真正增加了深度这优点的同时，一定程度避免了梯度

消失。（本质还是post-norm）

参考

Transformer梳理（一）：Post-Norm VS Pre-Norm - 知乎 (zhihu.com) 模型优化漫谈：BERT的初始标准差为什么是0.02？ - 科学空间|Scientific Spaces (kexue.fm) 为什么Pre Norm的效果不如Post Norm？ - 科学空间|Scientific Spaces (kexue.fm) 香侬读 | Transformer中warm-up和LayerNorm的重要性探究 - 知乎 (zhihu.com) Bert/Transformer 被忽视的细节（或许可以用来做面试题） - 知乎 (zhihu.com)