vllbc02KMP
KMP是字符串匹配问题的算法。“字符串A是否为字符串B的子串?如果是的话出现在B的哪些位置?”该问题就是字符串匹配问题，字符串A称为模式串，字符串B称为主串。
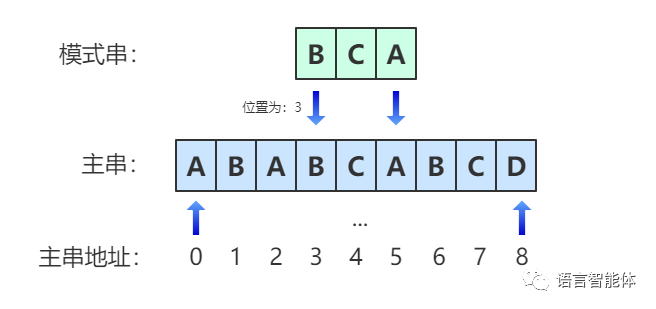
## BF算法
BF算法就是暴力匹配，即对主串从头开始慢慢移动模式串，直到找到相匹配的位置。
代码很简单暴力：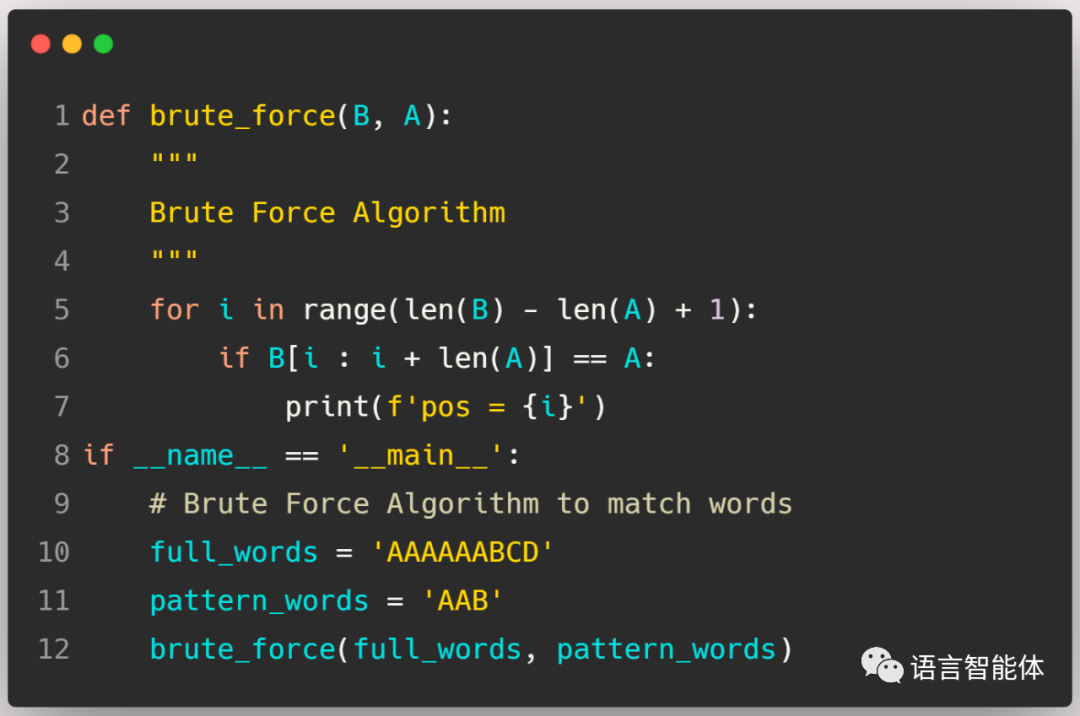 
假设n为主串长度，m为模式串长度。
每一轮字符串比较：最差的情况为模式串最后一个字与主串不同其他都相同（如模式串为AAB，主串对应部分为AAC），必须走完整个字符串才能得出结果，因此复杂度为O(m)。
所有轮字符串比较：最差的情况是移动到最后一次比较才寻找得到，总共需要n-m+1次，主串通常比模式串长很多，故Brute-Force时间复杂度为O(nm)
在匹配上没有办法进行优化，因此可以从模式串的移动上入手，由此引入了Kmp算法。
KMP
KMP 算法的不同之处在于，它会花费空间来记录一些信息。目的就是为了减少匹配的趟数，算法的核心就是每次匹配过程中推断出后续完全不可能匹配成功的匹配过程，从而减少比较的趟数。
Next数组
next数组实质上就是找出模式串中前后字符重复出现的个数，为了能够跳跃不可能匹配的步骤。 next数组的定义为：next[i]表示模式串A[0]至A[i]这个字串，使得前k个字符等于后k个字符的最大值，特别的k不能取i+i,因为字串一共才i+1个字符，自己跟自己相等毫无意义。
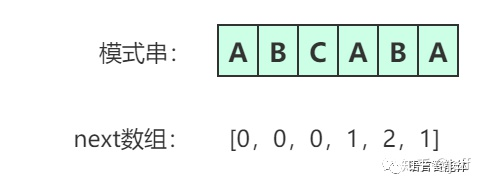
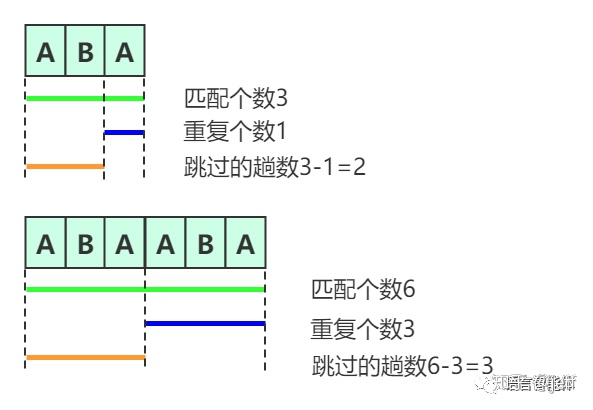
如何确定在移动过程中需要跳过多少步呢？下图更直观的体现了跳跃的过程：
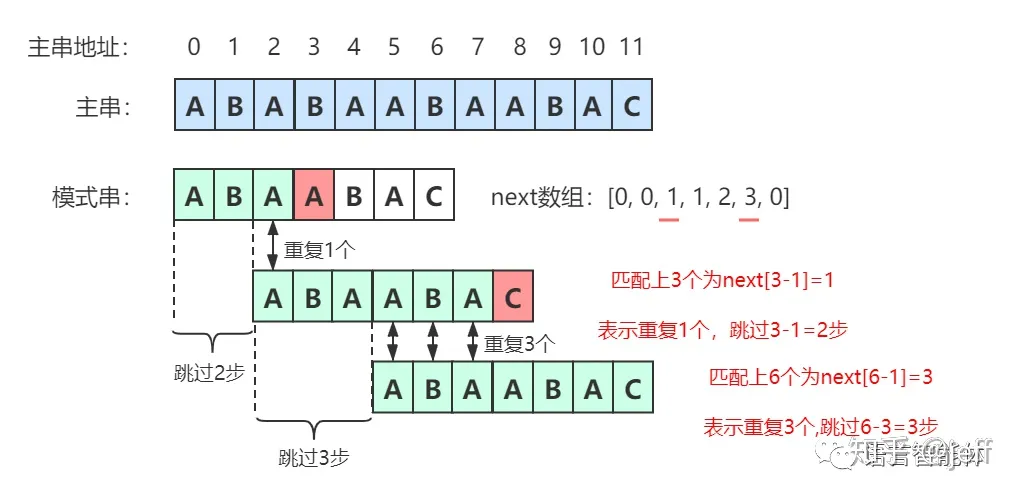也就是跳到模式串中的后缀相同字符串开始。因为这时可以确定前面的字符串肯定无法匹配了，过的趟数=匹配上字符串中间字符长度-重复字符串长度
在实际代码编写中，移动的实际上是模式串的匹配位置。前面展示的只是理解减小匹配次数这一过程。实际上跳动就是模式串比较指针的移动。模式串向右移动也就是比较指针向左移动，移动的距离就是跳过的趟数 移动后的指针为：\(j=j-(j-next[j-1]) =next[j-1]\) 其中原来的j为匹配成功的字符串长度，也就是匹配失败的指针位置。next[j-1]就是匹配成功的字符串的最长相同前后缀数，也就是要跳转到的指针的下标。（下标从0开始的，如果下标从1开始则在原来基础上+1就是要跳转到的位置，这也是为什么书上要+1）。
即下图所示。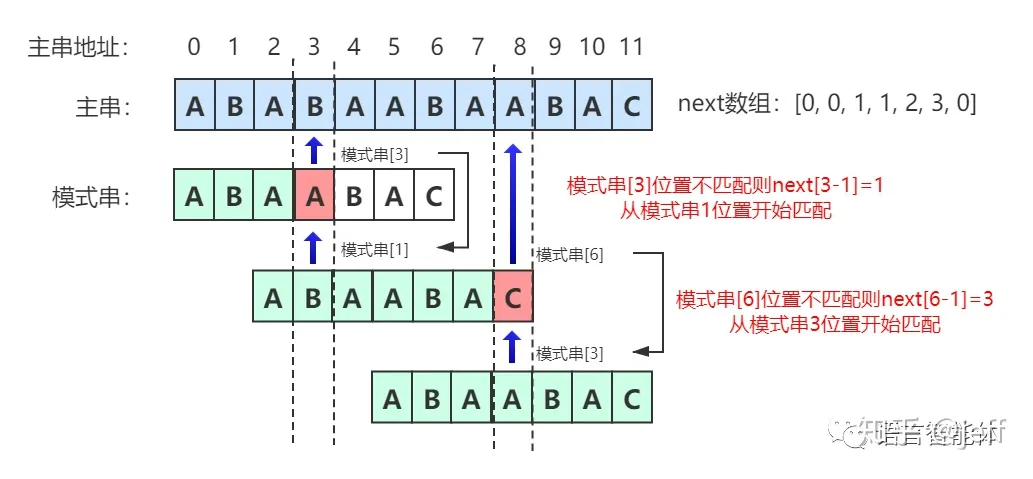 
然后再用移动后的指针和主串的上一轮匹配错误的位置相比，这时已经保证了前面的字符已经匹配了，即当前指针前面的子串已经和上一轮匹配成功的子串的最长后缀相同了。
因此可以看到，Kmp算法的核心就是构造Next数组。
最简单的方法就是根据定义暴力构造时间复杂度为O(m2法)：：
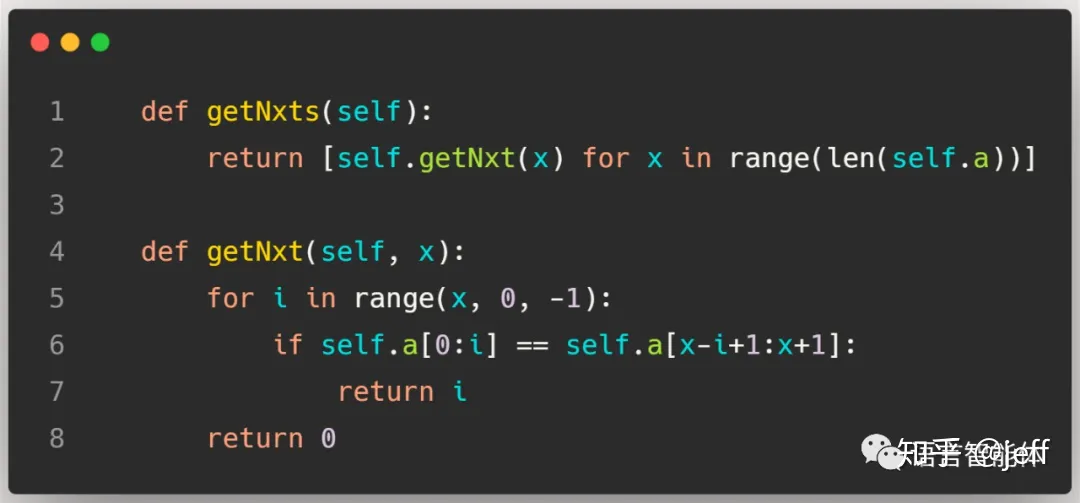
第二种构建方案，是一种递推的方式进行构建，时间复杂度为O(n+m):
考虑：如果next[0], next[1], … next[x-1]均已知，那么如何求出 next[x]
？我们已经知道next[x-1],标记next[x-1]=temp,则可以讨论A[temp]和A[x]的值，分2种情况讨论：
第一种情况：A[temp]等于A[x]，也就是说在前一个next结果上又多了一个字符串相同的长度，因此next[x]为next[x-1]+1
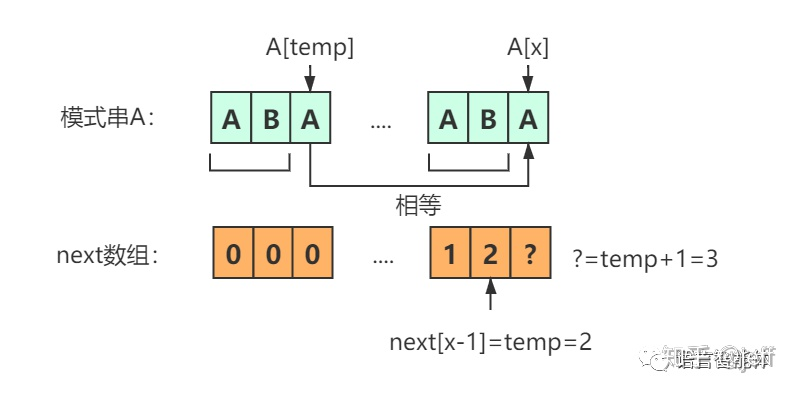这种情况说明了x-1时最长前缀的后一位和x位置的字符相同，则说明了前缀和后缀都增加了相同的1位，next[x]
= next[x-1] + 1。
（这里给一下我自己的理解，因为next中保存的是前后缀最大相同的长度，因此通常代表着最大相同前缀的后一位）
第二种情况：当A[temp]和A[x]不相等的时候，我们需要缩小temp,把temp变成next[temp-1]，直到A[temp]=A[x]为止。A[now]=A[x]时，就可以直接向右扩展了。
如何理解这张图，当发现A[temp] != A[x]的时候，就一直缩小temp，也就是temp
=
next[temp-1]，也就是找原来的最长前缀中对应的next[temp-1]，因为前缀中的相同前后缀最大长度（图中为2）肯定也与后缀中的相同前后缀最大长度（图中为2）相同，也说明了前缀中的前缀（图中为0和1上的A和B）等于后缀中的后缀（图中为10和11上的A和B），此时还是原来的思路temp为前缀中的前缀的下一位，判断是否与后缀中的后缀的下一位相同（就是当前的A[x]），如果相同就是第一种情况，next[x]
= temp + 1，如果一直没找到则设为0，说明没有。
学到这不得不感叹kmp三位大佬的恐怖。。 大体的思想就是这样，不过如果对于做题来说的话，有很多不一样的地方，比如王道书上的next数组是从下标1开始的，对于本文的内容，需要得到匹配失败位置-1的next数组值，因此书上将整体右移了一位，开头补上了-1，这样匹配失败的位置就是对应的next数组值。又下一次匹配要从最长前缀的下一位开始，而对于下标从0开始，next数组值就是下一位（前面解释了），而对于下标从1开始，需要再+1才是对应下标，因此也对next数组最后进行了+1操作。不管怎么样，next的含义都是最长前缀的下一个位置。主要思想都是一样的，随机应变即可。
代码：
class KMP:
def __init__(self, text, pattern) -> None:
self.text = text
self.pattern = pattern
self.next = []
def init_next(self):
self.next.append(0) # first
for i, s in enumerate(self.pattern[1:], 1):
tmp = self.next[i-1]
if s == self.pattern[tmp]:
self.next.append(tmp + 1)
else:
while self.pattern[tmp] != s and tmp != 0:
tmp = self.next[tmp-1]
if tmp == 0 and self.pattern[tmp] != s:
self.next.append(0)
continue
self.next.append(tmp + 1)
def search(self):
i = 0 # text index
j = 0 # partten index
while i < len(self.text):
if self.text[i] == self.pattern[j]:
i += 1
j += 1
elif j:
j = self.next[j-1]
else:
i += 1
if j == len(self.pattern):
return i - j
return -1
kmp = KMP("hello", "ll")
kmp.init_next()
print(kmp.search())
print(kmp.next)nextval
还有一种改进的next，因为匹配错误的位置重新移动指针后的位置的值可能与原来的值相同，因此在构建next数组的时候可以直接跳转到不相同的位置，这样就减小了重复的比较。 比如aaabaaaab和aaaab，当在主串中第一个b位置出错时，此时模式串为a，会比较str[next[2]]与b，但此时str[next[2]]也是a，再次比较也会错误，但再移动后发现还是a还是错误，这些比较都是没有意义的，最后要移动到模式串开头，然后将主串指针+1再比较，所以构建nextval减少了这些比较。 我是根据已经构建好的next数组推理来的。代码如下：
def create_nextval(self):
length = len(self.pattern)
self.nextval = [0] * length
for i in range(1, len(self.next)):
tmp = self.next[i-1]
if self.pattern[tmp] != self.pattern[i]:
self.nextval[i-1] = tmp
else:
while tmp and self.pattern[tmp] == self.pattern[i]:
tmp = self.next[tmp-1]
self.nextval[i-1] = tmp因为用不到最后一位的数值，所以考研书上就直接全部右移一位，理论上都是相同的。原理就是匹配错误的位置的字符和要跳转到的位置的字符相同的话就要继续跳转直到等于0或者不相同为止。