kd树
kd树
knn算法就是用kd树实现的
二分查找
很简单 就不说了
BST
很简单 就不说了
多维数组
假设数组B为\([[6, 2], [6, 3], [3, 5], [5, 0], [1, 2], [4, 9], [8, 1]]\),有一个元素x,我们要找到数组B中距离x最近的元素,应该如何实现呢?比较直接的想法是用数组B中的每一个元素与x求距离,距离最小的那个元素就是我们要找的元素。假设x = [1, 1],那么用数组B中的所有元素与x求距离得到[5.0, 5.4, 4.5, 4.1, 1.0, 8.5, 7.0],其中距离最小的是1,对应的元素是数组B中的[1, 2],所以[1, 2]就是我们的查找结果。
kd-tree
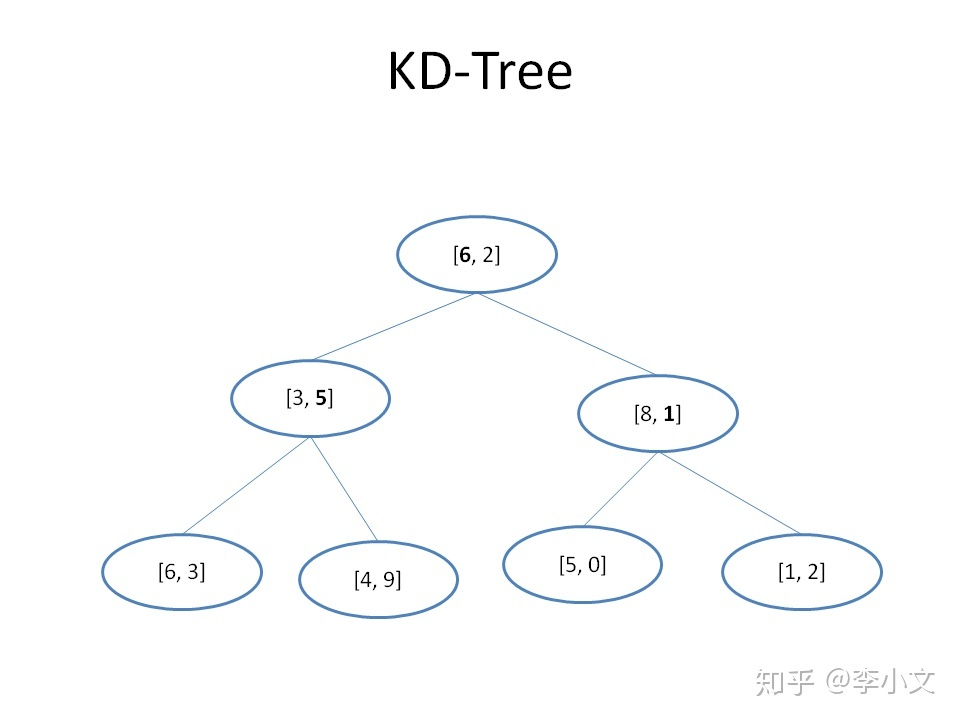
如何建立
你 1. 建立根节点;
选取方差最大的特征作为分割特征(或者根据深度选择)
选择该特征的中位数作为分割点;
将数据集中该特征小于中位数的传递给根节点的左儿子,大于中位数的传递给根节点的右儿子;
递归执行步骤2-4,直到所有数据都被建立到KD Tree的节点上为止。
不难看出,KD Tree的建立步骤跟BST是非常相似的,可以认为BST是KD Tree在一维数据上的特例。KD Tree的算法复杂度介于O(Log2(N))和O(N)之间。
为什么选择方差最大的维度
数据分割后分散的比较开,主要是为了减少回溯时间,减少子树的访问。
为什么选择中位数作为分割点
因为借鉴了BST,选取中位数,让左子树和右子树的数据数量一致,便于二分查找。
查找元素
- 从根节点出发进行查找,根据当前深度计算比较的特征维度,若目标节点的特征值小于当前节点的特征值则遍历左子树,否则遍历右子树
- 找到叶子结点后,将其暂时标记为当前最邻近的点
- 递归地向上回退,在回退时需要做:
- 如果当前节点与目标节点的距离更近,则更新最邻近节点为当前节点
- 如果当前节点对应特征与目标节点对应特征的值距离小于当前最小值时,进入当前节点的另一个子节点(因为刚刚从一个子节点遍历回来)进行查找(如果存在子节点的话),有可能存在更近的节点。否则的话继续向上回退。
- 回退到根节点结束。得到最邻近点。
class Node:
def __init__(self, data, left=None, right=None):
self.val = data
self.left = left
self.right = right
class KDTree:
def __init__(self, k):
self.k = k
def create_Tree(self, dataset, depth):
if not dataset:
return None
mid_index = len(dataset) // 2 # 中位数索引
axis = depth % self.k # 选择的维度
sort_dataset = sorted(dataset, key=(lambda x: x[axis])) # 按照维度排序
mid_data = sort_dataset[mid_index] # 中位数索引对应的数据
cur_node = Node(mid_data) # 创建节点
left_data = sort_dataset[:mid_index] # 左子树数据
right_data = sort_dataset[mid_index+1:] # 右子树数据
cur_node.left = self.create_Tree(left_data, depth+1) # 递归创建左子树
cur_node.right = self.create_Tree(right_data, depth+1) # 递归创建右子树
# print(cur_node.val)
return cur_node
def search(self, tree, new_data): # kd树的搜索
self.near_node = None # 最近的节点
self.near_val = None # 最近的节点的值
def dfs(node, depth):
if not node:
return
axis = depth % self.k # 当前深度对应选择的维度
if new_data[axis] < node.val[axis]: # 如果新数据的维度值小于当前节点的维度值
dfs(node.left, depth+1) # 递归搜索左子树
else:
dfs(node.right, depth+1) # 递归搜索右子树
# 到这就相当于到达了叶子节点
dist = self.distance(new_data, node.val) # 计算新数据与当前节点的距离
if not self.near_val or dist < self.near_val: # 如果当前节点的距离小于最近的节点的距离
self.near_val = dist # 更新最近的节点的距离
self.near_point = node.val # 更新最近的节点的值
#判断是否要进入兄弟节点寻找
if abs(new_data[axis] - node.val[axis]) < self.near_val: # 如果新数据的维度值与当前节点的维度值的差值小于最近的节点的距离,说明兄弟节点区域有可能存在更接近的值。
if new_data[axis] < node.val[axis]: # 控制去兄弟节点而不是刚刚回溯来的节点。
dfs(node.right, depth+1)
else:
dfs(node.left, depth+1)
dfs(tree, 0)
return self.near_point
def distance(self, point_1, point_2):
res = 0
for i in range(self.k):
res += (point_1[i] - point_2[i]) ** 2
return res ** 0.5
if __name__ == '__main__':
data_set = [[2,3],[5,4],[9,6],[4,7],[8,1],[7,2]]
new_data = [1,5]
k = len(data_set[0])
kd_tree = KDTree(k)
our_tree = kd_tree.create_Tree(data_set, 0)
predict = kd_tree.search(our_tree, new_data)
print('Nearest Point of {}: {}'.format(new_data,predict))Nearest Point of [1, 5]: [2, 3]借用一下别人画的解题过程
 ## 参考
## 参考