梯度提升决策树(GBDT)

GBDT(Gradient Boosting Decision Tree)是一种迭代的决策树算法，由多棵决策树组成，所有树的结论累加起来作为最终答案。

回归树

选择最优切分变量j与切分点s：遍历变量j，对规定的切分变量j扫描切分点s，选择使下式得到最小 值时的(j,s)对。其中Rm是被划分的输入空间， \(\mathrm{cm}\) 是空间Rm对应的固定输出值。

\[ \min_{j, s}\left[\min_{c_{1}} \sum_{x_{i} \in R_{i}(j, s)}\left(y_{i}-c_{1}\right)^{2}+\min_{c_{2}} \sum_{x_{i} \in R_{i}(j, s)}\left(y_{i}-c_{1}\right)^{2}\right] \]

用选定的(j,s)对，划分区域并决定相应的输出值

\[ \begin{gathered} R_{1}(j, s)=\{x \mid x^{(j)} \leq s\}, R_{2}(j, s)=\{x \mid x^{(j)}>s\} \\\\ \hat{c}_{m}=\frac{1}{N_{m}} \sum_{x_{i} \in R_{m}(j, s)} y_{i} \\\\ x \in R_{m}, m=1,2 \end{gathered} \]

继续对两个子区域调用上述步骤，将输入空间划分为 \(M\) 个区域R1,R2,..,Rm，生成决策树。

\[ f(x)=\sum_{m=1}^{M} \hat{c}_{m} I\left(x \epsilon R_{m}\right) \]

当输入空间划分确定时，可以用平方误差来表示回归树对于训练数据的预测方法，用平方误差最小 的准则求解每个单元上的最优输出值。

提升树

梯度提升树是提升树（Boosting Tree）的一种改进算法，所以在讲梯度提升树之前先来说一下提升树。

  先来个通俗理解：假如有个人30岁，我们首先用20岁去拟合，发现损失有10岁，这时我们用6岁去拟合剩下的损失，发现差距还有4岁，第三轮我们用3岁拟合剩下的差距，差距就只有一岁了。如果我们的迭代轮数还没有完，可以继续迭代下面，每一轮迭代，拟合的岁数误差都会减小。最后将每次拟合的岁数加起来便是模型输出的结果。

提升树算法: (1) 初始化 \(f_{0}(x)=0\) (2) 对 \(m=1,2, \ldots, M\) (a) 计算残差

\[ r_{m i}=y_{i}-f_{m-1}(x), i=1,2, \ldots, N \]

为什么残差是这种形式？ 当采用平方误差损失函数时,

\[ L(y, f(x))=(y-f(x))^2 \]

其损失变为

\[ \begin{aligned} L\left(y, f_{m-1}(x)+T\left(x ; \Theta_m\right)\right) &=\left[y-f_{m-1}(x)-T\left(x ; \Theta_m\right)\right]^2 \\\\ &=\left[r-T\left(x ; \Theta_m\right)\right]^2 \end{aligned} \]

这里,

\[ r=y-f_{m-1}(x) \]

也可以用上一步的残差（定义的上一步的标签）减去拟合上一步残差的回归树。即：

\[ r_{mi} = r_{(m-1)i} - h_{m-1}(x) \]

易证明这两种形式等价。 (b) 拟合残差 \(r_{m i}\) 学习一个回归树，得到 \(h_{m}(x)\) (c) 更新 \(f_{m}(x)=f_{m-1}+h_{m}(x)\) (3) 得到回归问题提升树

\[ f_{M}(x)=\sum_{m=1}^{M} h_{m}(x) \]

GBDT

GBDT与提升树不同的是GBDT使用负梯度来近似残差。

GBDT算法: (1) 初始化弱学习器

\[ f_{0}(x)=\arg \min_{c} \sum_{i=1}^{N} L\left(y_{i}, c\right) \]

2. 对 \(m=1,2, \ldots, M\) 有:

1. 对每个样本 \(i=1,2, \ldots, N\) ，计算负梯度，即残差

\[ r_{i m}=-\left[\frac{\left.\partial L\left(y_{i}, f\left(x_{i}\right)\right)\right)}{\partial f\left(x_{i}\right)}\right]_{f(x)=f_{m-1}(x)} \]

一般回归的损失函数就是均方误差，但缺点是对于outlier比较敏感。 因此可以选择使用MAE或者Huber loss。所以说负梯度并不等于残差，损失函数选择MSE的时候才可以划等号。

2. 将上步得到的残差作为样本新的真实值，并将数据 \(\left(x_{i}, r_{i m}\right), i=1,2, . . N\) 作为下棵树的训练数据，得到一颗新的回归树 \(f_{m}(x)\) 其对应的叶子节点区域为 \(R_{j m}, j=1,2, \ldots, J\) 。其中 \(J\) 为回归树的叶子节点的个数。
3. 对叶子区域 \(j=1,2, . . J\) 计算最佳拟合值

\[ \Upsilon_{j m}=\underbrace{\arg \min}_{\Upsilon} \sum_{x_{i} \in R_{j m}} L\left(y_{i}, f_{m-1}\left(x_{i}\right)+\Upsilon\right) \]

也可以理解为：

\[ \Upsilon_{jm} = \underbrace{\arg \min}_{\Upsilon} \sum_{x_i \in R_{jm}} L(r_{im}, \Upsilon) \]

损失函数L为MSE时，就与回归树的构建类似，最佳拟合值就是划分的叶子节点的均值。可以简单理解为提升树和GBDT的区别就是计算残差的方式不同。

4. 更新强学习器

\[ f_{m}(x)=f_{m-1}(x)+\sum_{j=1}^{J} \Upsilon_{j m} I\left(x \in R_{j m}\right) \]

3. 得到最终学习器

\[ f(x)=f_{M}(x)=f_{0}(x)+\sum_{m=1}^{M} \sum_{j=1}^{J} \Upsilon_{j m} I\left(x \in R_{j m}\right) \]

实例可以看参考里面。

与梯度下降算法的关系

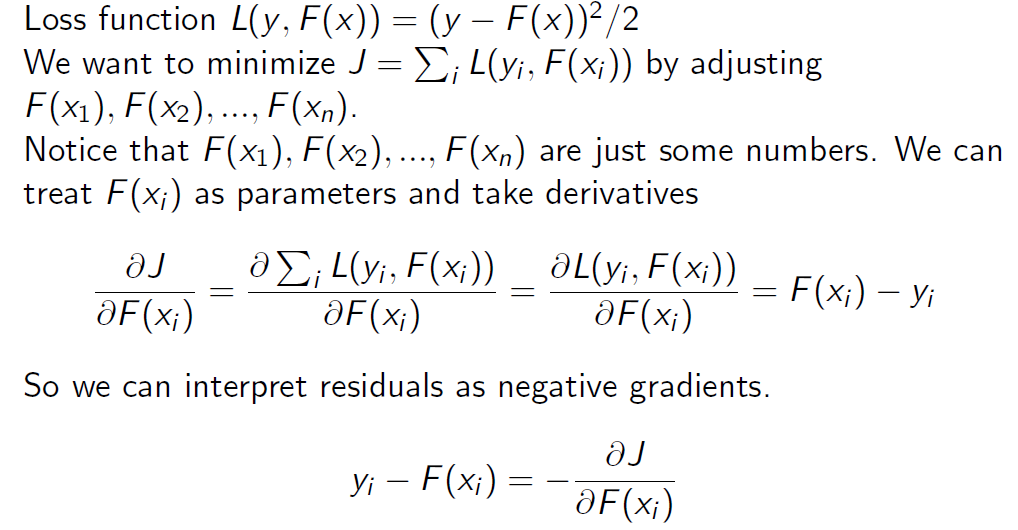
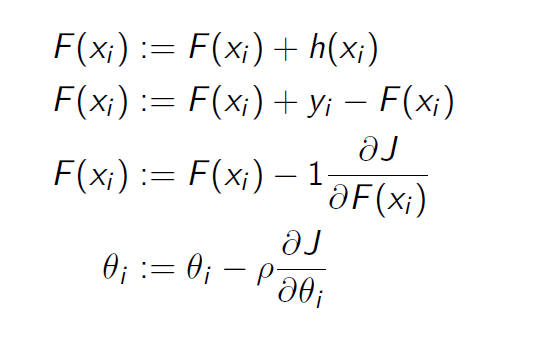
代码

import numpy as np

class RegressionTree:

    def __init__(self, max_depth=2, min_samples_split=2):

        self.max_depth = max_depth

        self.min_samples_split = min_samples_split

        self.tree = {}

    def fit(self, X, y):

        self.X = X

        self.y = y

        self.n_features = X.shape[1]

        self.n_samples = X.shape[0]

        self.tree = self._build_tree(X, y)

    def predict(self, X):

        return np.array([self._predict(inputs) for inputs in X])

    def _build_tree(self, X, y, depth=0):

        m = X.shape[0]

        n = X.shape[1]

        # 1. 终止条件

        if m <= self.min_samples_split or depth >= self.max_depth:

            return self._leaf(y)

        # 2. 找到最优分裂特征和特征值

        feature, value = self._best_split(X, y)

        # 3. 构建子树

        left_idx, right_idx = self._split(X, feature, value)

        left = self._build_tree(X[left_idx, :], y[left_idx], depth + 1)

        right = self._build_tree(X[right_idx, :], y[right_idx], depth + 1)

        return {"feature": feature, "value": value, "left": left, "right": right}

    def _leaf(self, y):

        return np.mean(y)

    def _best_split(self, X, y):

        m = X.shape[0]

        n = X.shape[1]

        min_mse = np.inf

        best_feature = None

        best_value = None

        for feature in range(n):

            values = np.unique(X[:, feature])

            for value in values:

                y1 = y[X[:, feature] < value]

                y2 = y[X[:, feature] >= value]

                mse = np.mean(y1) - np.mean(y2)

                if mse < min_mse:

                    min_mse = mse

                    best_feature = feature

                    best_value = value

        return best_feature, best_value

    def _split(self, X, feature, value):

        left_idx = np.argwhere(X[:, feature] < value).flatten()

        right_idx = np.argwhere(X[:, feature] >= value).flatten()

        return left_idx, right_idx

  

class GBDT:

    def __init__(self, n_estimators=10, learning_rate=0.1, max_depth=3):

        self.n_estimators = n_estimators

        self.learning_rate = learning_rate

        self.max_depth = max_depth

        self.trees = []

    def fit(self, X, y):

        y_pred = np.zeros_like(y, dtype=np.float)

        for i in range(self.n_estimators):

            tree = RegressionTree(self.max_depth)

            tree.fit(X, -self.gradient(y, y_pred))

            y_pred += self.learning_rate * tree.predict(X)

            self.trees.append(tree)

    def predict(self, X):

        y_pred = np.zeros((X.shape[0], ), dtype=np.float)

        for tree in self.trees:

            y_pred += self.learning_rate * tree.predict(X)

        return y_pred

    def gradient(self, y_true, y_pred):

        return y_true - y_pred

为什么xgboost/gbdt在调参时为什么树的深度很少就能达到很高的精度？

Boosting主要关注降低偏差，因此Boosting能基于泛化性能相当弱的学习器构建出很强的集成；Bagging主要关注降低方差，因此它在不剪枝的决策树、神经网络等学习器上效用更为明显。

对于Bagging算法来说，由于我们会并行地训练很多不同的分类器的目的就是降低这个方差(variance) ,因为采用了相互独立的基分类器多了以后，h的值自然就会靠近。所以对于每个基分类器来说，目标就是如何降低这个偏差（bias),所以我们会采用深度很深甚至不剪枝的决策树。

对于Boosting来说，每一步我们都会在上一轮的基础上更加拟合原数据，所以可以保证偏差（bias）,所以对于每个基分类器来说，问题就在于如何选择variance更小的分类器，即更简单的分类器，所以我们选择了深度很浅的决策树。 ## 参考

https://blog.csdn.net/zpalyq110/article/details/79527653 https://zhuanlan.zhihu.com/p/280222403