GAN

简介

生成对抗网络（Generative Adversarial Network，简称GAN）是无监督学习的一种方法，通过让两个神经网络相互博弈的方式进行学习。

大白话： 说就是生成对抗网络有一个生成网络和一个判别网络，假设有一个真实数据和一个生成网络生成的假数据，那么判别网络就是识别出这两种数据，判别网络努力分类成功，生成网络努力生成和真实数据相似的数据使判别网络分类不出来。这就是所说的相互博弈的方式。

专业的话： 生成式对抗网络由生成器和判别器构成。生成对抗网络的核心目的是训练生成器。生成器的目的是生成与真实样本尽可能相似的“假样本”，判别器的目的是尽可能区分出给定样本是真实样本还是生成的“假样本”。二者目的相悖，在不断博弈的过程中相互提高，最终在判别器判别能力足够可靠的前提下仍无法区分给定样本是真实样本还是生成样本，从而我们说生成器能够生成“以假乱真”的样本。

优化

优化目标 - 价值函数 (Value Function) \(\min_G \max_D V(D, G)=\mathbb{E}_{\boldsymbol{x} \sim p_{\text {data }}(\boldsymbol{x})}[\log D(\boldsymbol{x})]+\mathbb{E}_{\boldsymbol{z} \sim p_{\boldsymbol{z}}(\boldsymbol{z})}[\log (1-D(G(\boldsymbol{z})))]\) - 优化方式 - 生成器优化方向: 最小化价值函数 - 判别器优化方向: 最大化价值函数

简单理解，判别器就是要使正确的样本分为1，生成的样本分为0，那么就是最大化价值函数。 生成器就是要以假乱真，使判别器判生成的样本为1，即最大化\(D(G(z))\)，就是最小化价值函数。

这里的价值函数与交叉熵类似。真实样本为正例，生成样本为负例，一般都是最小化损失函数，因此需要做一下变形：

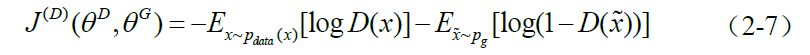
这个很好理解，与交叉熵一样。

上面是判别器的优化，下面是生成器的优化：

总的来说，生成器得损失函数就是

\[ J^{(G)} = -\frac{1}{2}E_z\log D(G(z)) \] 即“以假乱真”。