flash attention
Safe softmax 并没有 1-pass 算法,那么 Attention 会不会有呢?有!这就是 FlashAttention!
在使用 online attention 的情况下,从头开始计算 attention score 的过程如下: \(\operatorname{NOTATIONS}\)
\(Q[k,:]:\) the \(k\) -th row vector of \(Q\) matrix. \(\begin{aligned}O[k,:]:\mathrm{~the~}k\text{-th row of output }O\mathrm{~matrix.}\\\mathbf{V}[i,i]:\mathrm{~the~}k\text{-th row of output }O\mathrm{~matrix.}\end{aligned}\) \(V[i,:]{:\text{ the }i\text{-th row of }V\text{ matrix}}.\) \(\{\boldsymbol{o}_i\}{:}\sum_{j=1}^ia_jV[j,:]\), a row vector storing partial aggregation result \(A[k,:i]\times V[:i,:]\) BODY
\(\textbf{for }i\leftarrow 1, N\textbf{ do}\) \[\begin{aligned}x_i&\leftarrow\quad Q[k,:]\:K^T[:,i]\\m_i&\leftarrow\quad\max\left(m_{i-1},x_i\right)\\d_i'&\leftarrow\quad d_{i-1}'e^{m_{i-1}-m_i}+e^{x_i-m_i}\end{aligned}\] \(\mathbf{end}\)
\(\textbf{for }i\leftarrow 1, N\textbf{ do}\) \[\begin{aligned}&a_i\:\leftarrow\:\frac{e^{x_i-m_N}}{d_N^{\prime}}\\&o_i\:\leftarrow\:o_{i-1}+a_i\:V[i,:\:]\end{aligned}\] \(\mathbf{end}\) \[O[k,:]\leftarrow\boldsymbol{o}_N\]
优化思路和 online attention 一样,将 \(o_{i}\) 的计算简化以便于可以写成迭代式。
原来的 \(o_{i}\) 使用以下方式计算,依赖于全局的 \(m_{N}\) 和 \(d_{N}\)。 \[\boldsymbol{o}_i:=\sum_{j=1}^i\left(\frac{e^{x_j-m_N}}{d_N^{\prime}}V[j,:]\right)\] 将其改写成如下形式: \[\boldsymbol{o}_i^{\prime}:=\left(\sum_{j=1}^i\frac{e^{x_j-m_i}}{d_i^{\prime}}V[j,:]\right)\] 这样按照上面的方式拓展下去,可以找到一个循环迭代式。
\[\begin{aligned} \mathbf{o}_i^{\prime}& =\sum_{j=1}^i\frac{e^{x_j-m_i}}{d'}V[j,:] \\ &= \left(\sum_{j=1}^{i-1}\frac{e^{x_j-m_i}}{d_i^{\prime}}V[j,:] \right)+\frac{e^{x_i-m_i}}{d_i^{\prime}}V[i,:] \\ &= \left(\sum_{j=1}^{i-1}\frac{e^{x_j-m_{i-1}}}{d_{i-1}^{\prime}}\frac{e^{x_j-m_i}}{e^{x_j-m_{i-1}}}\frac{d_{i-1}^{\prime}}{d_i^{\prime}}V[j,:]\right)+\frac{e^{x_i-m_i}}{d_i^{\prime}}V[i,:] \\ &= \left(\sum_{j=1}^{i-1}\frac{e^{x_j-m_{i-1}}}{d_{i-1}^{\prime}}V[j,.]\right)\frac{d_{i-1}^{\prime}}{d_i^{\prime}}e^{m_{i-1}-m_i}+\frac{e^{x_i-m_i}}{d_i^{\prime}}V[i,.] \\ &= \boldsymbol{o}_{i-1}'\frac{d_{i-1}'e^{m_{i-1}-m_i}}{d_i'}+\frac{e^{x_i-m_i}}{d_i'}V[i,:] \end{aligned}\]
这样就找到了 \(o_{i}\) 的递推表达式。
之后对 Q, K 进行 tiling 后计算,得到如下: \[\begin{aligned}&\textbf{for
}i\leftarrow1,\#\text{tiles
do}\\&&&\boldsymbol{x}_i\quad\leftarrow\quad Q[k;\cdot]
K^T[\cdot,(i-1) b; i
b]\\&&&m_i^{(\mathrm{local})}=\begin{array}{c}\overset{b}{\operatorname*{max}}\left(\boldsymbol{x}_i[j]\right)\\\end{array}\\&&&m_i
\leftarrow
\max\left(m_{i-1},m_i^{(\mathrm{local})}\right)\\&&&a_i^{\prime}
\leftarrow
d_{i-1}^{\prime}e^{m_{i-1}-m_i}+\sum_{j=1}^be^{\boldsymbol{x}_i[j]-m_i}\\&&&\boldsymbol{o}_i^{\prime}
\leftarrow
\boldsymbol{o}_{i-1}^{\prime}\frac{d_{i-1}^{\prime}e^{m_{i-1}-m_i}}{d_i^{\prime}}+\sum_{j=1}^b\frac{e^{\boldsymbol{x}_i[j]-m_i}}{d_i^{\prime}}V[(i-1)
b+j,:]\\&\text{end}\\&&&O[k,:]\leftarrow\boldsymbol{o}_{N/b}^{\prime}\end{aligned}\]
对于 tiles,示意图如下: 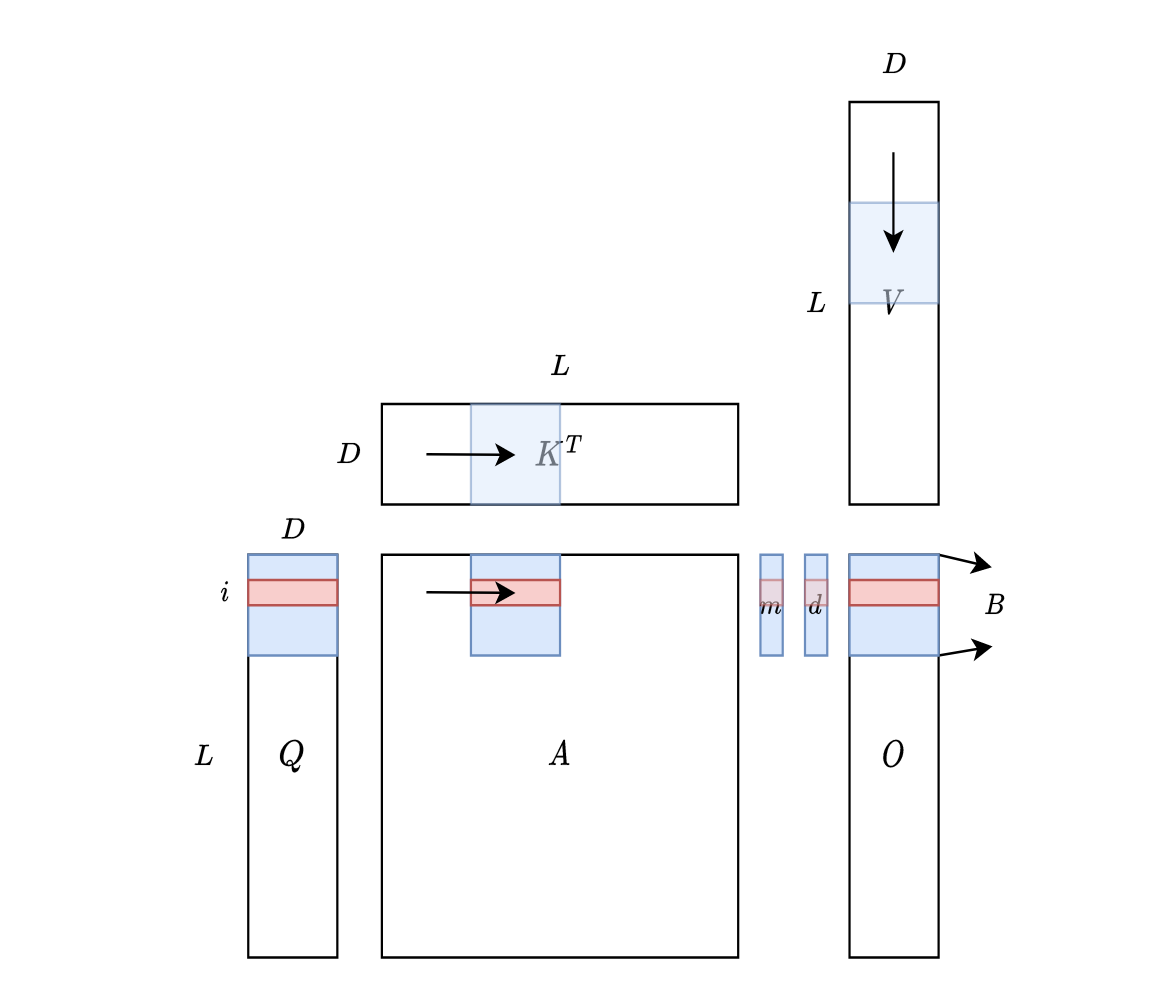
可以理解成滑动窗口,\(K^{T}\) 从左向右滑动(按列读取),\(V\) 从上向下滑动(按行读取)。也可以直接理解成分块矩阵,具体为什么这么做,参考:Cuda 编程之 Tiling - 知乎 (zhihu.com)