EM算法

引入

我们经常会从样本观察数据中，找出样本的模型参数。 最常用的方法就是极大化模型分布的对数似然函数。（最大似然估计：利用已知的样本结果，反推最有可能导致这样结果的一组参数）但是在一些情况下，我们得到的观察数据有未观察到的隐含数据，此时我们未知的有隐含数据和模型参数，因而无法直接用极大化对数似然函数得到模型分布的参数。用EM算法可以解决。

EM算法是一种迭代算法，用于含有隐变量的概率模型参数的极大似然估计，或极大后验概率估计。

EM算法的每次迭代由两步组成：E步，求期望；M步，求极大。所以被称为期望极大算法。

EM算法解决这个的思路是使用启发式的迭代方法，既然我们无法直接求出模型分布参数，那么我们可以先猜想隐含数据（EM算法的E步），接着基于观察数据和猜测的隐含数据一起来极大化对数似然，求解我们的模型参数（EM算法的M步)。由于我们之前的隐藏数据是猜测的，所以此时得到的模型参数一般还不是我们想要的结果。不过没关系，我们基于当前得到的模型参数，继续猜测隐含数据（EM算法的E步），然后继续极大化对数似然，求解我们的模型参数（EM算法的M步)。以此类推，不断的迭代下去，直到模型分布参数基本无变化，算法收敛，找到合适的模型参数。

三硬币模型

首先介绍一个使用 EM算法的例子。 (三硬币模型) 假设有 3 枚硬币, 分别记作 A, B, C。这些硬币正面出现 的概率分别是 \(\pi, p\) 和 \(q\) 。进行如下郑硬币试验: 先掷硬币 \(\mathrm{A}\), 根据其结果选出硬币 \(\mathrm{B}\) 或硬币 \(\mathrm{C}\), 正面选硬币 \(\mathrm{B}\), 反面选硬币 \(\mathrm{C}\); 然后郑选出的硬币, 掷硬币的结果, 出现正 面记作 1 , 出现反面记作 0 ; 独立地重复 \(n\) 次试验 (这里, \(n=10\) ), 观测结果如下:

\[ 1,1,0,1,0,0,1,0,1,1 \]

假设只能观测到郑硬币的结果, 不能观测郑硬币的过程。问如何估计三硬币正面出现 的概率, 即三硬币模型的参数。

解 三硬币模型可以写作

\[ \begin{aligned} P(y \mid \theta) &=\sum_z P(y, z \mid \theta)=\sum_z P(z \mid \theta) P(y \mid z, \theta) \\\\ &=\pi p^y(1-p)^{1-y}+(1-\pi) q^y(1-q)^{1-y} \end{aligned} \]

这里, 随机变量 \(y\) 是观测变量, 表示一次试验观测的结果是 1 或 0 ; 随机变量 \(z\) 是隐 变量, 表示末观测到的掷硬币 \(\mathrm{A}\) 的结果; \(\theta=(\pi, p, q)\) 是模型参数。这一模型是以上数 据的生成模型。注意, 随机变量 \(y\) 的数据可以观测, 随机变量 \(z\) 的数据不可观测。 将观测数据表示为 \(Y=\left(Y_1, Y_2, \cdots, Y_n\right)^{\mathrm{T}}\), 末观测数据表示为 \(Z=\left(Z_1, Z_2, \cdots, Z_n\right)^{\mathrm{T}}\) 则观测数据的似然函数为

\[ P(Y \mid \theta)=\sum_Z P(Z \mid \theta) P(Y \mid Z, \theta) \]

即

\[ P(Y \mid \theta)=\prod_{j=1}^n\left[\pi p^{y_j}(1-p)^{1-y_j}+(1-\pi) q^{y_j}(1-q)^{1-y_j}\right] \]

考虑求模型参数 \(\theta=(\pi, p, q)\) 的极大似然估计, 即

\[ \hat{\theta}=\arg \max_\theta \log P(Y \mid \theta) \]

这个问题没有解析解, 只有通过迭代的方法求解。EM算法就是可以用于求解这 个问题的一种迭代算法。下面给出针对以上问题的 EM算法, 其推导过程省略。

EM算法首先选取参数的初值, 记作 \(\theta^{(0)}=\left(\pi^{(0)}, p^{(0)}, q^{(0)}\right)\), 然后通过下面的 步骤迭代计算参数的估计值, 直至收敛为止。第 \(i\) 次迭代参数的估计值为 \(\theta^{(i)}=\) \(\left(\pi^{(i)}, p^{(i)}, q^{(i)}\right)\) 。EM算法的第 \(i+1\) 次迭代如下。 \(\mathrm{E}\) 步：计算在模型参数 \(\pi^{(i)}, p^{(i)}, q^{(i)}\) 下观测数据 \(y_j\) 来自郑硬币 \(\mathrm{B}\) 的概率。这里就是使用的贝叶斯定理。

\[ \mu_j^{(i+1)}=\frac{\pi^{(i)}\left(p^{(i)}\right)^{y_j}\left(1-p^{(i)}\right)^{1-y_j}}{\pi^{(i)}\left(p^{(i)}\right)^{y_j}\left(1-p^{(i)}\right)^{1-y_j}+\left(1-\pi^{(i)}\right)\left(q^{(i)}\right)^{y_j}\left(1-q^{(i)}\right)^{1-y_j}} \]

\(\mathrm{M}\) 步：计算模型参数的新估计值

\[ \pi^{(i+1)}=\frac{1}{n} \sum_{j=1}^n \mu_j^{(i+1)} \]

\[ \begin{gathered} p^{(i+1)}=\frac{\sum_{j=1}^n \mu_j^{(i+1)} y_j}{\sum_{j=1}^n \mu_j^{(i+1)}} \\\\ q^{(i+1)}=\frac{\sum_{j=1}^n\left(1-\mu_j^{(i+1)}\right) y_j}{\sum_{j=1}^n\left(1-\mu_j^{(i+1)}\right)} \end{gathered} \]

进行数值计算。假设模型参数的初值取为

\[ \pi^{(0)}=0.5, \quad p^{(0)}=0.5, \quad q^{(0)}=0.5 \]

对 \(y_j=1\) 与 \(y_j=0\) 均有 \(\mu_j^{(1)}=0.5\) 。 利用迭代公式, 得到

\[ \pi^{(1)}=0.5, \quad p^{(1)}=0.6, \quad q^{(1)}=0.6 \]

\[ \mu_j^{(2)}=0.5, \quad j=1,2, \cdots, 10 \]

继续迭代, 得

\[ \pi^{(2)}=0.5, \quad p^{(2)}=0.6, \quad q^{(2)}=0.6 \]

于是得到模型参数 \(\theta\) 的极大似然估计:

\[ \hat{\pi}=0.5, \quad \hat{p}=0.6, \quad \hat{q}=0.6 \]

\(\pi=0.5\) 表示硬币 A 是均匀的, 这一结果容易理解。

如果取初值 \(\pi^{(0)}=0.4, p^{(0)}=0.6, q^{(0)}=0.7\), 那么得到的模型参数的极大似然 估计是 \(\hat{\pi}=0.4064, \hat{p}=0.5368, \hat{q}=0.6432\) 。这就是说, EM算法与初值的选择有关, 选择不同的初值可能得到不同的参数估计值。

一般地, 用 \(Y\) 表示观测随机变量的数据, \(Z\) 表示隐随机变量的数据。 \(Y\) 和 \(Z\) 连 在一起称为完全数据 (complete-data), 观测数据 \(Y\) 又称为不完全数据 (incompletedata）。假设给定观测数据 \(Y\), 其概率分布是 \(P(Y \mid \theta)\), 其中 \(\theta\) 是需要估计的模型参数, 那么不完全数据 \(Y\) 的似然函数是 \(P(Y \mid \theta)\), 对数似然函数 \(L(\theta)=\log P(Y \mid \theta)\); 假设 \(Y\) 和 \(Z\) 的联合概率分布是 \(P(Y, Z \mid \theta)\), 那么完全数据的对数似然函数是 \(\log P(Y, Z \mid \theta)\) 。

算法步骤

输入: 观测变量数据 \(Y\), 隐变量数据 \(Z\), 联合分布 \(P(Y, Z \mid \theta)\), 条件分布 \(P(Z \mid Y, \theta)\); 输出：模型参数 \(\theta\) 。 （1）选择参数的初值 \(\theta^{(0)}\), 开始迭代; (2) \(\mathrm{E}\) 步: 记 \(\theta^{(i)}\) 为第 \(i\) 次迭代参数 \(\theta\) 的估计值, 在第 \(i+1\) 次迭代的 \(\mathrm{E}\) 步, 计算

\[ \begin{aligned} Q\left(\theta, \theta^{(i)}\right) &=E_Z\left[\log P(Y, Z \mid \theta) \mid Y, \theta^{(i)}\right] \\\\ &=\sum_Z \log P(Y, Z \mid \theta) P\left(Z \mid Y, \theta^{(i)}\right) \end{aligned} \]

这里, \(P\left(Z \mid Y, \theta^{(i)}\right)\) 是在给定观测数据 \(Y\) 和当前的参数估计 \(\theta^{(i)}\) 下隐变量数据 \(Z\) 的条 件概率分布; (3) \(\mathrm{M}\) 步：求使 \(Q\left(\theta, \theta^{(i)}\right)\) 极大化的 \(\theta\), 确定第 \(i+1\) 次迭代的参数的估计值 \(\theta^{(i+1)}\)

\[ \theta^{(i+1)}=\arg \max_\theta Q\left(\theta, \theta^{(i)}\right) \]

4. 重复第 (2) 步和第 (3) 步, 直到收敛。

Q函数

函数 \(Q\left(\theta, \theta^{(i)}\right)\) 是 EM算法的核心, 称为 \(Q\) 函数 ( \(Q\) function)。 \({Q}\) 函数 : 完全数据 的对数似然函数 \(\log P(Y, Z \mid \theta)\) 关于在给定观测数 据 \(Y\) 和当前参数 \(\theta^{(i)}\) 下对未观测数据 \(Z\) 的条件概率分布 \(P\left(Z \mid Y, \theta^{(i)}\right)\) 的期望称为 \(Q\) 函数, 即

\[ Q\left(\theta, \theta^{(i)}\right)=E_Z\left[\log P(Y, Z \mid \theta) \mid Y, \theta^{(i)}\right] = \sum_Z \log P(Y,Z\mid \theta) P\left (Z\mid Y, \theta^{(i)}\right) \]

Jensen不等式

如果f是凸函数，X是随机变量，那么有

\[ E[f(X)] \geq f[E(X)] \]

如果f是凹函数则相反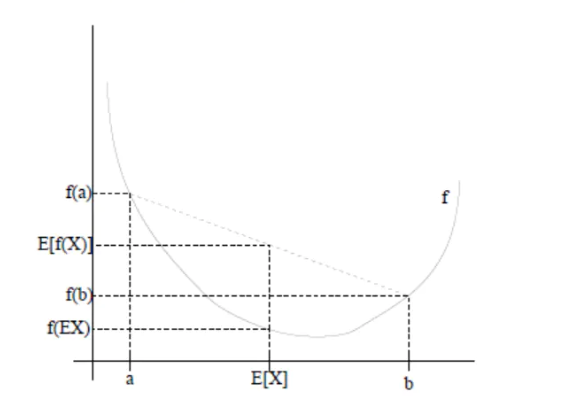

这个图可以比较清晰的看出这个结论。

EM算法的导出

为什么 EM算法能近似实现对观测数据的极大似然估计 呢? 下面通过近似求解观测数据的对数似然函数的极大化问题来导出 EM算法, 由此 可以清楚地看出 EM算法的作用。

我们面对一个含有隐变量的概率模型, 目标是极大化观测数据 (不完全数据) \(Y\) 关于参数 \(\theta\) 的对数似然函数, 即极大化

\[ \begin{aligned} L(\theta) &=\log P(Y \mid \theta)=\log \sum_Z P(Y, Z \mid \theta) \\\\ &=\log \left(\sum_Z P(Y \mid Z, \theta) P(Z \mid \theta)\right) \end{aligned} \]

注意到这一极大化的主要困难是式中有末观测数据并有包含和 (或积分) 的 对数。 事实上, EM算法是通过迭代逐步近似极大化 \(L(\theta)\) 的。假设在第 \(i\) 次迭代后 \(\theta\) 的 估计值是 \(\theta^{(i)}\) 。我们希望新估计值 \(\theta\) 能使 \(L(\theta)\) 增加, 即 \(L(\theta)>L\left(\theta^{(i)}\right)\), 并逐步达到极 大值。为此, 考虑两者的差:

\[ L(\theta)-L\left(\theta^{(i)}\right)=\log \left(\sum_Z P(Y \mid Z, \theta) P(Z \mid \theta)\right)-\log P\left(Y \mid \theta^{(i)}\right) \]

利用 Jensen 不等式 (Jensen inequality)得到其下界，这里的f即为log函数，是凹函数，则结论与凸函数时的结论是相反的。:

\[ \begin{aligned} L(\theta)-L\left(\theta^{(i)}\right) &=\log \left(\sum_Z P\left(Z \mid Y, \theta^{(i)}\right) \frac{P(Y \mid Z, \theta) P(Z \mid \theta)}{P\left(Z \mid Y, \theta^{(i)}\right)}\right)-\log P\left(Y \mid \theta^{(i)}\right) \\\\ & \geqslant \sum_Z P\left(Z \mid Y, \theta^{(i)}\right) \log \frac{P(Y \mid Z, \theta) P(Z \mid \theta)}{P\left(Z \mid Y, \theta^{(i)}\right)}-\log P\left(Y \mid \theta^{(i)}\right) \\\\ &=\sum_Z P\left(Z \mid Y, \theta^{(i)}\right) \log \frac{P(Y \mid Z, \theta) P(Z \mid \theta)}{P\left(Z \mid Y, \theta^{(i)}\right) P\left(Y \mid \theta^{(i)}\right)} \end{aligned} \]

令

\[ B\left(\theta, \theta^{(i)}\right) \hat{=} L\left(\theta^{(i)}\right)+\sum_Z P\left(Z \mid Y, \theta^{(i)}\right) \log \frac{P(Y \mid Z, \theta) P(Z \mid \theta)}{P\left(Z \mid Y, \theta^{(i)}\right) P\left(Y \mid \theta^{(i)}\right)} \]

则要求：

\[ L(\theta) \geqslant B\left(\theta, \theta^{(i)}\right) \]

即函数 \(B\left(\theta, \theta^{(i)}\right)\) 是 \(L(\theta)\) 的一个下界, 可知,

\[ L\left(\theta^{(i)}\right)=B\left(\theta^{(i)}, \theta^{(i)}\right) \]

因此, 任何可以使 \(B\left(\theta, \theta^{(i)}\right)\) 增大的 \(\theta\), 也可以使 \(L(\theta)\) 增大。这里回顾一下我们最原始的目标，就是为了最大化\(L(\theta)\)，为了使 \(L(\theta)\) 有尽可能大 的增长, 选择 \(\theta^{(i+1)}\) 使 \(B\left(\theta, \theta^{(i)}\right)\) 达到极大, 即

\[ \theta^{(i+1)}=\arg \max_\theta B\left(\theta, \theta^{(i)}\right) \]

现在求 \(\theta^{(i+1)}\) 的表达式。省去对 \(\theta\) 的极大化而言是常数的项

\[ \begin{aligned} \theta^{(i+1)} &=\arg \max_\theta\left(L\left(\theta^{(i)}\right)+\sum_Z P\left(Z \mid Y, \theta^{(i)}\right) \log \frac{P(Y \mid Z, \theta) P(Z \mid \theta)}{P\left(Z \mid Y, \theta^{(i)}\right) P\left(Y \mid \theta^{(i)}\right)}\right) \\\\ &=\arg \max_\theta\left(\sum_Z P\left(Z \mid Y, \theta^{(i)}\right) \log (P(Y \mid Z, \theta) P(Z \mid \theta))\right) \\\\ &=\arg \max_\theta\left(\sum_Z P\left(Z \mid Y, \theta^{(i)}\right) \log P(Y, Z \mid \theta)\right) \\\\ &=\arg \max_\theta Q\left(\theta, \theta^{(i)}\right) \end{aligned} \]

这等价于 EM算法的一次迭代, 即求 \(Q\) 函数及其极大化。EM算法是通过 不断求解下界的极大化逼近求解对数似然函数极大化的算法。 下图给出 EM算法的直观解释。注意两个曲线的交点就是在\(\theta^{(i)}\)

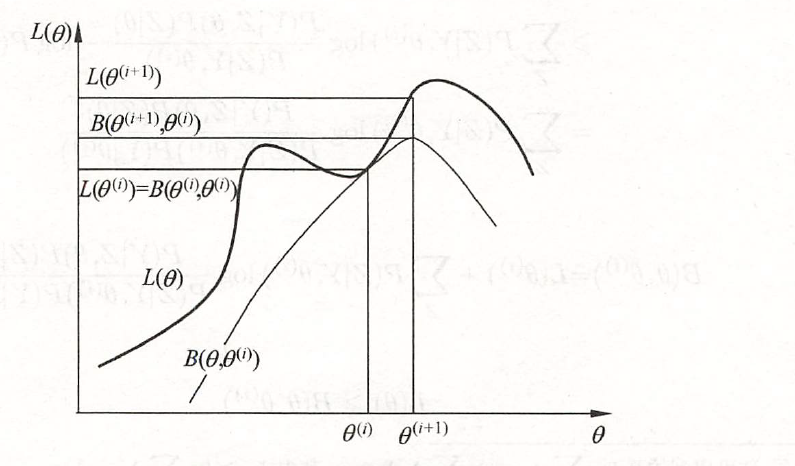这里其实就是相当于推导为什么最大化Q函数对应的参数就是当前迭代的最佳参数。

高斯混合模型

高斯混合模型是指有如下形式的概率分布模型：

\[ P(y\mid \theta ) = \sum_{k=1}^K\alpha_k \Phi(y\mid \theta_k) \]

其中\(\alpha_k\)为系数，\(\alpha_k \geq 0, \sum_{k=1}^K\alpha_k=1\); \(\Phi(y\mid \theta_k)\)为高斯密度函数，\(\theta_k=(\mu_k,\sigma_k^2)\)

\[ \Phi(y\mid \theta_k) = \frac{1}{\sqrt{2\pi}\sigma_k}\exp \left(-\frac{(y-\mu_k)^2}{2\sigma_k^2} \right) \]

为第k个模型。

EM算法的应用

1. 明确隐变量, 写出完全数据的对数似然函数 可以设想观测数据 \(y_j, j=1,2, \cdots, N\), 是这样产生的: 首先依概率 \(\alpha_k\) 选择第 \(k\) 个高斯分布分模型 \(\phi\left(y \mid \theta_k\right)\), 然后依第 \(k\) 个分模型的概率分布 \(\phi\left(y \mid \theta_k\right)\) 生成观测数据 \(y_j\) 。这时观测数据 \(y_j, j=1,2, \cdots, N\), 是已知的; 反映观测数据 \(y_j\) 来自第 \(k\) 个分模 型的数据是末知的, \(k=1,2, \cdots, K\), 以隐变量 \(\gamma_{j k}\) 表示, 其定义如下:

\[ \gamma_{j k}= \begin{cases}1, & \text { 第 } j \text { 个观测来自第 } k \text { 个分模型 } \\\\ 0, & \text { 否则 }\end{cases} \]

\[ j=1,2, \cdots, N ; \quad k=1,2, \cdots, K \]

\(\gamma_{j k}\) 是 0-1 随机变量。 有了观测数据 \(y_j\) 及末观测数据 \(\gamma_{j k}\), 那么完全数据是

\[ \left(y_j, \gamma_{j 1}, \gamma_{j 2}, \cdots, \gamma_{j K}\right), \quad j=1,2, \cdots, N \]

于是, 可以写出完全数据的似然函数:

\[ \begin{aligned} P(y, \gamma \mid \theta) &=\prod_{j=1}^N P\left(y_j, \gamma_{j 1}, \gamma_{j 2}, \cdots, \gamma_{j K} \mid \theta\right) \\\\ &=\prod_{k=1}^K \prod_{j=1}^N\left[\alpha_k \phi\left(y_j \mid \theta_k\right)\right]^{\gamma_{j k}} \\\\ &=\prod_{k=1}^K \alpha_k^{n_k} \prod_{j=1}^N\left[\phi\left(y_j \mid \theta_k\right)\right]^{\gamma_{j k}} \\\\ &=\prod_{k=1}^K \alpha_k^{n_k} \prod_{j=1}^N\left[\frac{1}{\sqrt{2 \pi} \sigma_k} \exp \left(-\frac{\left(y_j-\mu_k\right)^2}{2 \sigma_k^2}\right)\right]^{\gamma_{j k}} \end{aligned} \]

式中, \(n_k=\sum_{j=1}^N \gamma_{j k}, \sum_{k=1}^K n_k=N\) 。 那么, 完全数据的对数似然函数为

\[ \log P(y, \gamma \mid \theta)=\sum_{k=1}^K\left\\{n_k \log \alpha_k+\sum_{j=1}^N \gamma_{j k}\left[\log \left(\frac{1}{\sqrt{2 \pi}}\right)-\log \sigma_k-\frac{1}{2 \sigma_k^2}\left(y_j-\mu_k\right)^2\right]\right\} \]

2. EM 算法的 \(\mathrm{E}\) 步: 确定 \(Q\) 函数

\[ \begin{aligned} Q\left(\theta, \theta^{(i)}\right) &=E\left[\log P(y, \gamma \mid \theta) \mid y, \theta^{(i)}\right] \\\\ &=E\left{\sum_{k=1}^K\left{n_k \log \alpha_k+\sum_{j=1}^N \gamma_{j k}\left[\log \left(\frac{1}{\sqrt{2 \pi}}\right)-\log \sigma_k-\frac{1}{2 \sigma_k^2}\left(y_j-\mu_k\right)^2\right]\right}\right} \\\\ &=\sum_{k=1}^K\left\\{\sum_{j=1}^N\left(E \gamma_{j k}\right) \log \alpha_k+\sum_{j=1}^N\left(E \gamma_{j k}\right)\left[\log \left(\frac{1}{\sqrt{2 \pi}}\right)-\log \sigma_k-\frac{1}{2 \sigma_k^2}\left(y_j-\mu_k\right)^2\right]\right} \end{aligned} \]

这里需要计算 \(E\left(\gamma_{j k} \mid y, \theta\right)\), 记为 \(\hat{\gamma}_{j k}\) 。

\[ \begin{aligned} \hat{\gamma}_{j k} &=E\left(\gamma_{j k} \mid y, \theta\right)=P\left(\gamma_{j k}=1 \mid y, \theta\right) \\\\ &=\frac{P\left(\gamma_{j k}=1, y_j \mid \theta\right)}{\sum_{k=1}^K P\left(\gamma_{j k}=1, y_j \mid \theta\right)} \\\\ &=\frac{P\left(y_j \mid \gamma_{j k}=1, \theta\right) P\left(\gamma_{j k}=1 \mid \theta\right)}{\sum_{k=1}^K P\left(y_j \mid \gamma_{j k}=1, \theta\right) P\left(\gamma_{j k}=1 \mid \theta\right)} \\\\ &=\frac{\alpha_k \phi\left(y_j \mid \theta_k\right)}{\sum_{k=1}^K \alpha_k \phi\left(y_j \mid \theta_k\right)}, \quad j=1,2, \cdots, N ; \quad k=1,2, \cdots, K \end{aligned} \]

\(\hat{\gamma}_{j k}\) 是在当前模型参数下第 \(j\) 个观测数据来自第 \(k\) 个分模型的概率, 称为分模型 \(k\) 对 观测数据 \(y_j\) 的响应度。 将 \(\hat{\gamma}_{j k}=E \gamma_{j k}\) 及 \(n_k=\sum_{j=1}^N E \gamma_{j k}\) 代入, 即得

\[ Q\left(\theta, \theta^{(i)}\right)=\sum_{k=1}^K\left\\{n_k \log \alpha_k+\sum_{j=1}^N \hat{\gamma}_{j k}\left[\log \left(\frac{1}{\sqrt{2 \pi}}\right)-\log \sigma_k-\frac{1}{2 \sigma_k^2}\left(y_j-\mu_k\right)^2\right]\right\\\} \]

3. 确定 EM 算法的 \(M\) 步 迭代的 \(\mathrm{M}\) 步是求函数 \(Q\left(\theta, \theta^{(i)}\right)\) 对 \(\theta\) 的极大值, 即求新一轮迭代的模型参数:

\[ \theta^{(i+1)}=\arg \max_\theta Q\left(\theta, \theta^{(i)}\right) \]

用 \(\hat{\mu}_k, \hat{\sigma}_k^2\) 及 \(\hat{\alpha}_k, k=1,2, \cdots, K\), 表示 \(\theta^{(i+1)}\) 的各参数。求 \(\hat{\mu}_k, \hat{\sigma}_k^2\) 只需分别对 \(\mu_k, \sigma_k^2\) 求偏导数并令其为 0 , 即可得到; 求 \(\hat{\alpha}_k\) 是在 \(\sum_{k=1}^K \alpha_k=1\) 条件 下求偏导数并令其为 0 得到的。结果如下:

\[ \begin{gathered} \hat{\mu}_k=\frac{\sum_{j=1}^N \hat{\gamma}_{j k} y_j}{\sum_{j=1}^N \hat{\gamma}_{j k}}, \quad k=1,2, \cdots, K \\\\ \hat{\sigma}_k^2=\frac{\sum_{j=1}^N \hat{\gamma}_{j k}\left(y_j-\mu_k\right)^2}{\sum_{j=1}^N \hat{\gamma}_{j k}}, \quad k=1,2, \cdots, K \\\\ \hat{\alpha}_k=\frac{n_k}{N}=\frac{\sum_{j=1}^N \hat{\gamma}_{j k}}{N}, \quad k=1,2, \cdots, K \end{gathered} \]

重复以上计算, 直到对数似然函数值不再有明显的变化为止。 现将估计高斯混合模型参数的 EM算法总结如下。

算法应用总结

(高斯混合模型参数估计的EM算法) 输入: 观测数据 \(y_1, y_2, \cdots, y_N\), 高斯混合模型; 输出：高斯混合模型参数。 （1）取参数的初始值开始迭代; (2) \(\mathrm{E}\) 步: 依据当前模型参数, 计算分模型 \(k\) 对观测数据 \(y_j\) 的响应度

\[ \hat{\gamma}_{j k}=\frac{\alpha_k \phi\left(y_j \mid \theta_k\right)}{\sum_{k=1}^K \alpha_k \phi\left(y_j \mid \theta_k\right)}, \quad j=1,2, \cdots, N ; \quad k=1,2, \cdots, K \]

3. \(\mathrm{M}\) 步：计算新一轮迭代的模型参数

\[ \hat{\mu}_k=\frac{\sum_{j=1}^N \hat{\gamma}_{j k} y_j}{\sum_{j=1}^N \hat{\gamma}_{j k}}, \quad k=1,2, \cdots, K \]

\[ \hat{\sigma}_k^2=\frac{\sum_{j=1}^N \hat{\gamma}_{jk}(y_j-\mu_k)^2}{\sum_{j=1}^N \hat{\gamma}_{jk}}, \quad k= 1,2,\dots, K \]

\[ \hat{\alpha}_k = \frac{\sum_{j=1}^N \hat{\gamma}_{jk}}{N} ,\quad k=1,2,\dots, K \]

4. 重复直到收敛。

总结

总之来说em算法作为数据挖掘十大算法之一，应用范围十分广泛，它不能看作是一个具体的模型，常常用于模型的求解，比如HMM的学习参数问题等等，是必须要学会的算法之一。