DBSCAN

DBSCAN属于密度聚类的一种。通常情形下，密度聚类算法从样 本密度的角度来考察样本之间的可连接性，并基于可连接样本不断扩展聚类簇 以获得最终的聚类结果。

DBSCAN基于一组“邻域”参数\((\epsilon, Minpts)\)来刻画样本分布的紧密程度，给定数据集\(D=\\{x_1,x_2, \dots,x_m \\}\)，定义几个概念：

• \(\epsilon\)-邻域：对\(x_j\in D\)，其\(\epsilon\)-邻域包含样本集D中与\(x_j\)的距离不大于\(\epsilon\)的样本，即\(N_{\epsilon}(x_j) = \\{dist(x_i, x_j) \leq \epsilon\\}\)。
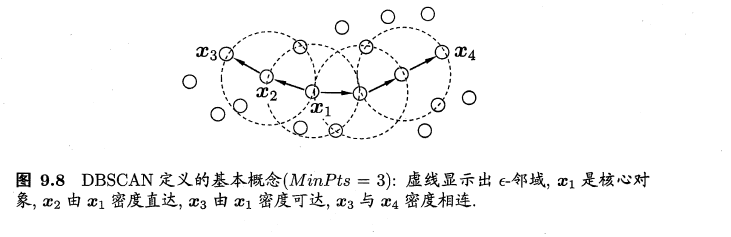
• 核心对象 (core object): 若 \(x_j\) 的 \(\epsilon\)-邻域至少包含 MinPts 个样本, 即 \(\left|N_\epsilon\left(\boldsymbol{x}_j\right)\right| \geqslant \operatorname{MinPts}\), 则 \(\boldsymbol{x}_j\) 是一个核心对象;
• 密度直达(directly density-reachable): 若 \(\boldsymbol{x}_j\) 位于 \(\boldsymbol{x}_i\) 的 \(\epsilon\)-邻域中, 且 \(\boldsymbol{x}_i\) 是 核心对象, 则称 \(\boldsymbol{x}_j\) 由 \(\boldsymbol{x}_i\) 密度直达;
• 密度可达(density-reachable): 对 \(\boldsymbol{x}_i\) 与 \(\boldsymbol{x}_j\), 若存在样本序列 \(\boldsymbol{p}_1, \boldsymbol{p}_2, \ldots, \boldsymbol{p}_n\), 其中 \(\boldsymbol{p}_1=\boldsymbol{x}_i, \boldsymbol{p}_n=\boldsymbol{x}_j\) 且 \(\boldsymbol{p}_{i+1}\) 由 \(\boldsymbol{p}_i\) 密度直达, 则称 \(\boldsymbol{x}_j\) 由 \(\boldsymbol{x}_i\) 密度可达;
• 密度相连 (density-connected): 对 \(\boldsymbol{x}_i\) 与 \(\boldsymbol{x}_j\), 若存在 \(\boldsymbol{x}_k\) 使得 \(\boldsymbol{x}_i\) 与 \(\boldsymbol{x}_j\) 均由 \(\boldsymbol{x}_k\) 密度可达, 则称 \(\boldsymbol{x}_i\) 与 \(\boldsymbol{x}_j\) 密度相连.

既然是聚类，那就要定义簇的概念