B树

B树就是B-树，以前还以为这是两种树，现在才知道这俩就是一个东西。

基本概念

1. 所有的叶子结点都出现在同一层上，并且不带信息(可以看做是外部结点或查找失败的结点，实际上这些结点不存在，指向这些结点的指针为空)。
2. 每个结点包含的关键字个数有上界和下界。用一个被称为 B-树的 最小度数 的固定整数 t≥2 来表示这些界 ，其中 t 取决于磁盘块的大小：
   a.除根结点以外的每个结点必须至少有 t−1 个关键字。因此，除了根结点以外的每个内部结点有 t 个孩子。如果树非空，根结点至少有一个关键字。
   2. 每个结点至多包含 2t−1 个关键字。
3. 一个包含x个关键字的结点有x+1个孩子。
4. 一个结点中所有的关键字升序排列，两个关键字\(k_1\)和\(k_2\)之间的孩子结点的所有关键字key在\((k_1, k_2)\)的范围内。

其中最小度数和B树的阶不一样：

度：一个结点含有的子结点的个数称为该结点的度
阶：一棵树的最大孩子数

最小度minimum degree（t）：用来衡量结点的关键字数量范围
阶 order（m）：衡量B树中的结点的最大孩子数

关系如下：

\[ t = ceil(\frac{m}{2}) \quad m = 2t \] 可以简单理解为最小度是孩子数的最小值，阶是孩子数的最大值。最小度-1是节点关键字数的最小值，阶-1是节点关键字数的最大值。

查找

查找很简单，对每个键中的索引进行比较然后查找就可以。

插入

伪代码：

1. 初始化 x 作为根结点
2. 当 x 不是叶子结点，执行如下操作：

• 找到 x 的下一个要被访问的孩子结点 y
• 如果 y 没有满，则将结点 y 作为新的 x
• 如果 y 已经满了，拆分 y ，结点 x 的指针指向结点 y 的两部分。 如果 k 比 y 中间的关键字小， 则将 y 的第一部分作为新的 x ，否则将 y 的第二部分作为新的 x ，当将 y 拆分后，将 y 中的一个关键字移动到它的父结点 x 当中。

1. 当 x 是叶子结点时，第二步结束； 由于我们已经提前查分了所有结点，x 必定至少有一个额外的关键字空间，进行简单的插入即可。

删除

1. 待删除的关键字 k 在结点 x 中，且 x 是叶子结点，删除关键字k
2. 待删除的关键字 k 在结点 x 中，且 x 是内部结点，分一下三种情况 1). 如果位于结点 x 中的关键字 k 之前的第一个孩子结点 y 至少有 t 个关键字，则在孩子结点 y 中找到 k 的前驱结点 k0 ，递归地删除关键字 k0 ，并将结点 x 中的关键字 k 替换为 k0

直接前驱：当前关键字左侧指针 所指子树中“最右下”的元素

删除 B-树中的关键字 G ，G 的前一个孩子结点 y 为 [D、E、F] ，包含 3个关键字，满足情况一，关键字 G 的直接前驱为关键 F ，删除 F ，然后将 G 替换为 F .

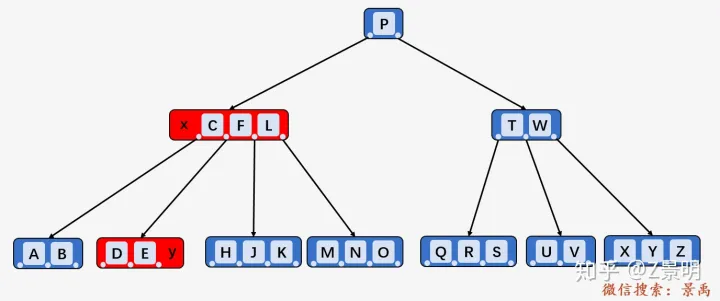
2).y 所包含的关键字少于 t 个关键字，则检查结点 x 中关键字 k 的后一个孩子结点 z 包含的关键字的个数，如果 z 包含的关键字的个数至少为 t 个，则在 z 中找到关键字 k 的直接后继 K0 ,然后删除 K0 ，并将关键 k 替换为 K0 .

直接后继：当前关键字右侧指针 所指子树中“最左下”的元素

删除 B-树中的关键字 C , y 中包含的关键字的个数为 2 个，小于 t = 3 ,结点 [C、G、L] 中的 关键字 C 的后一个孩子 z 为 [D、E、F] 包含 3 个关键字，关键字 C 的直接后继为 D ，删除 D ，然后将 C 替换为 D .

3). 如果 y 和 z 都只包含 t -1 个关键字，合并关键字 k 和所有 z 中的关键字到 结点 y 中，结点 x 将失去关键字 k 和孩子结点 z，y 此时包含 2t -1 个关键字，释放结点 z 的空间并递归地从结点 y 中删除关键字 k.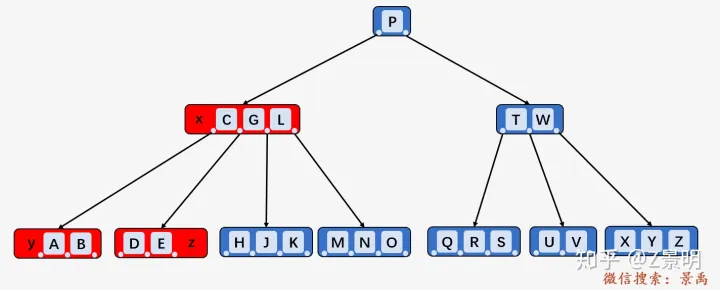

删除关键字 C , 结点 y 包含 2 个关键字 ，结点 z 包含 2 个关键字，均等于 t - 1 = 2 个， 合并关键字 C 和结点 z 中的所有关键字到结点 y 当中：

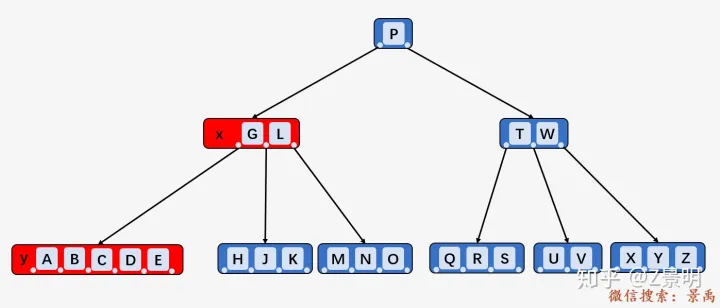
之后直接删除C即可。

3. 如果关键字 k 不在当前在内部结点 x 中，则确定必包含 k 的子树的根结点 x.c(i) （如果 k 确实在 B-树中）。如果 x.c(i) 只有 t - 1 个关键字，必须执行下面两种情况进行处理：

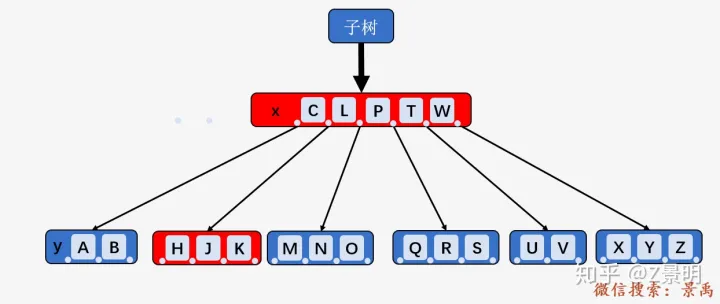
首先我们得确认什么是当前内部结点 x ，什么是 x.c(i) ,如下图所示， P 现在不是根结点，而是完整 B-树的一个子树的根结点：

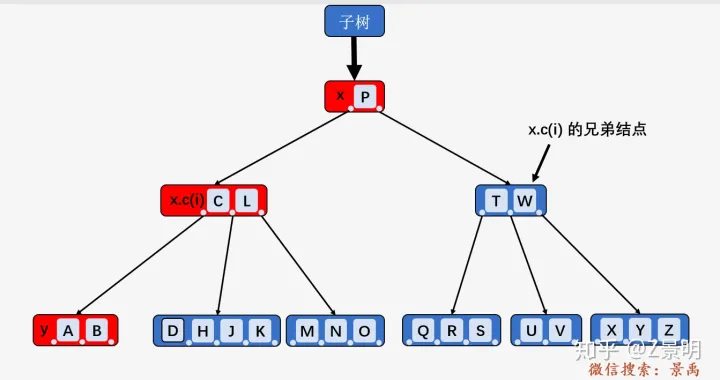
1). x.c(i) 仅包含 t - 1 个关键字且 x.c(i) 的一个兄弟结点包含至少 t 个关键字，则将 x 的某一个关键字下移到 x.c(i) 中，将 x.c(i) 的相邻的左兄弟或右兄弟结点中的一个关键字上移到 x 当中，将该兄弟结点中相应的孩子指针移到 x.c(i) 中，使得 x.c(i) 增加一个额外的关键字。

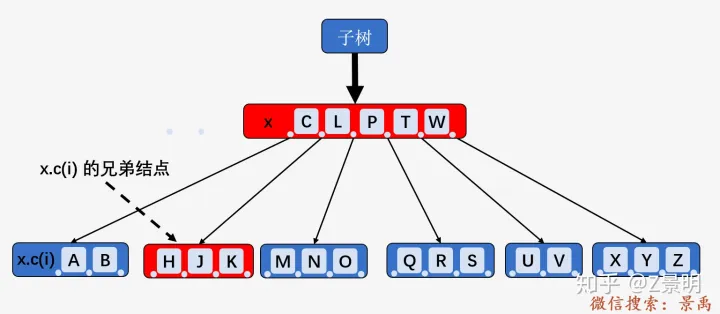
我们以删除结点 [A、B] 中的结点 B 为例，上图中 x.c(i) 包含 2 个关键字，即 t - 1 个关键字， x.c(i) 的一个兄弟结点 [H、J、K] 包含 3 个关键字（满足至少 t 个关键字的要求），则将兄弟结点 [H、J、K] 中的关键字 H 向上移动到 x 中， 将 x 中的关键字 C 下移到 x.c(i) 中；删除关键字 B .

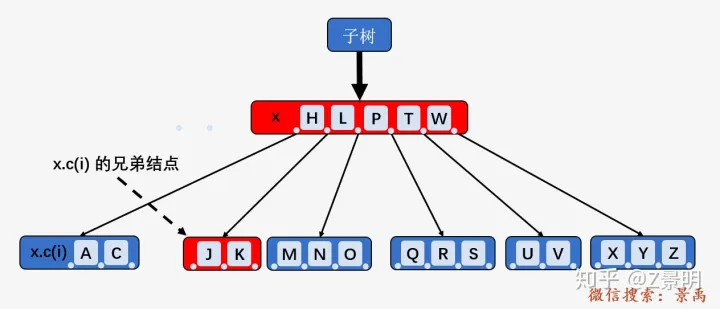
2).如果 x.c(i) 及 x.c(i) 的所有相邻兄弟都只包含 t - 1 个关键字，则将 x.c(i) 与 一个兄弟合并，即将 x 的一个关键字移动至新合并的结点，使之成为该结点的中间关键字，将合并后的结点作为新的 x 结点 .

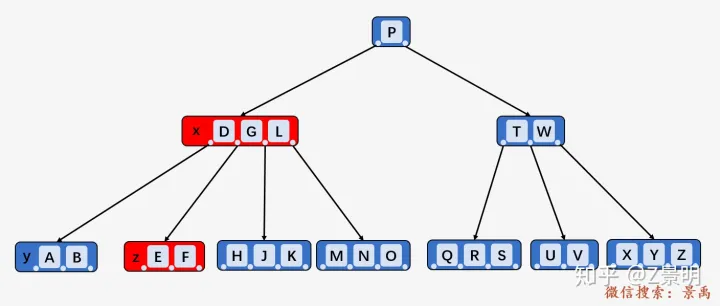
以此图为例：

上面的图标明了相应的 x 及 x.c(i) ，我们以删除关键字 D 为例，此时当前内部结点 x 不包含关键字 D , 确定是第三种情况，我们可以确认关键 D 一定在结点 x 的第一个孩子结点所在的子树中，结点 x 的第一个孩子结点所在子树的跟结点为 x.c(i) 即 [C、L] . 其中 结点 [C、L] 及其相邻的兄弟结点 [T、W] 都只包含 2 个结点（即 t - 1) ，则将 [C、L] 与 [T、W] 合并，并将结点 x 当中仅有的关键字 P 合并到新结点中；然后将合并后的结点作为新的 x 结点，递归删除关键字 D ，发现D 此时在叶子结点 y 中，直接删除，就是 1. 的情况。