Seq2Seq中的Attention

缺陷

在seq2seq这篇文章中详细介绍了seq2seq模型的细节，但是仅仅用一个语义编码c是完全不能够表示编码器的输入的，源的可能含义的数量是无限的。当编码器被迫将所有信息放入单个向量中时，它很可能会忘记一些东西。

不仅编码器很难将所有信息放入一个向量中——这对解码器来说也很困难。解码器只看到源的一种表示。但是，在每个生成步骤中，源的不同部分可能比其他部分更有用。但在目前的情况下，解码器必须从相同的固定表示中提取相关信息——这不是一件容易的事。

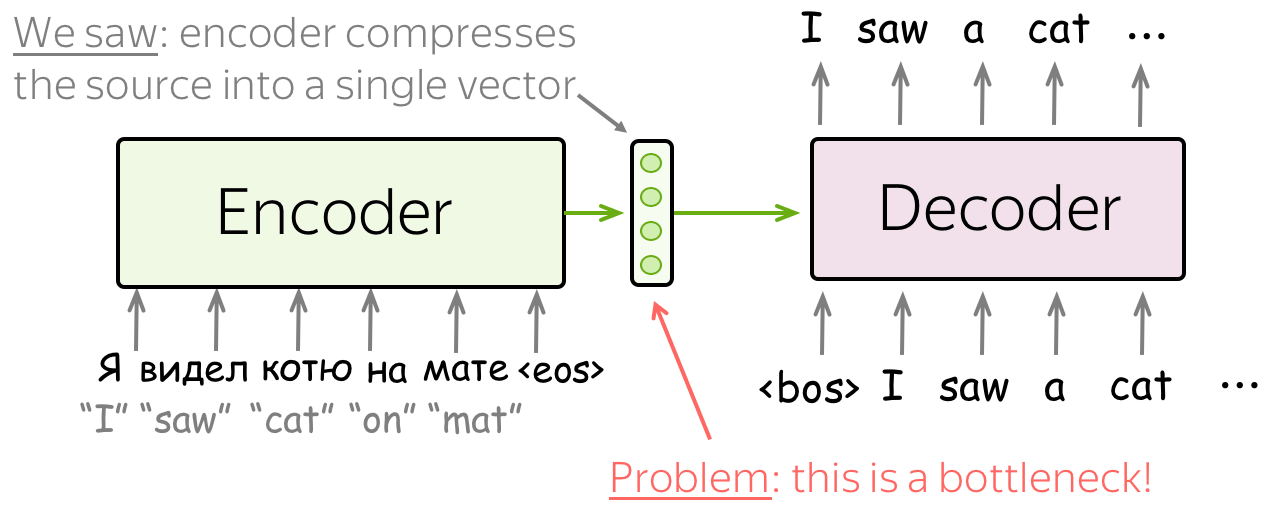
这个时候就需要引入注意力机制了，注意这里的注意力机制和transformer中的self-attention是不一样的。下面详细介绍一下。注意几个名词：注意力得分、注意力权重。其中注意力得分即score的计算有多种方法，权重就是对得分进行softmax归一化。

attention

注意机制是神经网络的一部分。在每个解码器步骤中，它决定哪些源部分更重要。在此设置中，编码器不必将整个源压缩为单个向量 - 它为所有源标记提供表示（例如，所有 RNN 状态而不是最后一个）。

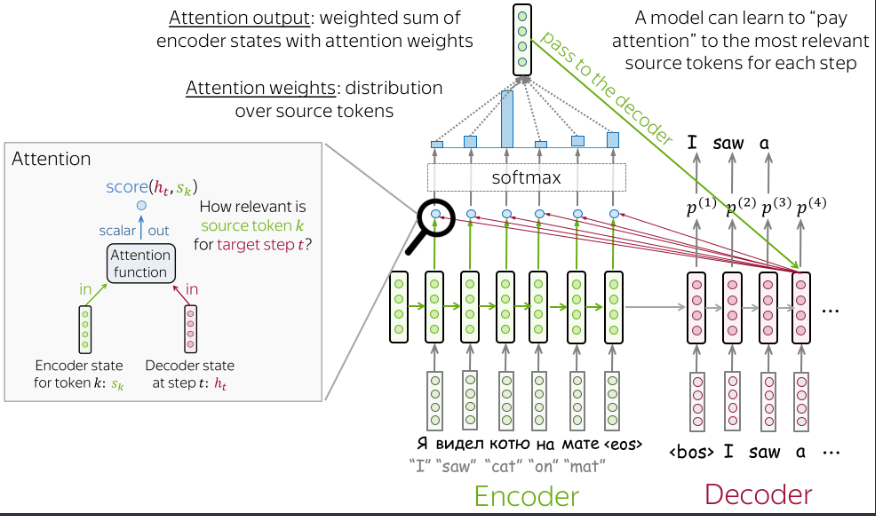步骤： - 接受注意输入：解码器状态\(h_t\)以及所有编码器状态\(s_1,s_2,\dots,s_m\) - 计算每个编码器状态的注意力分数\(s_k\)，注意力分数表示它对解码器状态\(h_t\)的相关性，使用注意力函数，接收一个解码器状态和一个编码器状态并返回一个标量分数，即图中的\(score(h_t,s_k)\) - 计算注意力权重：即概率分布- 使用Softmax函数 - 计算注意力输出：具有注意力机制的编码器状态的加权和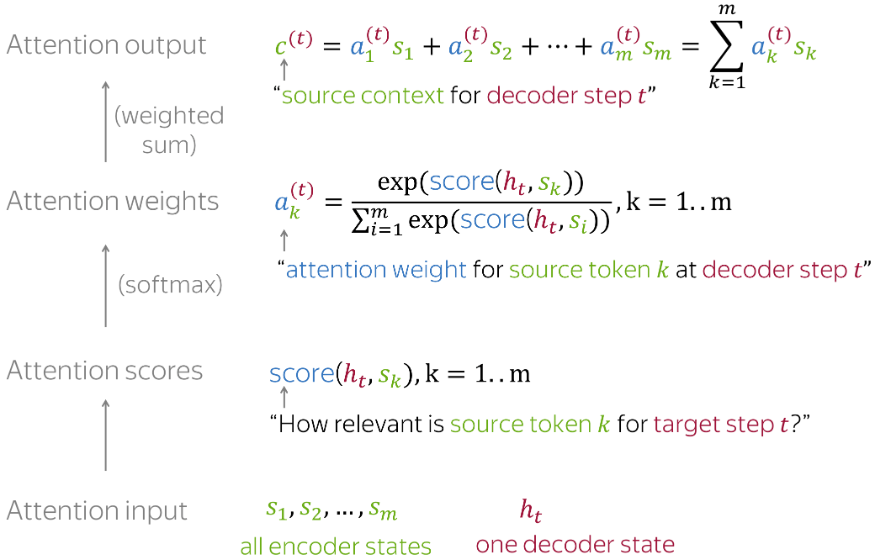

即为如图所示内容为如何计算注意力。

注意我们提到的注意力函数，这里的注意力分数的计算有很多种方法，下面介绍几种比较常见的办法： - 点积： 最简单的办法。 - 双线性函数 - 多层感知机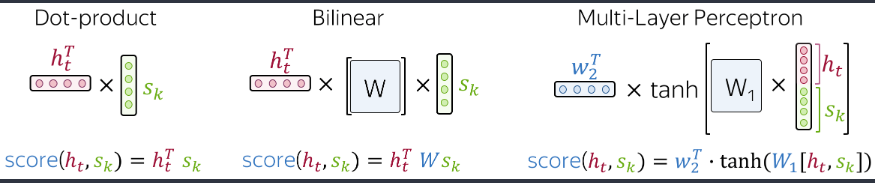

注意后两者都有要优化的参数的，第一个点积是直接运算，因此很简单。 在应用时可以直接将注意力的结果传输到最后的softmax，也可以将原始的\(h_t\)合并，下面介绍几种变体。

Bahdanau Model

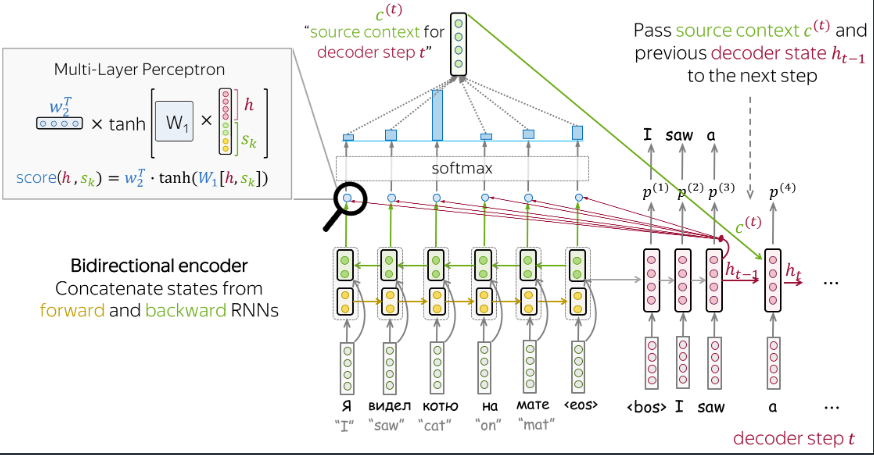- 编码器使用双向的RNN - 利用上一时刻的隐层状态计算注意力输出c，然后和隐层状态一起作为当前时刻的输入，再得到结果\(\hat{y}\)。这里再说一下训练的过程中当前步的输入使用的是真实的\(y\)，测试的时候才会使用上一步的输出作为输入。可以将上下文向量c（也就是注意力输出）与\(x\)拼接后作为输入。 - 注意力得分使用的是感知机。 这里引用一下李沐大佬的代码：

class Seq2SeqAttentionDecoder(AttentionDecoder):

    def __init__(self, vocab_size, embed_size, num_hiddens, num_layers,

                 dropout=0, **kwargs):

        super(Seq2SeqAttentionDecoder, self).__init__(**kwargs)

        self.attention = d2l.AdditiveAttention(

            num_hiddens, num_hiddens, num_hiddens, dropout)

        self.embedding = nn.Embedding(vocab_size, embed_size)

        self.rnn = nn.GRU(

            embed_size + num_hiddens, num_hiddens, num_layers,

            dropout=dropout)

        self.dense = nn.Linear(num_hiddens, vocab_size)

  

    def init_state(self, enc_outputs, enc_valid_lens, *args):

        # outputs的形状为(batch_size，num_steps，num_hiddens).

        # hidden_state的形状为(num_layers，batch_size，num_hiddens)

        outputs, hidden_state = enc_outputs

        return (outputs.permute(1, 0, 2), hidden_state, enc_valid_lens)

  

    def forward(self, X, state):

        # enc_outputs的形状为(batch_size,num_steps,num_hiddens).

        # hidden_state的形状为(num_layers,batch_size,

        # num_hiddens)

        enc_outputs, hidden_state, enc_valid_lens = state

        # 输出X的形状为(num_steps,batch_size,embed_size)

        X = self.embedding(X).permute(1, 0, 2) # 转换是为了方便后面循环计算。

        outputs, self._attention_weights = [], []

        for x in X:

            # query的形状为(batch_size,1,num_hiddens)

            query = torch.unsqueeze(hidden_state[-1], dim=1) # -1是指在最后一层最后时刻的隐藏状态，作为query

            # context的形状为(batch_size,1,num_hiddens)

            context = self.attention(

                query, enc_outputs, enc_outputs, enc_valid_lens)

            # 在特征维度上连结

            x = torch.cat((context, torch.unsqueeze(x, dim=1)), dim=-1)

            # 将x变形为(1,batch_size,embed_size+num_hiddens)

            out, hidden_state = self.rnn(x.permute(1, 0, 2), hidden_state)

            outputs.append(out)

            self._attention_weights.append(self.attention.attention_weights)

        # 全连接层变换后，outputs的形状为

        # (num_steps,batch_size,vocab_size)

        outputs = self.dense(torch.cat(outputs, dim=0))

        return outputs.permute(1, 0, 2), [enc_outputs, hidden_state,

                                          enc_valid_lens]

  

    @property

    def attention_weights(self):

        return self._attention_weights

Luong Model

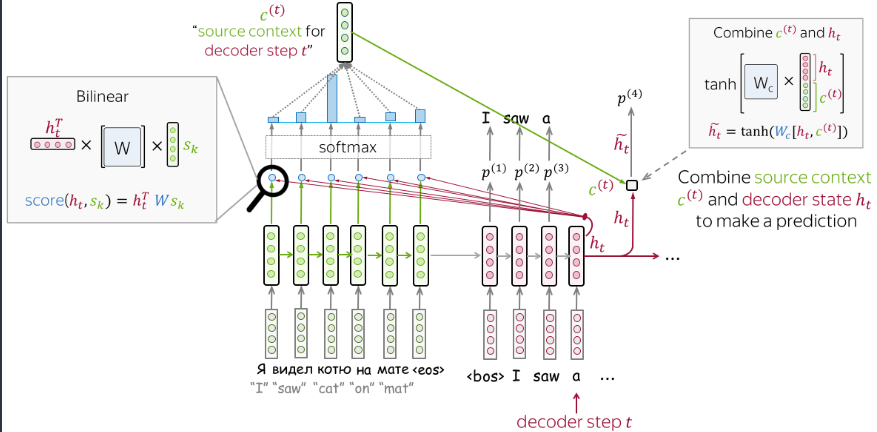这个模型的编码器比较常规，使用当前状态计算注意力输出，然后解码器中将隐层状态与注意力输出做一步结合，这样得到了新的隐层状态，然后再传递得到预测结果。

注意力对齐

可以看到解码器关注的源token。

到此seq2seq中的attention就介绍完毕了，其实还有很多细节，以后遇到了会持续补充。

Self-attention

移步transformer。Transformer

KV cache

KV cache # MQA

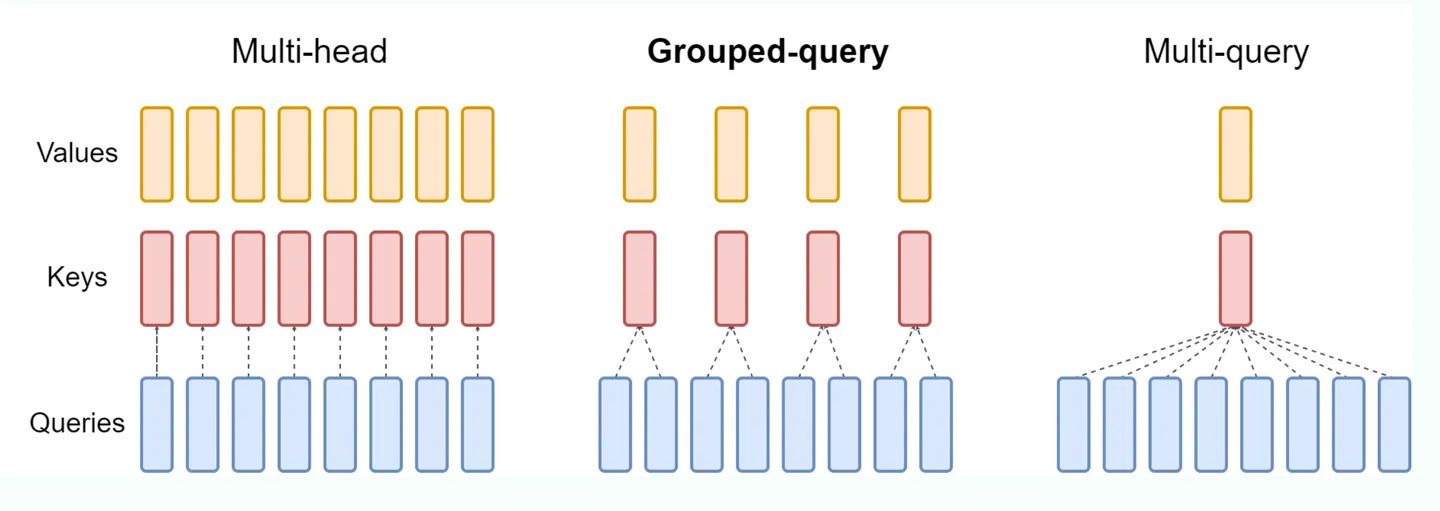
标准的mha中，KV heads的数量和Query heads的数量相同，每一个q head对应一个独立的kv head，但这样的开销比较大。 MQA (Multi Queries Attention): MQA比较极端，只保留一个KV Head，多个Query Heads共享相同的KV Head。这相当于不同Head的Attention差异，全部都放在了Query上，需要模型仅从不同的Query Heads上就能够关注到输入hidden states不同方面的信息。这样做的好处是，极大地降低了KV Cache的需求，但是会导致模型效果有所下降。（层内共享） # GQA 如上图所示，GQA就是在MHA和MQA之间做了一个平衡。对query heads进行分组，分成几组就对应多少个kv heads，然后每一组内的query Heads共享相同的KV head。 GQA可以在减少计算量和KV Cache同时确保模型效果不受到大的影响。 # online attention ### 3-pass \(\mathsf{NO}\)TATIONS

\(\{m_i\}{:}\max_{j=1}^i\left\{x_j\right\}\), with initial value \(m_0=-\infty.\) \(\{d_i\}{:}\sum_{j=1}^ie^{x_j-m_N}\), with initial value \(d_0=0,d_N\) is the denominator of safe softmax. \(\{a_i\}{:\text{ the final softmax value}}.\)

BODY \(\textbf{for }i\leftarrow 1, N\textbf{ do}\) \[m_i\leftarrow\max\left(m_{i-1},x_i\right)\] \(\mathbf{end}\)

\(\textbf{for }i\leftarrow 1, N\textbf{ do}\) \[d_i\leftarrow d_{i-1}+e^{x_i-m_N}\] \(\mathbf{end}\)

\(\textbf{for }i\leftarrow 1, N\textbf{ do}\) \[a_i\leftarrow\frac{e^{x_i-m_N}}{d_N}\] \(\mathbf{end}\)

这是3step计算attention的方法，每一步都需要上一步的结果才可以继续计算。这样的话由于sram中没有足够的存储空间，因此需要多次访存。 ### online attention \[\begin{aligned} d_i^{\prime}& =\sum_{j=1}^ie^{x_j-m_i} \\ &= \left(\sum_{j=1}^{i-1} e^{x_j-m_i}\right)+e^{x_i-m_i} \\ &= \left(\sum_{j=1}^{i-1} e^{x_j-m_{i-1}}\right)e^{m_{i-1}-m_i}+e^{x_i-m_i} \\ &= d_{i-1}' e^{m_{i-1}-m_i}+e^{x_i-m_i} \end{aligned}\] 找到迭代式之后就可以从3step降到2step \[\begin{aligned}&\mathbf{for~}i\leftarrow1,N\textbf{ do}\\&&&m_i&&\leftarrow&\max\left(m_{i-1},x_i\right)\\&&&d_i^{\prime}&&\leftarrow&d_{i-1}^{\prime}e^{m_{i-1}-m_i}+e^{x_i-m_i}\\&\mathbf{end}\\&\mathbf{for~}i\leftarrow1,N\textbf{ do}\\&&&a_i\leftarrow&&\frac{e^{x_i-m_N}}{d_N^{\prime}}\\&\mathbf{end}\end{aligned}\] 好像FLOPs计算量并没有减少，甚至还略有增加，因为现在每次都需要计算额外的scale

x值，也就是pre-softmax logits，由于需要O(N^2)的显存无法放在SRAM中。因此：
1. 要么提前计算好x，保存在全局显存中，需要O(N^2)的显存，容易爆显存。
2. 要么在算法中online计算，每次循环中去load一部分Q，K到片上内存，计算得到x。

Attention优化的目标就是避开第一种情况，尽可能节省显存，否则，LLM根本无法处理类似100K以上这种long context的情况。而对于第二种情况，我们不需要保存中间矩阵x，节省了显存，但是计算没有节省，并且增加了HBM IO Accesses（需要不断地load Q, K）。此时，2-pass算法相对于3-pass算法，可以减少一次整体的load Q, K以及减少一次对 xi 的online recompute，因为在2-pass的第一个pass中， xi 是被两次计算共享的。类似online-softmax这种算法，对应到Attention中的应用，就是Memory Efficient Attention（注意不是FlashAttention）。 # flash attention safe softmax并没有1-pass算法，那么Attention会不会有呢？有！这就是FlashAttention！

在使用online attention的情况下，从头开始计算attention score的过程如下： \(\operatorname{NOTATIONS}\)

\(Q[k,:]:\)the \(k\)-th row vector of \(Q\) matrix. \(\begin{aligned}O[k,:]:\mathrm{~the~}k\text{-th row of output }O\mathrm{~matrix.}\\\mathbf{V}[i,i]:\mathrm{~the~}k\text{-th row of output }O\mathrm{~matrix.}\end{aligned}\) \(V[i,:]{:\text{ the }i\text{-th row of }V\text{ matrix}}.\) \(\{\boldsymbol{o}_i\}{:}\sum_{j=1}^ia_jV[j,:]\), a row vector storing partial aggregation result \(A[k,:i]\times V[:i,:]\) BODY

\(\textbf{for }i\leftarrow 1, N\textbf{ do}\) \[\begin{aligned}x_i&\leftarrow\quad Q[k,:]\:K^T[:,i]\\m_i&\leftarrow\quad\max\left(m_{i-1},x_i\right)\\d_i'&\leftarrow\quad d_{i-1}'e^{m_{i-1}-m_i}+e^{x_i-m_i}\end{aligned}\] \(\mathbf{end}\)

\(\textbf{for }i\leftarrow 1, N\textbf{ do}\) \[\begin{aligned}&a_i\:\leftarrow\:\frac{e^{x_i-m_N}}{d_N^{\prime}}\\&o_i\:\leftarrow\:o_{i-1}+a_i\:V[i,:\:]\end{aligned}\] \(\mathbf{end}\) \[O[k,:]\leftarrow\boldsymbol{o}_N\]

优化思路和online attention一样，将\(o_{i}\)的计算简化以便于可以写成迭代式。

原来的\(o_{i}\)使用以下方式计算，依赖于全局的\(m_{N}\)和\(d_{N}\)。 \[\boldsymbol{o}_i:=\sum_{j=1}^i\left(\frac{e^{x_j-m_N}}{d_N^{\prime}}V[j,:]\right)\] 将其改写成如下形式： \[\boldsymbol{o}_i^{\prime}:=\left(\sum_{j=1}^i\frac{e^{x_j-m_i}}{d_i^{\prime}}V[j,:]\right)\] 这样按照上面的方式拓展下去，可以找到一个循环迭代式。

\[\begin{aligned} \mathbf{o}_i^{\prime}& =\sum_{j=1}^i\frac{e^{x_j-m_i}}{d'}V[j,:] \\ &= \left(\sum_{j=1}^{i-1}\frac{e^{x_j-m_i}}{d_i^{\prime}}V[j,:] \right)+\frac{e^{x_i-m_i}}{d_i^{\prime}}V[i,:] \\ &= \left(\sum_{j=1}^{i-1}\frac{e^{x_j-m_{i-1}}}{d_{i-1}^{\prime}}\frac{e^{x_j-m_i}}{e^{x_j-m_{i-1}}}\frac{d_{i-1}^{\prime}}{d_i^{\prime}}V[j,:]\right)+\frac{e^{x_i-m_i}}{d_i^{\prime}}V[i,:] \\ &= \left(\sum_{j=1}^{i-1}\frac{e^{x_j-m_{i-1}}}{d_{i-1}^{\prime}}V[j,.]\right)\frac{d_{i-1}^{\prime}}{d_i^{\prime}}e^{m_{i-1}-m_i}+\frac{e^{x_i-m_i}}{d_i^{\prime}}V[i,.] \\ &= \boldsymbol{o}_{i-1}'\frac{d_{i-1}'e^{m_{i-1}-m_i}}{d_i'}+\frac{e^{x_i-m_i}}{d_i'}V[i,:] \end{aligned}\]

这样就找到了\(o_{i}\)的递推表达式。

之后对Q,K进行tiling后计算，得到如下： \[\begin{aligned}&\textbf{for }i\leftarrow1,\#\text{tiles do}\\&&&\boldsymbol{x}_i\quad\leftarrow\quad Q[k;\cdot] K^T[\cdot,(i-1) b; i b]\\&&&m_i^{(\mathrm{local})}=\begin{array}{c}\overset{b}{\operatorname*{max}}\left(\boldsymbol{x}_i[j]\right)\\\end{array}\\&&&m_i \leftarrow \max\left(m_{i-1},m_i^{(\mathrm{local})}\right)\\&&&a_i^{\prime} \leftarrow d_{i-1}^{\prime}e^{m_{i-1}-m_i}+\sum_{j=1}^be^{\boldsymbol{x}_i[j]-m_i}\\&&&\boldsymbol{o}_i^{\prime} \leftarrow \boldsymbol{o}_{i-1}^{\prime}\frac{d_{i-1}^{\prime}e^{m_{i-1}-m_i}}{d_i^{\prime}}+\sum_{j=1}^b\frac{e^{\boldsymbol{x}_i[j]-m_i}}{d_i^{\prime}}V[(i-1) b+j,:]\\&\text{end}\\&&&O[k,:]\leftarrow\boldsymbol{o}_{N/b}^{\prime}\end{aligned}\] 对于tiles，示意图如下：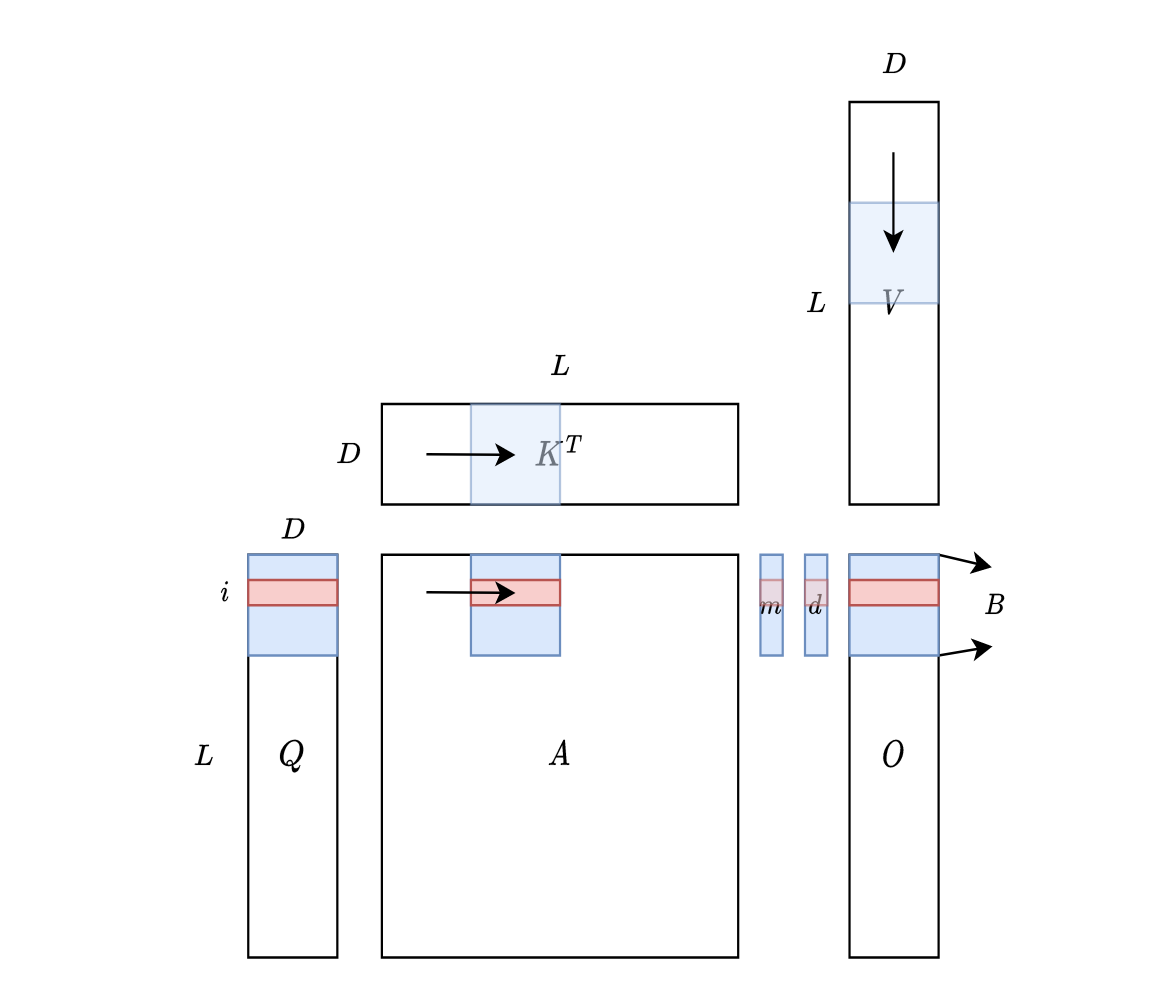

可以理解成滑动窗口，\(K^{T}\)从左向右滑动（按列读取），\(V\)从上向下滑动（按行读取）。也可以直接理解成分块矩阵，具体为什么这么做，参考：Cuda 编程之 Tiling - 知乎 (zhihu.com) # 参考

[KV Cache优化]🔥MQA/GQA/YOCO/CLA/MLKV笔记: 层内和层间KV Cache共享 - 知乎 (zhihu.com)

Transformers KV Caching Explained | by João Lages | Medium

From Online Softmax to FlashAttention. https://courses.cs.washington.edu/courses/cse599m/23sp/notes/flashattn.pdf