as_strided

调用为np.lib.stride_tricks.as_strided() 可以分割一个数组为不同的shape块，有个问题就是什么是strides呢？可以看个例子：

a = np.arange(9, dtype=np.int32).reshape(3,3)
print(a)
'''
[[0 1 2]
 [3 4 5]
 [6 7 8]]
 '''
print(a.strides)
'''
(12, 4)
'''

这里（12， 4）中的12表示在内存中a[n, 0]到a[n+1, 0]跨过多少byte，4表示在内存中a[n, 0]到a[n, 1]跨过多少byte。

32int需要4byte是众所周知。

看一下函数的参数：

numpy.lib.stride_tricks.as_strided(x, shape=None, strides=None, subok=False, writeable=True)

x就是我们要分割的矩阵，可以当做是一个蓝图，shape，strides都是新矩阵的属性，也就是说这个函数按照给定的shape和strides来划分x，返回一个新的矩阵。

对于X：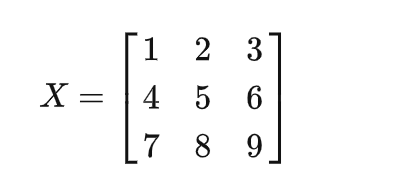

如果卷积核的大小是2x2，stride为1，那么就需要把矩阵X转换为包含如下4个小矩阵的新矩阵A：

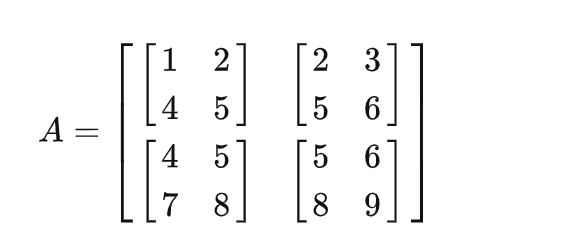
很明显A的维度为(2,2,2,2)。

所以shape可以确定，但strides还不确定：

A = as_strided(X, shape=(2,2,2,2), strides)

下面确定strides，从图中可以确定最低维的为4，因为所有数据都在X上，所以A的各个维度的跨度都要根据X来确定，而不是A中，以1和4为例子，在X中的距离为12字节，所以现在可以确定后两维：（?,?,12,4）。 再看更高维度: 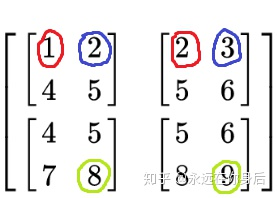从X中可以看到，第二维的距离为4。 第一维也不多说，是12。 最后可以strides =（12，4，12，4）。

这就是整个分析的过程，可以方便卷积操作，不是嘛。

再看一个例子就结束了，估计以后会忘，记录下来。

意思就是将一个向量拓展成这样的形式，用循环的方法很容易实现：

def sliding_stack_py(v, k):

    "Stack sliding windows of v of length k."

    rows = []

    for i in range(len(v) - k + 1):

        rows.append(v[i : (i + k)])

    return np.array(rows)

但如果不能使用循环呢，就可以用刚说的这个函数了:

def sliding_stack_np(v, k):

    return np.lib.stride_tricks.as_strided(v, shape=(len(v) - k + 1, k), strides=(v.strides[0], v.strides[0]))

因为原向量是1维的，所以转换后的strides为[4,4]。希望可以帮助理解。