Adaboost

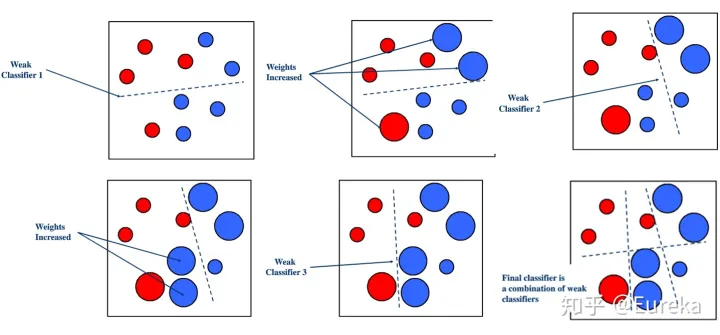
Boosting算法的工作机制是首先从训练集用初始权重训练出一个弱学习器1，根据弱学习的学习误差率表现来更新训练样本的权重，使得之前弱学习器1学习误差率高的训练样本点的权重变高，使得这些误差率高的点在后面的弱学习器2中得到更多的重视。然后基于调整权重后的训练集来训练弱学习器2.，如此重复进行，直到弱学习器数达到事先指定的数目T，最终将这T个弱学习器通过集合策略进行整合，得到最终的强学习器。

这段叙述里面有很多需要解决的东西，比如如何计算误差率，如何得到弱学习器权重系数，如何更新样本权重，如何结合。

Adaboost

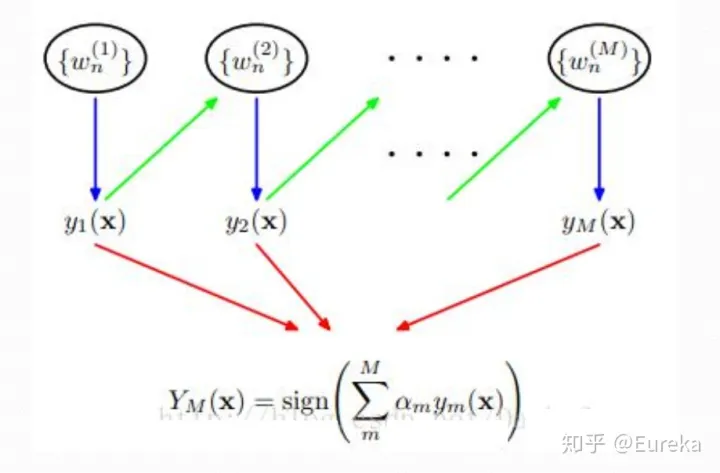
先看一下adaboost的算法流程

将初始化样本的权重为\(\frac{1}{m}\)，那么这个样本权重到底怎么用呢，主要是用于在构建弱分类器时计算弱学习器在训练集上的误差时使用，也就是计算误差：

\[ \epsilon_t = \sum_{i=1}^mP(h_t(x_i) \neq y_i) =\sum_{i=1}^m D_{ti}I(h_t(x_i)\neq y_i) \]

如果弱分类器为决策树的话，肯定要选择误差最小的划分作为最佳划分，最小的误差最为本轮弱分类器的误差。实际上样本权重不参与训练，只是通过样本权重动态调节模型的关注重点，即通过计算误差，影响决策树的划分，来调节模型的关注重点，这就是样本权重的作用。

然后计算弱学习器权重\(\alpha_t\)，更新样本权重，对于分类错误的样本权重上升，对于分类正确的样本权重下调，再除以规范化因子，确保仍然是一个分布，一般就是\(D_t\)的和作为规范化因子，下一轮的模型就更注意划分错误的这些样本点。这样每一轮迭代都会得到弱分类器系数和弱分类器，这里具体的计算过程可以参考李航的《统计学习方法》，迭代完成以后，按照公式将权重与弱分类器相乘后相加，最后经过信号函数得到最终的分类结果。 ## 优点

1. Adaboost作为分类器时，分类精度很高
   
2. 在Adaboost的框架下，可以使用各种回归分类模型来构建弱学习器，非常灵活。
   
3. 作为简单的二元分类器时，构造简单，结果可理解。
   
4. 不容易发生过拟合

缺点

对异常样本敏感，异常样本在迭代中可能会获得较高的权重，影响最终的强学习器的预测准确性。

另一种解释

上面叙述的是一般的Adaboost算法的解释，其实还有另外一种解释，就是adaboost为加法模型、损失函数为指数函数、学习算法为前向分步算法的二类分类学习方法。 那么什么是前向分步算法？

输入: 训练数据集\(T=\{(x_1, y_1 ),(x_2, y_2), \cdots,\left(x_N, y_N\right)\}\); 损失函数 \(L(y, f(x))\); 基函数集 \(\{b(x ; \gamma)\}\); 输出: 加法模型 \(f(x)\) 。

1. 初始化 \(f_0(x)=0\);
2. 对 \(m=1,2, \cdots, M\)

1. 极小化损失函数

\[ \left(\beta_m, \gamma_m\right)=\arg \min_{\beta, \gamma} \sum_{i=1}^N L\left(y_i, f_{m-1}\left(x_i\right)+\beta b\left(x_i ; \gamma\right)\right) \]

得到参数 \(\beta_m, \gamma_m\) 。

2. 更新

\[ f_m(x)=f_{m-1}(x)+\beta_m b\left(x ; \gamma_m\right) \]

3. 得到加法模型

\[ f(x)=f_M(x)=\sum_{m=1}^M \beta_m b\left(x ; \gamma_m\right) \]

学过GBDT的话就感觉会很熟悉。实际上提升树和GBDT也都是使用的前向分步算法。 直接上结论吧，推导的感觉没有必要，毕竟都是boosting方法。具体证明的过程可以看李航老师的《统计学习方法》。

Adaboost算法是前向分步加法算法的特例，这时，模型是由基本分类器组成的加法模型，损失函数是指数函数。

总结

总是要写个总结的，adaboost一种boosting方法，就是不断迭代调整权重，最后将每一步的结果加权求和，可以说是一种典型的boosting的方法。