Activation checkpointing
为什么存储激活值?
首先回顾为什么要存储激活值。 简单来说,模型参数是根据导数更新的。为了有效地计算这些导数,必须缓存某些张量。激活内存是这些缓存张量的内存成本。 具体来说,以 \(f\) 是矩阵乘法运算:
\[y=f(x)=W\cdot x\] \(W\)是一个可学习的权重矩阵。假设我们有关于 早期反向传播阶段的手头输出,\(\frac{\partial L}{\partial y}\),我们 需要计算 两个额外的梯度: 1.关于\(W\),以便我们可以更新此权重。 2.关于\(x\),这样我们就可以继续反向传播算法 到产生的任何作\(x\)
前导数是
\[\frac{\partial L}{\partial W}=\frac{\partial L}{\partial y}\frac{\partial y}{\partial W}=\frac{\partial L}{\partial y}\times x\]
而后者的导数是
\[\frac{\partial L}{\partial x}=\frac{\partial L}{\partial y}\cdot W\]
因此,如下图所示,我们需要缓存输入张量 \(x\) 为了能够计算我们关心的导数。节省的成本
\(x\) 是激活 memory。 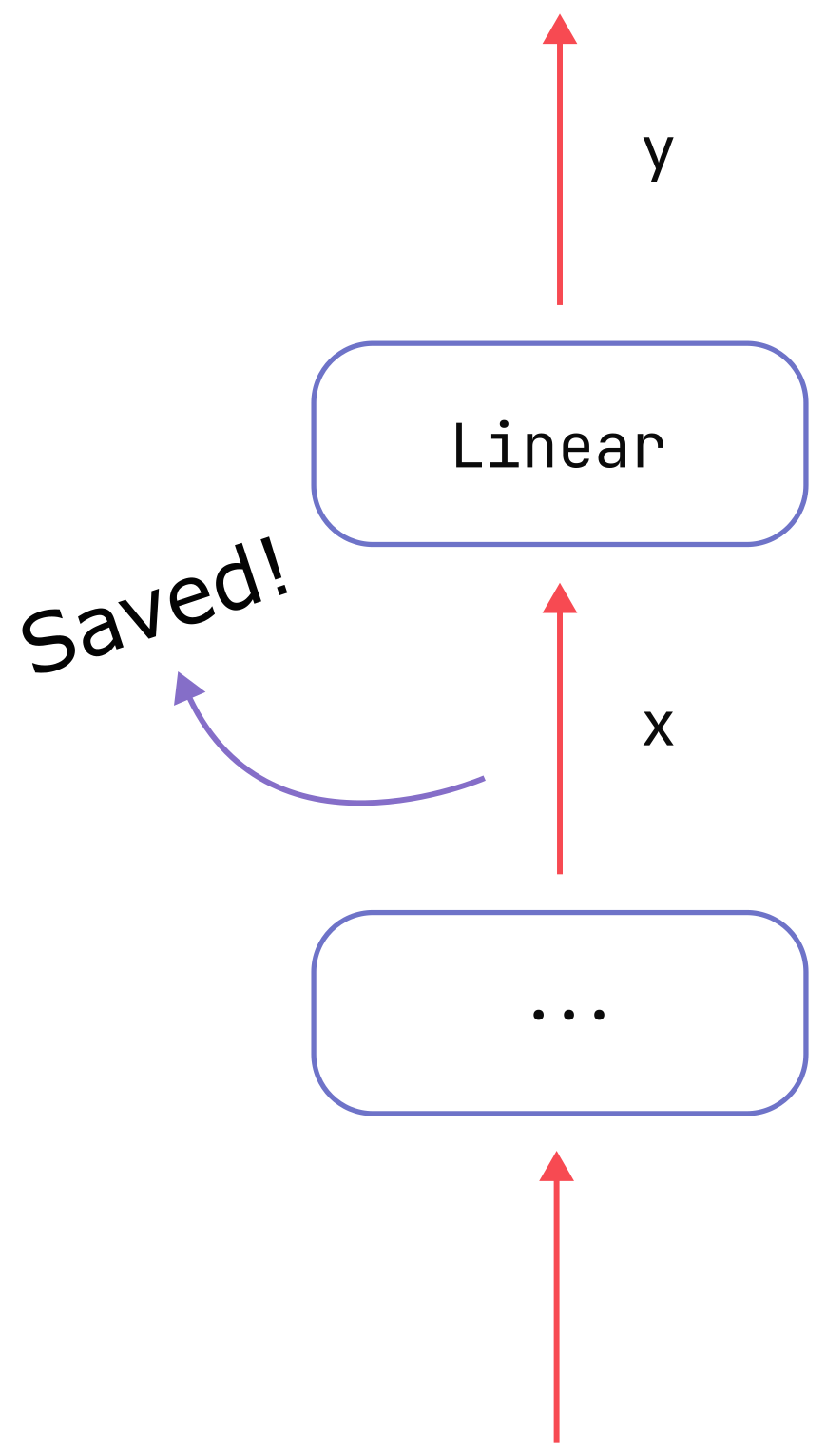
我们发现只需要保存 x,而对于 y 不需要保存,也就是说我们只保存反向传播时绝对需要的激活值,其它的临时变量要立即释放。
MLP
class MLP(nn.Module):
"""
Basic MLP (multi-layer perceptron) layer with optional Dropout.
"""
def __init__(
self,
d_model: int,
act_fn: nn.Module,
dropout_prob: Optional[float] = None,
device: Optional[Union[str, torch.device]] = None,
dtype: Optional[torch.dtype] = None,
) -> None:
super().__init__()
self.d_model = d_model
self.act_fn = act_fn
self.dropout_prob = dropout_prob
factory_kwargs = {"device": device, "dtype": dtype}
self.lin_0 = nn.Linear(self.d_model, 4 * self.d_model, **factory_kwargs)
self.lin_1 = nn.Linear(4 * self.d_model, self.d_model, **factory_kwargs)
self.dropout = nn.Dropout(self.dropout_prob) if self.dropout_prob else None
def forward(self, inputs: torch.Tensor) -> torch.Tensor:
x = self.lin_0(inputs)
x = self.act_fn(x)
x = self.lin_1(x)
if self.dropout is not None:
x = self.dropout(x)
return x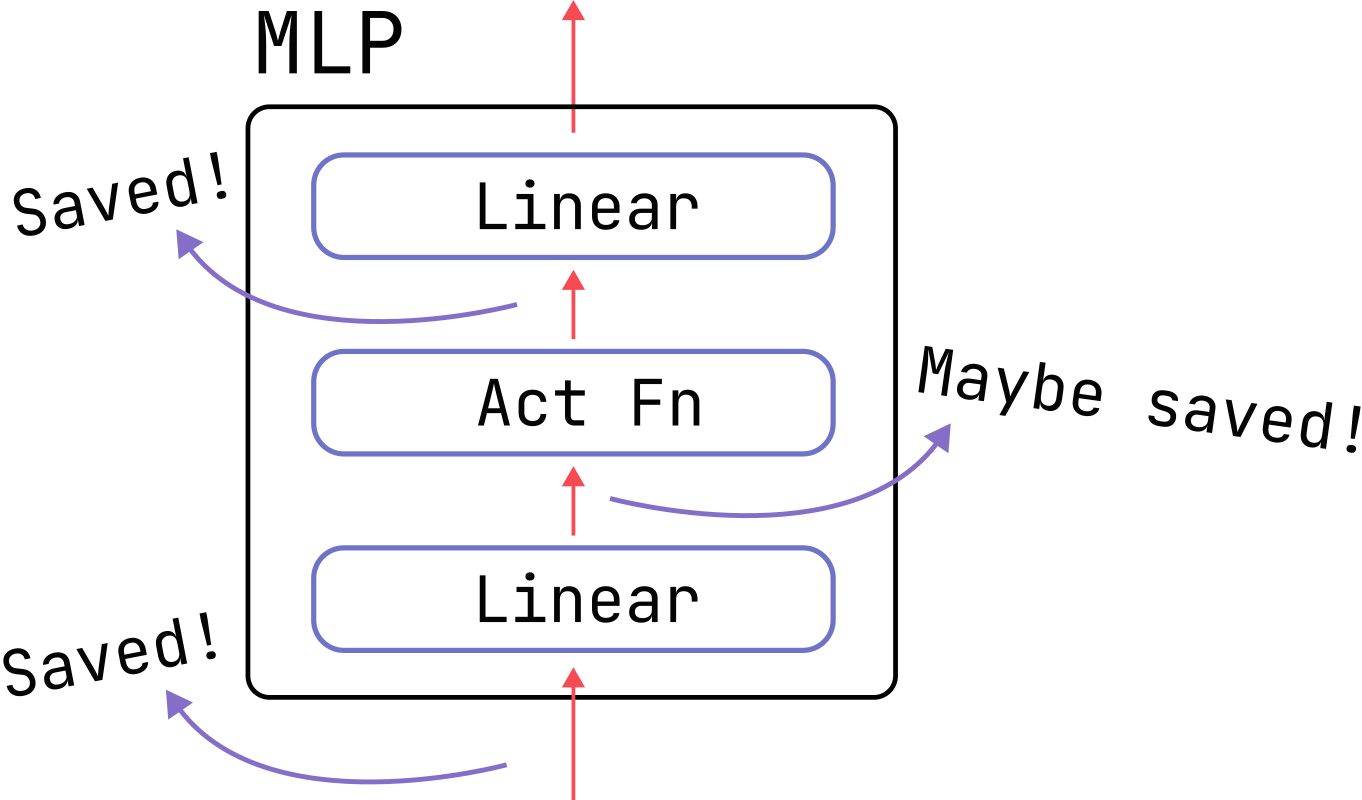
Maybe saved 的是否 是根据激活函数的类型来的: 如果是 GELU 激活函数
\[y=\frac x2\times\tanh\left(\sqrt{\frac2\pi}\left(x+.044715x^3\right)\right)\] 这时候计算梯度的话还是需要输入 x,这是需要存储的情况
而如果是一些特殊的激活函数的话,比如 ReLU
\[y=\mathsf{ReLU}(x)=\begin{cases}x&\mathrm{if~}x>0\\0&\mathrm{if~}x<0&\end{cases}\]
梯度为:
\[\frac{dy}{dx}=\frac{d\text{ ReLU}(x)}{dx}=\begin{cases}1&\mathrm{if~}x>0\\0&\mathrm{if~}x<0&\end{cases}\]
就不需要存储。 Tanh 也是同理:
\[ \frac{dy}{dx} = \frac{d\tanh (x)}{dx} = 1-\tanh(x)^2 = 1-y^2 \]
如果想要性能,选择 GELU,想要低显存,使用 ReLU。
激活值计算
根据博客 # 分析transformer模型的参数量、计算量、中间激活、KV cache 内容来得到激活值的计算公式。
大模型在训练过程中通常采用混合精度训练,中间激活值一般是float16或者bfloat16数据类型的。在分析中间激活的显存占用时,假设中间激活值是以float16或bfloat16数据格式来保存的,每个元素占了2个bytes。唯一例外的是,dropout操作的mask矩阵,每个元素只占1个bytes。在下面的分析中,单位是bytes,而不是元素个数。
先分析 self-attention 块的中间激活。Self-attention 块的计算公式如下: \[Q=xW_Q,K=xW_K,V=xW_V\]
\[x_{out}=softmax(\frac{QK^T}{\sqrt{h}})\cdot V\cdot W_o+x\]
- 对于 \(Q,K,V\) ,需要保存它们共同的输入 \(x\) ,这就是中间激活。输入 \(x\) 的形状为 \([b,s,h]\) ,元素个数为 bsh ,占用显存大小为 \(2*bsh=2bsh\) 。
- 对于 \(QK^T\) 矩阵乘法,需要保存中间激活 \(Q,K\) ,两个张量的形状都是 \([b,s,h]\) ,占用显 存大小合计为 \(2*2*bsh=4bsh\) 。
- 对于 \(softmax()\) 函数,需要保存函数的输入 \(QK^T\) ,占用显存大小为 \(2bs^2a\) ,这里的 \(a\) 表示注意力头数。
\[score=softmax(\frac{QK^T}{\sqrt{d_k}})\]
\(Q\) 的形状为:\([ b, head\_ num, s, per\_ head\_ hidden\_ size]\) \(K^T\) 的形状为:\([b,head\_num,per\_head\_hidden\_size,s]\) \(QK^T\) 的形状为:\([b,head\_num,s,s]\) ,元素个数为 \(bs^2a\) ,占用显存大小为 \(2bs^2a\) 。 4. 计算完 \(softmax()\) 函数后,会进行 dropout 操作。需要保存一个 mask 矩阵,mask 矩阵的形状与 \(QK^T\) 相同,占用显存大小为 \(bs^2a\) 。 5. 计算在 \(V\) 上的 attention,即 \(score\cdot V\), 需要保存 score ,大小为 \(2bs^2a\) ;以及 \(V\) ,大小为 \(2bsh\) 。二者占用显存大小合计为 \(2bs^2a+2bsh\) 。 6. 计算输出映射以及一个 dropout 操作。输入映射需要保存其输入,大小为 \(2bsh\) ;dropout 需要保存 mask 矩阵,大小为 bsh 。二者占用显存大小合计为 \(3bsh\) 。 因此,将上述中间激活相加得到,self-attention 块的中间激活占用显存大小为 \(11bsh+5bs^2a\) 。
接下来看 MLP 块的中间激活。MLP 块的计算公式如下:
\[x=f_{gelu}(x_{out}W_1)W_2+x_{out}\]
- 第一个线性层需要保存其输入,占用显存大小为 \(2bsh\) 。
- 激活函数需要保存其输入,占用显存大小为 \(8bsh\) 。
- 第二个线性层需要保存其输入,占用显存大小为 \(8bsh\) 。
- 最后有一个 dropout 操作,需要保存 mask 矩阵,占用显存大小为 bsh 。 对于 MLP 块,需要保存的中间激活值为 19 bsh 。 另外,self-attention 块和 MLP 块分别对应了一个 layer normalization。每个 layer norm 需要保存其输入,大小为 \(2bsh\) (忽略了均值和方差的2 bs,如果不忽略应当为 2 bsh+4 bs,这里的单位都是 bytes)。2 个 layer norm 需要保存的中间激活为 \(4bsh\) 。 综上,每个 transformer 层需要保存的中间激活占用显存大小为 \(34bsh+5bs^2a\)。对于 \(l\) 层 transformer 模型,还有 embedding 层、最后的输出层。Embedding 层不需要中间激活。总的而言,当隐藏维度 \(h\) 比较大,层数 \(l\) 较深时,这部分的中间激活是很少的,可以忽略。因 此,对于 \(l\) 层 transformer 模型,中间激活占用的显存大小可以近似为 \((34bsh+5bs^2a)*l\)
Activation checkpointing
当使用该方法时,我们只需要保存一些关键的激活值,可以舍弃一些激活值从而在反向传播的过程中重新计算,通常有两种策略:
Full:我们在 Transformer 模型每一层之间的过渡点检查激活值。这通常被称为“完整”策略,因为它需要每层都进行一次前向传播,即在反向传播过程中增加了一次完整的前向传播。这种策略节省的内存最多,但在计算方面成本最高。它通常会使计算成本和时间增加高达 30-40%,这一影响非常显著。
Select:总体而言,我们可以比全面优化做得更好。那篇关于重新计算的论文的作者进行了详细分析,研究了哪些激活值的增长最大,并且以每秒浮点运算次数(FLOPS)为标准,其重新计算成本最低。结果表明,注意力计算属于这一类别,因此我们通常可以丢弃它们,而专注于对昂贵的前馈计算进行检查点设置。对于 GPT-3(1750 亿参数)模型而言,这意味着在计算成本仅增加 2.7%的情况下,激活值内存减少了 70%。
如今,大多数训练框架都使用 FlashAttention,它通过在反向传播中重新计算注意力得分和矩阵,而不是存储它们,将激活重新计算集成到其优化策略中。因此,大多数使用 FlashAttention 的人已经在使用 AC。 由于重新计算,激活重新计算略微增加了 FLOPS 的数量,同时显著降低了内存访问开销。 这种权衡在 GPU 等高速内存有限的硬件上特别有利,因为访问内存通常比执行计算慢。尽管涉及额外的操作,但总体效果通常是计算速度更快,内存占用更少。
1. Full Activation Checkpointing (全量激活值检查点)
这是最经典、最直接的检查点方法。
工作原理:
- 分段: 将整个模型的计算图(所有层)在逻辑上划分为若干个段 (Segment)。
- 保存: 在前向传播时,只保存每个段的输入张量 (Input Tensor)。这些被保存的张量就是“检查点”。段内所有中间层的激活值都会在计算后被立即丢弃,不占用显存。
- 重算: 在反向传播时,当需要某个段内的激活值来计算梯度时,它会找到该段的检查点(即该段的输入),然后重新执行该段的前向传播,以恢复所需要的激活值。一旦这个激活值被使用完毕,它会再次被丢弃。
图解:
假设一个模型有16层,我们每4层设置一个检查点:
标准训练 (无Checkpointing):
[Input] -> L1 -> L2 -> ... -> L16 -> [Output]
- 前向传播: 计算并存储 L1 到 L16 的所有激活值。 -
内存占用: 极高。
Full Activation Checkpointing:
[Input] -> [Segment 1: L1-L4] -> [Segment 2: L5-L8] -> [Segment 3: L9-L12] -> [Segment 4: L13-L16] -> [Output]
- 前向传播: - 执行 Segment 1 (L1-L4),只保存 L5
的输入(即L4的输出)作为检查点,丢弃 L1-L3 的激活值。 - 执行
Segment 2 (L5-L8),只保存 L9 的输入作为检查点,丢弃
L5-L7 的激活值。 - …以此类推。 - 反向传播: - 当需要计算
L12 的梯度时,发现它的激活值没有被保存。 -
系统加载最近的检查点(L9的输入)。 - 重新计算 L9 ->
L10 -> L11 -> L12 的前向传播,得到 L12 的激活值。 -
使用该激活值计算梯度,然后丢弃它。
优缺点:
- 优点:
- 效果显著: 可以大幅度降低显存占用,内存占用量与模型的层数基本无关,只与最长的那个段的计算复杂度有关。
- 实现简单: 逻辑清晰,易于在各种框架中实现(例如
PyTorch 的
torch.utils.checkpoint)。
- 缺点:
- 计算开销大: 每个被 checkpoint 的段(除了最后一个)都会被重新计算一次。如果模型很大,这会带来大约 30%-50% 甚至更高的训练时间开销。
2. Selective Activation Checkpointing (选择性激活值检查点)
这是对全量检查点方法的智能化升级,也是目前更受关注的重点。它认识到“全量丢弃、全量重算”的策略过于粗暴和低效。
核心思想:
在同一个计算段内,不同的操作(Op)或激活值,其存储成本和重算成本是不同的。
- 有些激活值占用显存大,但重算很快(例如 ReLU, Dropout 等元素级操作)。
- 有些激活值占用显存小,但重算很慢(例如 MatMul, Convolution 的输出)。
Selective Checkpointing 的目标就是:在每个段内,不再丢弃所有激活值,而是有选择性地保存那些“重算成本高、存储成本低”的激活值,从而在反向传播时,避免代价高昂的重计算。
工作原理:
- 成本分析: 它需要对计算图中的每个操作进行成本分析。
- 存储成本: 该操作输出的激活值张量占用的显存大小。
- 重算成本: 重新计算出这个激活值所需要的时间(通常用 FLOPs 衡量)。
- 智能决策:
基于成本分析,算法(通常是动态规划或启发式搜索)会做出决策。对于段内的每一个激活值,它会判断:
- 是直接保存它更划算?
- 还是丢弃它,之后再通过重计算恢复更划算?
- 选择性保存与重算:
- 在前向传播时,除了保存每个段的输入(主检查点)外,还会额外保存段内那些被判定为“值得保存”的少量关键激活值。
- 在反向传播时,当需要一个激活值时,如果它被保存了,就直接使用。如果没被保存,系统会从最近的一个检查点(无论是主检查点还是段内保存的次级检查点)开始重算,而不是必须从段的开头开始。
图解(续上例):
在 Segment 3 (L9-L12) 中:
L9 (MatMul) -> L10 (LayerNorm) -> L11 (ReLU) -> L12 (MatMul)
- Full Checkpointing 会丢弃 L9, L10, L11 的所有输出。重算 L12 时需要从 L9 的输入开始,重新执行 MatMul, LayerNorm, ReLU。
- Selective Checkpointing 可能会做出如下决策:
- L9 (MatMul) 的输出:重算成本极高,但存储成本可能相对可控。决策:保存。
- L11 (ReLU) 的输出:占用显存和 L10 一样大,但重算成本极低(只需对 L10 的输出再做一次 ReLU)。决策:丢弃。
在反向传播时: - 当需要 L11 的激活值时,发现它没被保存。但系统发现
L10 的激活值(或者 L9 的)被保存了。 - 它只需从 L10 开始重算
L10 -> L11 (ReLU),而无需重算昂贵的
L9 (MatMul)。
优缺点:
- 优点:
- 最佳平衡: 在实现与 Full Checkpointing 几乎相同显存节省效果的同时,显著降低了重计算的开销,从而缩短了训练时间。它在“时间”和“空间”之间找到了一个更优的平衡点。
- 高效: 相比 Full Checkpointing,训练速度更快。
- 缺点:
- 实现复杂: 需要对模型的计算图进行深入分析,并建立准确的成本模型。这通常需要深度学习框架或特定库(如 DeepSpeed)的底层支持。
- 模型依赖: 优化的效果依赖于模型结构。对于包含大量昂贵操作的模型,效果会更明显。
总结对比
| 特性 | Full Activation Checkpointing | Selective Activation Checkpointing |
|---|---|---|
| 核心策略 | 以时间换空间 | 在时间和空间之间寻找最优平衡 |
| 粒度 | 粗粒度 (段级别) | 细粒度 (操作级别) |
| 保存内容 | 仅保存每个段的输入 | 保存每个段的输入 + 段内部分关键激活值 |
| 重算方式 | 总是从段的开头重算整个段 | 从最近的可用检查点开始重算,路径更短 |
| 计算开销 | 高 | 较低 |
| 显存节省 | 非常高 | 非常高 (与 Full 类似) |
| 实现复杂度 | 低 | 高 |
总而言之,Selective Activation Checkpointing 是对传统检查点技术的一次重大优化。它通过更精细化的资源管理,在不牺牲太多内存节省的前提下,大幅减少了因重计算带来的时间惩罚,是目前训练超大规模模型时更为先进和高效的主流技术之一。 ## 参考 Activation Memory: A Deep Dive using PyTorch | Determined AI