线性回归
参考:https://cuijiahua.com/blog/2017/11/ml_11_regression_1.html
什么是回归?
回归的目的是预测数值型的目标值。最直接的办法是依据输入写出一个目标值的计算公式。
HorsePower = 0.0015 * annualSalary - 0.99 * hoursListeningToPublicRadio
这就是所谓的回归方程(regression equation),其中的0.0015和-0.99称为回归系数(regression weights),求这些回归系数的过程就是回归。一旦有了这些回归系数,再给定输入,做预测就非常容易了。具体的做法是用回归系数乘以输入值,再将结果全部加在一起,就得到了预测值。
说到回归,一般都是指线性回归(linear regression),所以本文里的回归和线性回归代表同一个意思。线性回归意味着可以将输入项分别乘以一些常量,再将结果加起来得到输出。
这里的线性可以是对变量的线性,也可以是对参数的线性。比如\(y=x^2\)可以认为是一个线性函数。
正规方程推导
将向量表达形式转为矩阵表达形式,则有 \(J(\theta)=\frac{1}{2}(X \theta-y)^{2}\) ,其中 \(X\) 为 \(m\) 行 \(n\) 列的矩阵( \(m\) 为样本个数, \(n\) 为特 征个数), \(\theta\) 为 \(n\) 行1列的矩阵, \(y\) 为 \(m\) 行1列的矩阵,对 \(J(\theta)\) 进行如下变换
\[ \begin{aligned} &J(\theta)=\frac{1}{2}(X \theta-y)^{T}(X \theta-y) \\\\ &=\frac{1}{2}\left(\theta^{T} X^{T}-y^{T}\right)(X \theta-y) \\\\ &=\frac{1}{2}\left(\theta^{T} X^{T} X \theta-\theta^{T} X^{T} y-y^{T} X \theta-y^{T} y\right) \end{aligned} \]
接下来对 \(J(\theta)\) 偏导,需要用到以下几个矩阵的求导法则:
\[ \begin{aligned} &\frac{d A B}{d B}=A^{T} \\\\ &\frac{d X^{T} A X}{d X}=2 A X \end{aligned} \]
所以有:
\[ \begin{aligned} &\frac{\partial J(\theta)}{\partial \theta}=\frac{1}{2}\left(2 X^{T} X \theta-X^{T} y-\left(y^{T} X\right)^{T}-0\right) \\\\ &=\frac{1}{2}\left(2 X^{T} X \theta-X^{T} y-X^{T} y-0\right) \\\\ &=X^{T} X \theta-X^{T} y \\\\ &\text { 令 } \frac{\partial J(\theta)}{\partial \theta}=0 } \\\\ {\text { 则有 } \theta=\left(X^{T} X\right)^{-1} X^{T} y} \end{aligned} \]

值得注意的是,上述公式中包含逆矩阵,也就是说,这个方程只在逆矩阵存在的时候使用,也即是这个矩阵是一个方阵,并且其行列式不为0。
除了这种方法,也可以使用最小二乘法来解决。
局部加权线性回归
线性回归的一个问题是有可能出现欠拟合现象,因为它求的是具有小均方误差的无偏估 计。显而易见,如果模型欠拟合将不能取得好的预测效果。所以有些方法允许在估计中引入一 些偏差,从而降低预测的均方误差。
其中的一个方法是局部加权线性回归(Locally Weighted Linear Regression,LWLR)。 普通线性回归:
\[ \min J_R=\sum_{i=1}^m\left(g\left(x_i\right)-y_i\right)^2 \]
局部加权线性回归:
\[ \min J_{L R}=\sum_{i=1}^m \theta_i\left(g\left(x_i\right)-y_i\right)^2 \]
这里唯一的区别是加入了权重 \(\theta\), 采用之前的最小二乘法求解权数 \(\mathbf{w}\) :
\[ \hat{\mathbf{w}}^* =\arg \min_{\hat{\mathbf{w}}} \theta(\mathbf{y}-\mathbf{X} \hat{\mathbf{w}})^T(\mathbf{y}-\mathbf{X} \hat{\mathbf{w}}) \]
在该方法中,我们给待预测点附近的每个点赋予一定的权重。与kNN一样,这种算法每次预测均需要事先选取出对应的数据子集。该算法解除回归系数W的形式如下:
\[ \hat{w} = (X^T\theta X)^{-1}X^T\theta y \]
其中W是一个矩阵,这个公式跟我们上面推导的公式的区别就在于W,它用来给每个店赋予权重。
LWLR使用”核”(与支持向量机中的核类似)来对附近的点赋予更高的权重。核的类型可以自由选择,最常用的核就是高斯核,高斯核对应的权重如下:
\[ \theta(i,i) = exp\left ( \frac{ (x^{(i)}-x)^2}{-2k^2}\right) \]
这样就构造了一个只含对角元素的权重矩阵 \(w\) ,并且点xi与 \(x\) 越接近, \(\theta(i, i)\) 的值越大,当 \(x i\) 与 \(x\) 非常接近时, \(\theta(i, i)\) 的值趋于 1 ,我们再回头看之前的优化式:
\[ \min J_{L R}=\sum_{i=1}^m \theta_i\left(g\left(x_i\right)-y_i\right)^2 \]
对于一个数据点,与其靠近的点,权重大,与其相距较远的点,权重小,从而优化问题会有所偏倚,靠近的点对该数据点的回归拟合起较大作用,而相距较远的 点由于权数很小,造成的影响基本可以忽略不计,这样就等同于每个点的回归都是基于与其相距较近的点为基础,而忽略了较远的点,这也就是同部加权线性回归局部的由来,因为它着重考虑目标点同部的数据点为回归基础.
可以看到,加权函数只有一个系数,那就是分母上的 \(k\) ,当K取很小时, exp得到的很多值均趋于 0 ,此时只有很少一部分样本用于训练,而当k取很大时, exp的值 不会很快趋于 0 ,从而会有一大部分点用于训练,我们可以通过调整k的值,决定这个‘局部’的大小究竟是多大
如果数据的特征比样本点还多应该怎么办?如果矩阵有多重共线性怎么办?很显然,此时我们不能再使用上文的方法进行计算了,因为矩阵X不是满秩矩阵,非满秩矩阵在求逆时会出现问题。
解决的方法就是正则化。在线性回归中,正则化主要有L1正则化与L2正则化,L1正则化对应LASSO回归,L2正则化对应岭回归。
#!/usr/bin/env python
#-*- coding:utf-8 -*-
from numpy import *
import matplotlib.pyplot as plt
"""
打开一个用tab键分隔的文本文件
parameters:
fileName -文件名
return:
dataMat -数据矩阵
labelMat -目标值向量
"""
def loadDataSet(fileName):
numFeat = len(open(fileName).readline().split('\t')) - 1 #得到列数,不包括最后一列,默认最后一列值为目标值
dataMat = []; labelMat = []
fr = open(fileName)
for line in fr.readlines():
lineArr =[]
curLine = line.strip().split('\t')
for i in range(numFeat):
lineArr.append(float(curLine[i]))
dataMat.append(lineArr)
labelMat.append(float(curLine[-1]))
return dataMat,labelMat
"""
计算最佳拟合直线
parameters:
xArr -给定的输入值
yArr -给定的输出值
return:
ws -回归系数
"""
def standRegres(xArr,yArr):
xMat = mat(xArr); yMat = mat(yArr).T #将数据保存到矩阵中
#计算x.T *x
xTx = xMat.T @ xMat
#使用linalg.det()方法来判断它的行列式是否为零,即是否可逆
if linalg.det(xTx) == 0.0:
return
#使用最小二乘法计算w值
ws = linalg.inv(xTx) @ xMat.T @ yMat
return ws
"""
计算局部加权线性回归系数
parameters:
testPoint -待预测数据
xArr -给定输入值
yArr -给定输出值
k -高斯核的k值,决定对附近的点赋予多大的权重
return:
testPoint * ws -回归预测的估计值
"""
def lwlr(testPoint, xArr, yArr, k=1.0):
xMat = mat(xArr); yMat = mat(yArr).T #读入数据到矩阵
m = shape(xMat)[0]
#创建对角权重矩阵,该矩阵为方阵,矩阵维数为样本点个数
theta = eye(m, m)
#遍历整个数据集
for i, x in enumerate(xMat):
#计算待预测数据与每个样本点的差值
x_i = (testPoint - x) @ (testPoint - x).T
#计算每个样本点对应的权重值,随着样本点与待预测点距离的递增,权重将以指数级衰减
theta[i][i] = exp(x_i / (-2 * k ** 2))
#计算x.T θ x
xT_theta_x = xMat.T @ theta @ xMat
#判断矩阵是否可逆
if linalg.det(xT_theta_x) == 0:
return
#使用最小二乘法计算w值
ws = linalg.inv(xT_theta_x) @ (xMat.T @ (theta @ yMat))
return testPoint*ws
"""
测试函数
parameters:
testArr -测试数据集
xArr -给定输入值
yArr -给定输出值
k -高斯核的k值
return:
yHat -预测值
"""
def lwlrTest(testArr, xArr, yArr,k=1.0):
m = shape(xArr)[0]
yHat = zeros(m)
for i in range(m):
yHat[i] = lwlr(testArr[i],xArr,yArr,k)
return yHat
"""
计算预测误差的平方和
parameters:
yArr -给定y值
yHatArr -预测y值
return:
((yArr-yHatArr)**2).sum() -误差矩阵
"""
def rssError(yArr,yHatArr):
return ((yArr-yHatArr)**2).sum()
if __name__=='__main__':
abX,abY = loadDataSet('linear_regression_abalone/abalone.txt')
yHat01 = lwlrTest(abX[0:99],abX[0:99],abY[0:99],0.1)
yHat1 = lwlrTest(abX[0:99],abX[0:99],abY[0:99],1)
yHat10 = lwlrTest(abX[0:99],abX[0:99],abY[0:99],10)
print("使用局部加权线性回归预测误差:")
print("核为0.1时:",rssError(abY[0:99],yHat01.T))
print("核为1时:",rssError(abY[0:99],yHat1.T))
print("核为10时:",rssError(abY[0:99],yHat10.T))
yHat01 = lwlrTest(abX[100:199],abX[0:99],abY[0:99],0.1)
yHat1 = lwlrTest(abX[100:199],abX[0:99],abY[0:99],1)
yHat10 = lwlrTest(abX[100:199],abX[0:99],abY[0:99],10)
print("使用局部加权线性回归预测误差在新数据上的表现:")
print("核为0.1时:",rssError(abY[100:199],yHat01.T))
print("核为1时:",rssError(abY[100:199],yHat1.T))
print("核为10时:",rssError(abY[100:199],yHat10.T))
ws = standRegres(abX[0:99],abY[0:99])
yHat = mat(abX[100:199])*ws
print("使用标准线性回归预测误差为:",rssError(abY[100:199],yHat.T.A))岭回归
岭回归即我们所说的L2正则线性回归,在一般的线性回归最小化均方误差的基础上增加了一个参数w的L2范数的罚项,从而最小化罚项残差平方和:
\[ min\mid \mid Xw-y \mid\mid_2^2 + \lambda \mid\mid w\mid\mid_2^2 \] 简单说来,岭回归就是在普通线性回归的基础上引入单位矩阵。回归系数的计算公式变形如下:
\[ \hat{w} = (X^TX+\lambda I)^{-1}X^Ty \] 式中,矩阵I是一个mxm的单位矩阵,加上一个λI从而使得矩阵非奇异,进而能对矩阵求逆。
当\(\lambda\)过小,则相当于原来的正规方程,会造成过拟合,而\(\lambda\)过大时,模型的方差会更小,但偏差会变大,所以岭回归的关键是找到一个合理的\(\lambda\)值来平衡模型的方差和偏差。
岭回归最先用来处理特征数多于样本数的情况,现在也用于在估计中加入偏差,从而得到更好的估计。这里通过引入λ来限制了所有w之和,通过引入该惩罚项,能够减少不重要的参数,这个技术在统计学中也可以叫做缩减(shrinkage)。
缩减方法可以去掉不重要的参数,因此能更好地裂解数据。此外,与简单的线性回归相比,缩减法能够取得更好的预测效果。
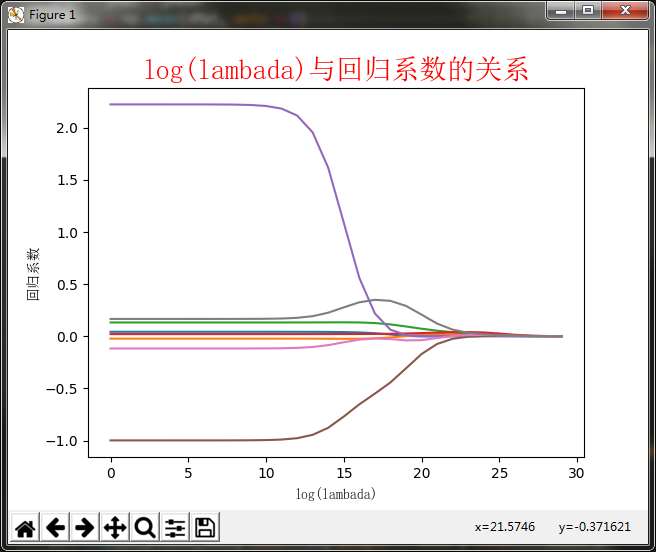
图绘制了回归系数与log(λ)的关系。在最左边,即λ最小时,可以得到所有系数的原始值(与线性回归一致);而在右边,系数全部缩减成0;在中间部分的某个位置,将会得到最好的预测结果。想要得到最佳的λ参数,可以使用交叉验证的方式获得,文章的后面会继续讲解。
Lasso
Lasso对回归系数做了限定,对应的约束条件如下:
\[ \sum_{k=1}^n|w_k| \leq \lambda \]
而岭回归的约束条件如下:
\[ \sum_{k=1}^nw_k^2 \leq \lambda \]
唯一不同点在于,Lasso的约束条件用绝对值取代了平方和,虽然约束形式稍作变化,但结果大相径庭,细微的变化极大地增加了计算复杂度。所以用更简单的前向逐步回归来取代。
前向逐步回归
前向逐步线性回归算法属于一种贪心算法,即每一步都尽可能减少误差。我们计算回归系数,不再是通过公式计算,而是通过每次微调各个回归系数,然后计算预测误差。那个使误差最小的一组回归系数,就是我们需要的最佳回归系数。
该算法的伪代码如下:
数据标准化,使其满足0均值和单位方差。
- 在每轮迭代中:
- 设置当前最小误差lowestError为正无穷
- 对每个特征
- 增大或缩小
- 改变一个系数得到新的W
- 计算新W下的误差
- 如果误差Error小于当前最小误差lowestError:设置Wbest等于当前的W
- 将W设置为新的Wbest
- 增大或缩小
代码
使用的优化算法是梯度下降法,还有一个随机梯度下降
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(42)
w = np.array([2, 1, 4, 5, 3])
d = len(w)
X = []
Y = []
for _ in range(1000000):
x = np.random.randn(d)
y = w.dot(x) + np.random.randn()
X.append(x)
Y.append(y)
X = np.array(X)
Y = np.array(Y)
def mse(y_true, y_test):
return ((y_true - y_test) ** 2) / len(y_true)
def gradient(y_true, y_test):
return 2 * (y_test - y_true) / len(y_true)
def batch_gradient_descent(w, alpha, x, y):
y_pred = x.dot(w)
error = mse(y, y_pred).mean()
grad = np.dot(x.T, gradient(y, y_pred))
w = w - alpha * grad
return w, error
def stochastic_gradient_descent(w, alpha, x, y, epoch):
alpha_update = alpha
for i in range(len(x)):
y_pred = x[i].dot(w)
grad = np.dot(x[i].T, (y_pred - y[i])) * 2 / len(x)
w = w- alpha_update * grad
alpha_update = alpha_update / (epoch+1)
error = mse(y, x.dot(w)).mean()
return w, error
X_test = []
Y_test = []
for _ in range(10000):
x = np.random.randn(d)
y = w.dot(x) + np.random.randn()
X_test.append(x)
Y_test.append(y)
X_test = np.array(X_test)
Y_test = np.array(Y_test)
def l2_mse(y_true, y_test, l, w):
return ((y_true - y_test) ** 2) / len(y_true) + l * np.sum(w ** 2)
def l2_gradient(y_true, y_test):
return 2 * (y_test - y_true) / len(y_true)
def batch_gradient_descent_with_l2(w, alpha, x, y, l):
y_pred = x.dot(w)
error = l2_mse(y, y_pred, l, w).mean()
grad = np.dot(x.T, l2_gradient(y, y_pred))
w = w - alpha * grad - alpha * l * w *2
return w, error
if __name__ == "__main__":
train_loss = []
test_loss = []
print("Batch Gradient Descent")
for epoch in range(1000):
w, error = batch_gradient_descent(w, 0.01, X, Y) # train
y_pred = X_test.dot(w)
error_test = mse(Y_test, y_pred).mean() # test
if epoch % 100 == 0:
print("Epoch: {}, TrainError: {}, TestError: {}".format(epoch, error, error_test))
train_loss.append(error)
test_loss.append(error_test)
plt.plot(train_loss, label="Train-No-L2")
plt.legend()
plt.xlabel("Epoch")
plt.ylabel("Loss")
plt.show()
plt.plot(test_loss, label="Test-No-L2")
plt.xlabel("Epoch")
plt.ylabel("Loss")
plt.legend()
plt.show()
plt.plot(train_loss, label="Train-No-L2")
plt.plot(test_loss, label="Test-No-L2")
plt.legend()
plt.show()
# ============================================
train_loss = []
test_loss = []
print("Batch Gradient Descent with L2")
l = 0.0001 # lambda
for epoch in range(1000):
w, error = batch_gradient_descent_with_l2(w, 0.01, X, Y, l) # train
y_pred = X_test.dot(w)
error_test = l2_mse(Y_test, y_pred, l, w).mean() # test
if epoch % 100 == 0:
print("Epoch: {}, TrainError: {}, TestError: {}".format(epoch, error, error_test))
train_loss.append(error)
test_loss.append(error_test)
plt.plot(train_loss, label="Train-L2")
plt.legend()
plt.xlabel("Epoch")
plt.ylabel("Loss")
plt.show()
plt.plot(test_loss, label="Test-L2")
plt.xlabel("Epoch")
plt.ylabel("Loss")
plt.legend()
plt.show()
plt.plot(train_loss, label="Train-L2")
plt.plot(test_loss, label="Test-L2")
plt.legend()
plt.show()其实很简单,就是数学公式的复现。 ## 总结
缩减方法(逐步线性回归或岭回归),就是将一些系数缩减成很小的值或者直接缩减为0。这样做,就增大了模型的偏差(减少了一些特征的权重),通过把一些特征的回归系数缩减到0,同时也就减少了模型的复杂度。消除了多余的特征之后,模型更容易理解,同时也降低了预测误差。