温度超参数t，一般为softmax结果除以该参数，或者在对比学习中，相似度除以参数t。 如图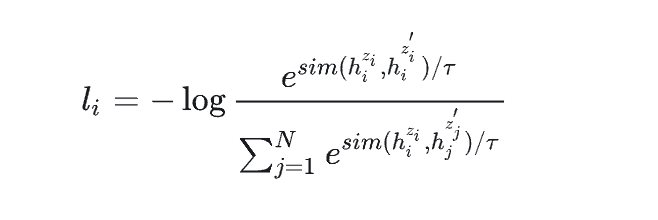： 上图为无监督simcse中的损失函数。

t越大，结果越平滑，t越小，得到的概率分布更“尖锐”。 当t趋于0时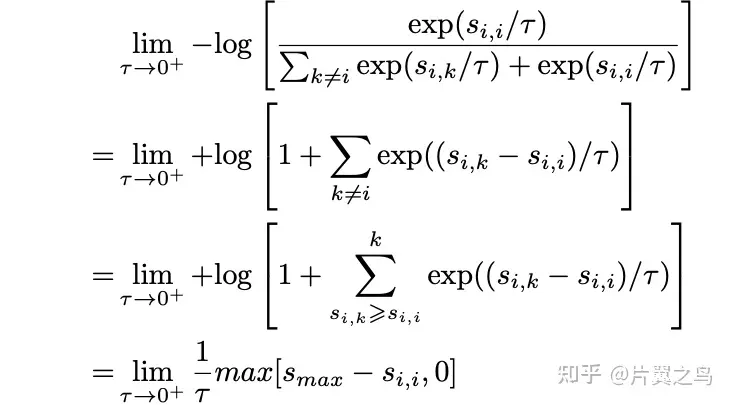： 此时只关注最困难的负样本（smax）。 当t趋于∞时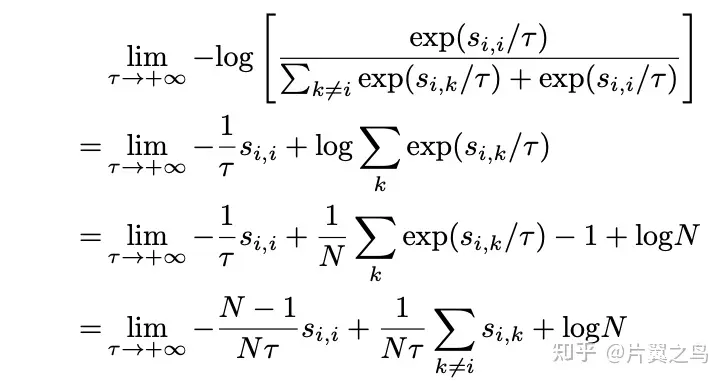： 此时对比损失对所有负样本的权重都相同。

因此t越大，可以避免陷入局部最优解。(局部最优是过早地确定了优化的梯度方向，失去了在其他方向上探索的机会。较大的温度使得各个方向上的梯度差异没有那么明显，从而获得了在早期更多的探索机会。)

[!note] 温度系数的作用是调节对困难样本的关注程度：越小的温度系数越关注于将本样本和最相似的困难样本分开，去得到更均匀的表示。然而困难样本往往是与本样本相似程度较高的，很多困难负样本其实是潜在的正样本，过分强迫与困难样本分开会破坏学到的潜在语义结构，因此，温度系数不能过小 考虑两个极端情况，温度系数趋向于0时，对比损失退化为只关注最困难的负样本的损失函数；当温度系数趋向于无穷大时，对比损失对所有负样本都一视同仁，失去了困难样本关注的特性。 可以把不同的负样本想像成同极点电荷在不同距离处的受力情况，距离越近的点电荷受到的库伦斥力更大，而距离越远的点电荷受到的斥力越小。对比损失也是这样的。这种性质更有利于形成在超球面均匀分布的特征。

语言建模 (lena-voita.github.io)中有个小游戏可以看到随着温度的变化导致概率分布的变化

参考

CVPR2021自监督学习论文: 理解对比损失的性质以及温度系数的作用 - 知乎 (zhihu.com)