梯度下降法
梯度下降法
简介

批度梯度下降
其实就是一次将整个数据集进行梯度下降的迭代 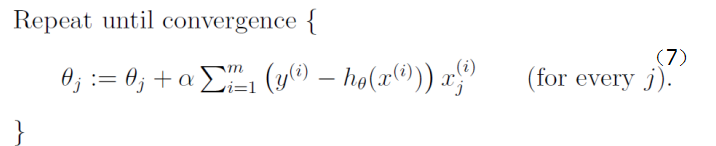 ## 随机梯度下降
就是对样本进行循环,每循环一个样本就更新一次参数,但是不容易收敛
## 随机梯度下降
就是对样本进行循环,每循环一个样本就更新一次参数,但是不容易收敛 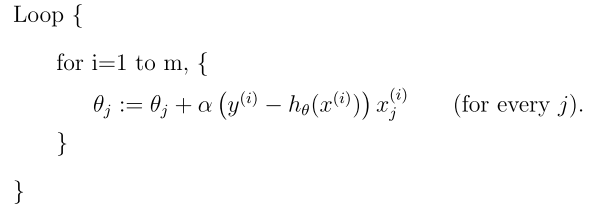
小批量梯度下降
大多数用于深度学习的梯度下降算法介于以上两者之间,使用一个以上而又不是全部的训练样本。传统上,这些会被称为小批量(mini-batch)或小批量随机(mini-batch stochastic)方法,现在通常将它们简单地成为随机(stochastic)方法。对于深度学习模型而言,人们所说的“随机梯度下降, SGD”,其实就是基于小批量(mini-batch)的随机梯度下降。
代码
以线性回归为例
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(42)
w = np.array([2, 1, 4, 5, 3])
d = len(w)
X = []
Y = []
for _ in range(1000000):
x = np.random.randn(d)
y = w.dot(x) + np.random.randn()
X.append(x)
Y.append(y)
X = np.array(X)
Y = np.array(Y)
def mse(y_true, y_test):
return ((y_true - y_test) ** 2) / len(y_true)
def gradient(y_true, y_test):
return 2 * (y_test - y_true) / len(y_true)
def batch_gradient_descent(w, alpha, x, y):
y_pred = x.dot(w)
error = mse(y, y_pred).mean()
grad = np.dot(x.T, gradient(y, y_pred))
w = w - alpha * grad
return w, error
def stochastic_gradient_descent(w, alpha, x, y, epoch):
alpha_update = alpha
for i in range(len(x)):
y_pred = x[i].dot(w)
grad = np.dot(x[i].T, (y_pred - y[i])) * 2 / len(x)
w = w- alpha_update * grad
alpha_update = alpha_update / (epoch+1)
error = mse(y, x.dot(w)).mean()
return w, error
X_test = []
Y_test = []
for _ in range(10000):
x = np.random.randn(d)
y = w.dot(x) + np.random.randn()
X_test.append(x)
Y_test.append(y)
X_test = np.array(X_test)
Y_test = np.array(Y_test)
def l2_mse(y_true, y_test, l, w):
return ((y_true - y_test) ** 2) / len(y_true) + l * np.sum(w ** 2)
def l2_gradient(y_true, y_test):
return 2 * (y_test - y_true) / len(y_true)
def batch_gradient_descent_with_l2(w, alpha, x, y, l):
y_pred = x.dot(w)
error = l2_mse(y, y_pred, l, w).mean()
grad = np.dot(x.T, l2_gradient(y, y_pred))
w = w - alpha * grad - alpha * l * w *2
return w, error
if __name__ == "__main__":
train_loss = []
test_loss = []
print("Batch Gradient Descent")
for epoch in range(1000):
w, error = batch_gradient_descent(w, 0.01, X, Y) # train
y_pred = X_test.dot(w)
error_test = mse(Y_test, y_pred).mean() # test
if epoch % 100 == 0:
print("Epoch: {}, TrainError: {}, TestError: {}".format(epoch, error, error_test))
train_loss.append(error)
test_loss.append(error_test)
plt.plot(train_loss, label="Train-No-L2")
plt.legend()
plt.xlabel("Epoch")
plt.ylabel("Loss")
plt.show()
plt.plot(test_loss, label="Test-No-L2")
plt.xlabel("Epoch")
plt.ylabel("Loss")
plt.legend()
plt.show()
plt.plot(train_loss, label="Train-No-L2")
plt.plot(test_loss, label="Test-No-L2")
plt.legend()
plt.show()
# ============================================
train_loss = []
test_loss = []
print("Batch Gradient Descent with L2")
l = 0.0001 # lambda
for epoch in range(1000):
w, error = batch_gradient_descent_with_l2(w, 0.01, X, Y, l) # train
y_pred = X_test.dot(w)
error_test = l2_mse(Y_test, y_pred, l, w).mean() # test
if epoch % 100 == 0:
print("Epoch: {}, TrainError: {}, TestError: {}".format(epoch, error, error_test))
train_loss.append(error)
test_loss.append(error_test)
plt.plot(train_loss, label="Train-L2")
plt.legend()
plt.xlabel("Epoch")
plt.ylabel("Loss")
plt.show()
plt.plot(test_loss, label="Test-L2")
plt.xlabel("Epoch")
plt.ylabel("Loss")
plt.legend()
plt.show()
plt.plot(train_loss, label="Train-L2")
plt.plot(test_loss, label="Test-L2")
plt.legend()
plt.show()