vllbc02显存占用计算
训练时
- 模型参数：我们模型的可学习权重。
- Optimizer states（优化器状态）：您需要跟踪的确切状态取决于您使用的优化器;例如，如果您使用的是 AdamW，则除了模型参数之外，您还需要跟踪第一和第二动量估计值。
- 模型激活值：这将根据您的网络架构和批处理大小而有所不同，但会显著影响内存使用。反向传播需要此信息，以便我们能够有效地计算梯度。
- 梯度：为模型的每个参数存储，与模型参数相同的内存占用。
- Input data：要传递给模型的 Importing 数据批次，内存占用取决于正在建模的数据的大小和类型。
图示：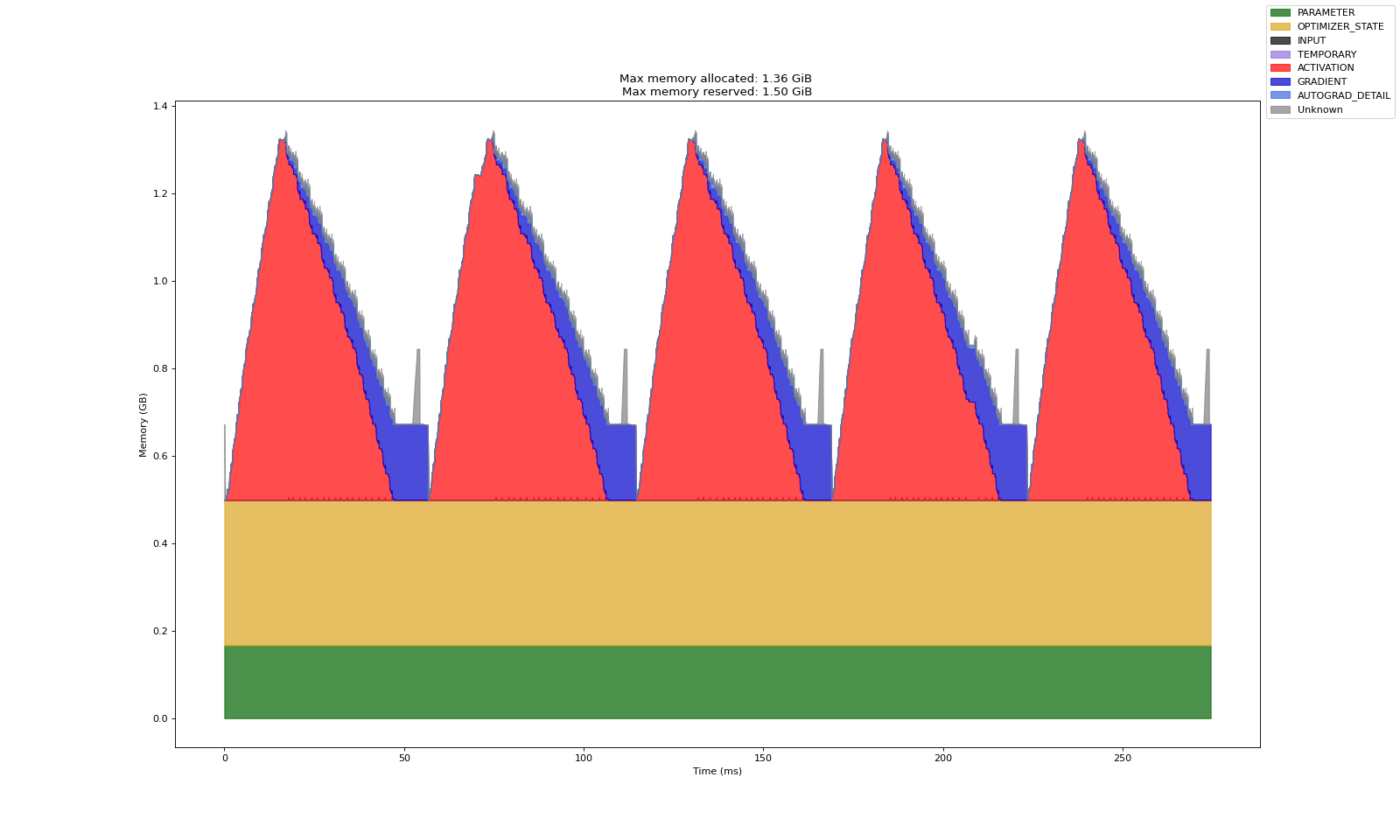 
具体数值： 对于一个 transformer
来说，参数量可以由以下公式给出（详见 transformer参数量分析）：
\[N=h*v+L*(12*h^2+13*h)+2*h\]
In that equation, \(h\) is the hidden dimension, \(v\) the vocabulary size, and \(L\) the number of layers in the model. Note that looking at the equation we can see that the term that will dominate with large hidden dimensions is the \(h^{2}\) term, since it’s the only one growing quadratically As we scale the parameters.
在全精度训练中（所有的存储单位都是 fp 32），优化器使用 adam 的情况下，模型部分我们需要存储：
\[\begin{aligned}&m_{params}=4*N\\&m_{grad}=4*N\\&m_{opt}=(4+4)*N\end{aligned}\]
而在使用混合精度的情况下，模型的参数和梯度使用 bf 16，为了稳定性，优化器还需要存储 fp 32 的模型参数，即：
\[\begin{aligned}&m_{params}=2*N\\&m_{grad}=2*N\\&m_{params\_fp32}=4*N\\&m_{opt} =(4+4)*N\end{aligned}\]
Some libraries store grads in FP32, which would require an additional mparams_fp32=4∗Nmparams_fp32=4∗N memory. This is done, for example, in Nanotron, because BF16 is lossy for smaller values and we always prioritize stability. See this DeepSpeed issue for more information.
也就是说有的库还实现了存储 fp 32 的梯度，考虑稳定性。
The FP32 copy of the parameters (mparams_fp32mparams_fp32) is sometimes called the “master weights” in the literature and codebases.
保存 fp 32 模型参数的原因是 bf 16 的精度不足以支持高效参数更新，fp 32 可以避免误差累计，保证优化器的数值稳定性和训练效果。具体分析如下（来自为什么LLM一般使用较大的权重衰减系数？）：
从浮点数的存储格式建立了「计算机浮点数的数值绝对值越大，则精度越低」的结论，对于深度学习训练过程（前向-反向-更新）来说： 如果使用低精度浮点数保存和更新模型参数时，如果模型参数绝对值比较大，而更新的步幅比较小，那么更新会由于舍入误差而失效，这就是为什么要维护一个 fp 32 的模型参数的原因。 并且从一个高精度的模型转化为低精度模型的时候，参数的绝对值越大，则丢失的精度越多。在模型更新了fp32的备份之后，还需要将fp32的权重转化为低精度的版本，参与后续的forward过程。由于浮点数的精度随着绝对值的增加而降低，因此参数的绝对值越大，在精度的转化中损失的精度也越多。此外，在前向和反向计算的过程中，激活值也会存在类似的精度损失问题。如果我们在训练过程中引入权重衰减，那么模型的权重的绝对值就可以得到一定的控制。除了提供一定的正则化效应之外，也能够降低由于模型的参数范数增长而导致的精度损失的风险。
混合精度训练示意图：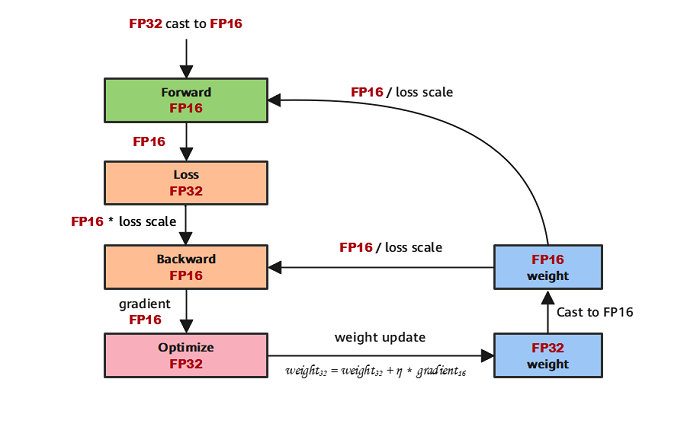 
1.
参数以FP32存储；这主要是因为，在基于梯度更新权重的时候，往往公式:权重
= 旧权重 + lr * 梯度，而在深度模型中，lr *
梯度这个值往往是非常小的，如果利用 fp16 来进行相加的话，
则很可能出现精度的问题，导致模型无法更新。因此参数以FP32的形式存储 2.
正向计算过程中，遇到FP16算子，需要把算子输入和参数从FP32
cast成FP16进行计算； 3. 将Loss层设置为FP32进行计算； 4.
反向计算过程中，首先乘以Loss Scale值，避免反向梯度过小而产生下溢； 5.
FP16参数参与梯度计算，其结果将被cast回FP32； 6. 除以Loss
scale值，还原被放大的梯度； 7.
判断梯度是否存在溢出，如果溢出则跳过更新，否则优化器以FP32对原始参数进行更新。
根据上述公式可以快速得到一些模型训练时占用显存：
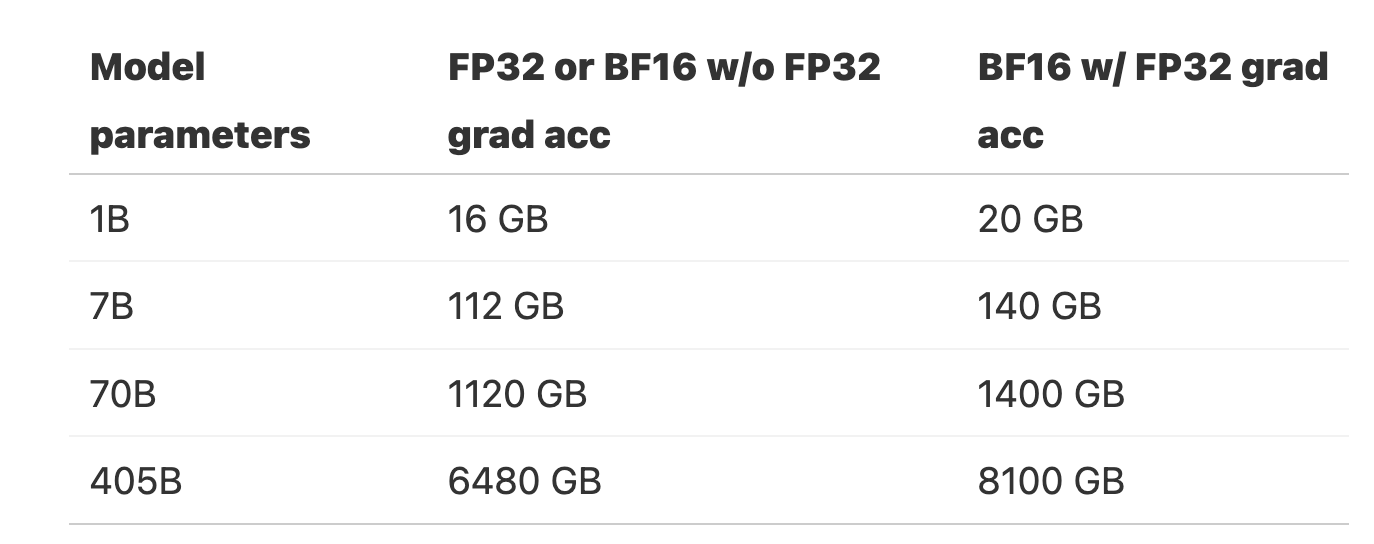
此外激活值也是显存的巨大杀手，随着句子长度的增加而增加，有以下的计算公式：
\[m_{act}=L\cdot seq\cdot bs\cdot h\cdot(34+\frac{5\cdot n_{heads}\cdot seq}h)\]
Here, \(L\) is the number of layers, seq the sequence length, \(bs\) the batch size in samples, \(h\) the hidden dimension of the model, and \(n_{heads}\) the number of heads.
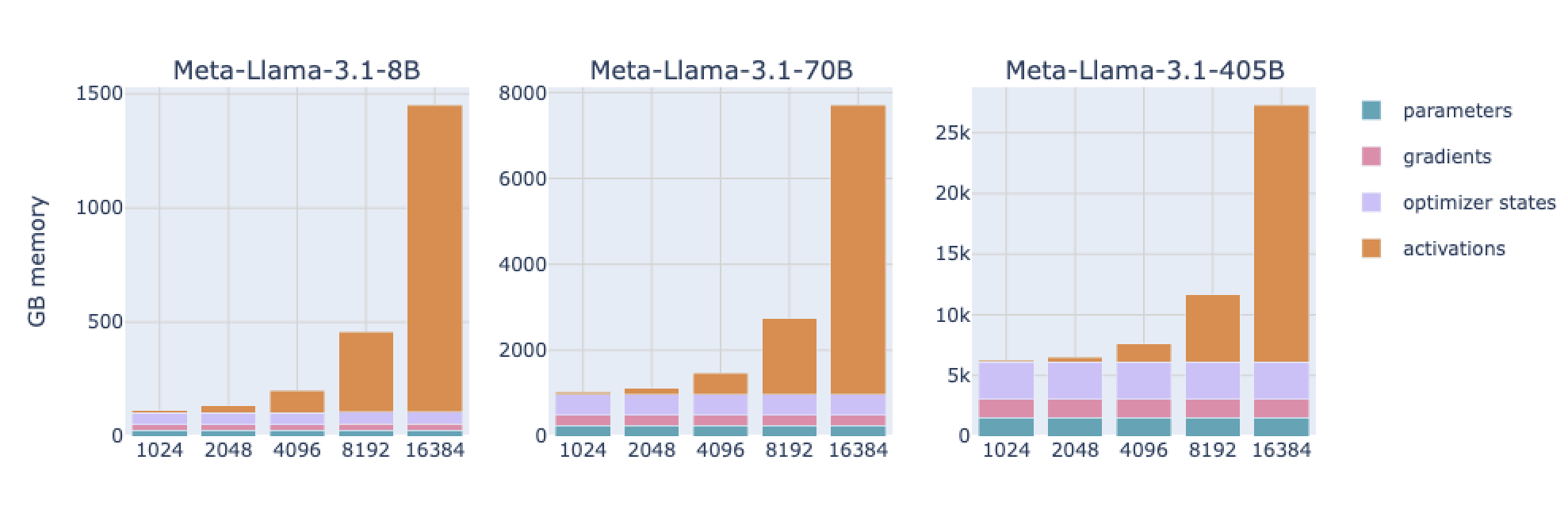
可见在长上下文的训练中，激活值才是显存最大的杀手。这就需要Activation checkpointing 来降低这部分的显存占用，详见 Activation checkpointing
推理时
一个经验法则是：推理时的峰值显存大致是模型参数显存的 1.5 - 2.5 倍（尤其在处理长序列或大批次时）。更精确的估计需要结合具体模型和输入
输入/输出的 Token 存储：需要显存存储输入的 Token 嵌入（embedding）和生成的输出 Token。
中间激活值（Intermediate Activations）：前向传播过程中每一层的输出（如 Attention 的 Key/Value 缓存、FFN 的中间结果等）。
Key-Value 缓存（KV Cache）：自回归生成时，为避免重复计算历史 Token 的 Key/Value，需缓存这些中间结果（显存占用与输入+输出长度成正比）
关于 kv cache 占用显存的计算，详见 KV cache ## 参考