主题模型

主题模型也可以看成一种词向量表达，主要有LSA、PLSA、LDA。按照这个顺序来逐渐发展的

词袋模型

将所有词语装进一个袋子里，不考虑其词法和语序的问题，即每个词语都是独立的

例子：

句子1：我 爱 北 京 天 安 门
转换为 [1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0]

句子2：我 喜 欢 上 海
转换为 [1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1]

from sklearn.feature_extraction.text import CountVectorizer
corpus = [
    'This is the first document.',
    'This document is the second document.',
    'And this is the third one.',
    'Is this the first document?',
]
vectorizer = CountVectorizer()
vectorizer.fit_transform(corpus).toarray()

结果：

[[0 1 1 1 0 0 1 0 1]
 [0 2 0 1 0 1 1 0 1]
 [1 0 0 1 1 0 1 1 1]
 [0 1 1 1 0 0 1 0 1]]

LSA

LSA就是潜在语义分析。特点是通过矩阵分解发现文本与单词之间基于主题（话题）的语义关系。 首先要清楚几个概念：

单词-文本矩阵

\[ X=\left[\begin{array}{cccc} x_{11} & x_{12} & \cdots & x_{1 n} \\\\ x_{21} & x_{22} & \cdots & x_{2 n} \\\\ \vdots & \vdots & & \vdots \\\\ x_{m 1} & x_{m 2} & \cdots & x_{m n} \end{array}\right] \]

这是一个 \(m \times n\) 矩阵, 元素 \(x_{i j}\) 表示单词 \(w_i\) 在文本 \(d_j\) 中出现的频数或权值。由于单 词的种类很多, 而每个文本中出现单词的种类通常较少, 所以单词-文本矩阵是一个稀 疏矩阵。 权值通常用单词频率-逆文本频率 (term frequency-inverse document frequency, TF-IDF）表示，其定义是

\[ \operatorname{TFIDF}_{i j}=\frac{\mathrm{tf}_{i j}}{\mathrm{tf}_{\bullet j}} \log \frac{\mathrm{df}}{\mathrm{df}_i}, \quad i=1,2, \cdots, m ; \quad j=1,2, \cdots, n \]

直观上讲，可以直接用每一列作为文本语义表达， 因此可以通过余弦相似度等计算文本之间的相似性，并且矩阵稀疏，计算量较少。但其并不关心文本中词语出现的顺序等信息，因此需要改进。 ### 单词-主题矩阵 假设所有文本共含有 \(k\) 个话题。假设每个话题由一个定义在单词集合 \(W\) 上的 \(m\) 维向量表示, 称为话题向量, 即

\[ t_l=\left[\begin{array}{c} t_{1 l} \\\\ t_{2 l} \\\\ \vdots \\\\ t_{m l} \end{array}\right], \quad l=1,2, \cdots, k \]

其中 \(t_{i l}\) 是单词 \(w_i\) 在话题 \(t_l\) 的权值, \(i=1,2, \cdots, m\), 权值越大, 该单词在该话题中 的重要度就越高。这 \(k\) 个话题向量 \(t_1, t_2, \cdots, t_k\) 张成一个话题向量空间 (topic vector 话题向量空间 \(T\) 也可以表示为一个矩阵, 称为单词-主题矩阵 (word-topic matrix）, 记作

\[ T=\left[\begin{array}{cccc} t_{11} & t_{12} & \cdots & t_{1 k} \\\\ t_{21} & t_{22} & \cdots & t_{2 k} \\\\ \vdots & \vdots & & \vdots \\\\ t_{m 1} & t_{m 2} & \cdots & t_{m k} \end{array}\right] \]

主题-文本矩阵

将单词-文本矩阵中的文本\(x_j\)投影到主题向量空间\(J\)中，得到在主题空间中的一个向量\(y_j\)。

\[ Y=\left[\begin{array}{cccc} y_{11} & y_{12} & \cdots & y_{1 n} \\\\ y_{21} & y_{22} & \cdots & y_{2 n} \\\\ \vdots & \vdots & & \vdots \\\\ y_{k 1} & y_{k 2} & \cdots & y_{k n} \end{array}\right] \]

从单词向量空间到主题向量空间的线性变换

单词-文本矩阵\(X\)可以近似表示为单词-主题矩阵\(T\)与主题-文本矩阵\(Y\)的乘积，这就是潜在语义分析：

\[ X\approx TY \]

潜在语义分析

给定单词-文本矩阵\(X\)，每一行代表一个单词，每一列代表一个文本。其中的元素代表单词在文本中的权重或者频数（词袋模型）。

截断奇异值分析

\[ X \approx U_k \Sigma_k V_k^{\mathrm{T}}=\left[\begin{array}{llll} u_1 & u_2 & \cdots & u_k \end{array}\right]\left[\begin{array}{cccc} \sigma_1 & 0 & 0 & 0 \\\\ 0 & \sigma_2 & 0 & 0 \\\\ 0 & 0 & \ddots & 0 \\\\ 0 & 0 & 0 & \sigma_k \end{array}\right]\left[\begin{array}{c} v_1^{\mathrm{T}} \\\\ v_2^{\mathrm{T}} \\\\ \vdots \\\\ v_k^{\mathrm{T}} \end{array}\right] \]

接下来考虑文本在主题空间中的表示。

\[ \begin{aligned} X &=\left[\begin{array}{llll} x_1 & x_2 & \cdots & x_n \end{array}\right] \approx U_k \Sigma_k V_k^{\mathrm{T}} \\\\ &=\left[\begin{array}{llll} u_1 & u_2 & \cdots & u_k \end{array}\right]\left[\begin{array}{cccc} \sigma_1 & & & \\\\ & \sigma_2 & 0 & \\\\ 0 & \ddots & \\\\ & & \sigma_k \end{array}\right]\left[\begin{array}{cccc} v_{11} & v_{21} & \cdots & v_{n 1} \\\\ v_{12} & v_{22} & \cdots & v_{n 2} \\\\ \vdots & \vdots & & \vdots \\\\ v_{1 k} & v_{2 k} & \cdots & v_{n k} \end{array}\right] \\\\ &=\left[\begin{array}{llll} u_1 & u_2 & \cdots & u_k \end{array}\right]\left[\begin{array}{cccc} \sigma_1 v_{11} & \sigma_1 v_{21} & \cdots & \sigma_1 v_{n 1} \\\\ \sigma_2 v_{12} & \sigma_2 v_{22} & \cdots & \sigma_2 v_{n 2} \\\\ \vdots & \vdots & & \vdots \\\\ \sigma_k v_{1 k} & \sigma_k v_{2 k} & \cdots & \sigma_k v_{n k} \end{array}\right] \end{aligned} \]

其中:

\[ u_l = \begin{bmatrix}u_{1l} \\\\u_{2l} \\\\ \vdots \\\\u_{ml} \end{bmatrix}, \quad l= 1, 2, \dots, k \]

代表单词对主题的权重。

由式知, 矩阵 \(X\) 的第 \(j\) 列向量 \(x_j\) 满足

\[ \begin{aligned} x_j & \approx U_k\left(\Sigma_k V_k^{\mathrm{T}}\right)\_j \\\\ &=\left[\begin{array}{llll} u_1 & u_2 & \cdots & u_k \end{array}\right]\left[\begin{array}{c} \sigma_1 v_{j 1} \\\\ \sigma_2 v_{j 2} \\\\ \vdots \\\\ \sigma_k v_{j k} \end{array}\right] \\\\ &=\sum_{l=1}^k \sigma_l v_{j l} u_l, \quad j=1,2, \cdots, n \end{aligned} \]

则\(\Sigma_kV_k^T\)每一个列向量是一个文本在主题向量空间中的表示。

PLSA

生成模型

假设有单词集合 \(W={w_1, w_2, \cdots, w_M}\), 其中 \(M\) 是单词个数; 文本 (指标) 集 合 \(D={d_1, d_2, \cdots, d_N}\), 其中 \(N\) 是文本个数; 话题集合 \(Z={z_1, z_2, \cdots, z_K}\), 其中 \(K\) 是预先设定的话题个数。随机变量 \(w\) 取值于单词集合; 随机变量 \(d\) 取值于文本集 合, 随机变量 \(z\) 取值于话题集合。概率分布 \(P(d)\) 、条件概率分布 \(P(z \mid d)\) 、条件概率分 布 \(P(w \mid z)\) 皆属于多项分布, 其中 \(P(d)\) 表示生成文本 \(d\) 的概率, \(P(z \mid d)\) 表示文本 \(d\) 生 成话题 \(z\) 的概率, \(P(w \mid z)\) 表示话题 \(z\) 生成单词 \(w\) 的概率。

每个文本 \(d\) 拥有自己的话题概率分布 \(P(z \mid d)\), 每个话题 \(z\) 拥有自己的单词概率分 布 \(P(w \mid z)\); 也就是说一个文本的内容由其相关话题决定, 一个话题的内容由其相关单词决定。

生成模型通过以下步骤生成文本-单词共现数据: (1) 依据概率分布 \(P(d)\), 从文本 (指标) 集合中随机选取一个文本 \(d\), 共生成 \(N\) 个文本; 针对每个文本, 执行以下操作; (2) 在文本 \(d\) 给定条件下, 依据条件概率分布 \(P(z \mid d)\), 从话题集合随机选取一个 话题 \(z\), 共生成 \(L\) 个话题, 这里 \(L\) 是文本长度; (3) 在话题 \(z\) 给定条件下, 依据条件概率分布 \(P(w \mid z)\), 从单词集合中随机选取一 个单词 \(w\) 。

生成模型中, 单词变量 \(w\) 与文本变量 \(d\) 是观测变量, 话题变量 \(z\) 是隐变量。也就 是说模型生成的是单词-话题-文本三元组 \((w, z, d)\) 的集合, 但观测到的是单词-文本二 元组 \((w, d)\) 的集合, 观测数据表示为单词-文本矩阵 \(T\) 的形式, 矩阵 \(T\) 的行表示单词, 列表示文本, 元素表示单词-文本对 \((w, d)\) 的出现次数。

从数据的生成过程可以推出, 文本-单词共现数据 \(T\) 的生成概率为所有单词-文本 对 \((w, d)\) 的生成概率的乘积,

\[ P(T)=\prod_{(w, d)} P(w, d)^{n(w, d)} \]

这里 \(n(w, d)\) 表示 \((w, d)\) 的出现次数, 单词-文本对出现的总次数是 \(N \times L\) 。每个单 词-文本对 \((w, d)\) 的生成概率由以下公式决定:

\[ \begin{aligned} P(w, d) &=P(d) P(w \mid d) \\\\ &=P(d) \sum_z P(w, z \mid d) \\\\ &=P(d) \sum_z P(z \mid d) P(w \mid z) \end{aligned} \]

即生成模型的定义。 生成模型假设在话题 \(z\) 给定条件下, 单词 \(w\) 与文本 \(d\) 条件独立, 即

\[ P(w, z \mid d)=P(z \mid d) P(w \mid z) \]

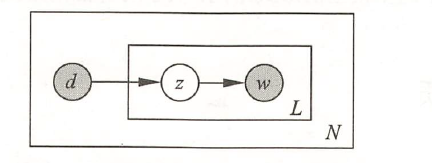
共现模型

\[ P(T)=\prod_{(w, d)} P(w, d)^{n(w, d)} \]

每个单词-文本对 \((w, d)\) 的概率由以下公式决定:

\[ P(w, d)=\sum_{z \in Z} P(z) P(w \mid z) P(d \mid z) \]

式 (18.5) 即共现模型的定义。容易验证, 生成模型 (18.2) 和共现模型 (18.5) 是等价的。 共现模型假设在话题 \(z\) 给定条件下, 单词 \(w\) 与文本 \(d\) 是条件独立的, 即

\[ P(w, d \mid z)=P(w \mid z) P(d \mid z) \]

直观解释：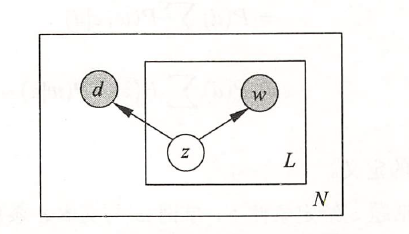

与潜在语义分析的关系

共现模型也可以表示为三个矩阵乘积的形式。这样, 概率潜在语义分析与 潜在语义分析的对应关系可以从中看得很清楚。下面是共现模型的矩阵乘积形式:

\[ \begin{aligned} X^{\prime} &=U^{\prime} \Sigma^{\prime} V^{\prime \mathrm{T}} \\\\ X^{\prime} &=[P(w, d)]\_{M \times N} \\\\ U^{\prime} &=[P(w \mid z)]\_{M \times K} \\\\ \Sigma^{\prime} &=[P(z)]\_{K \times K} \\\\ V^{\prime} &=[P(d \mid z)]\_{N \times K} \end{aligned} \]

概率潜在语义分析的算法

Plsa是含有隐变量的模型，其学习通常使用EM算法。 E步是计算Q函数，M步是极大化Q函数。

设单词集合为 \(W={w_1, w_2, \cdots, w_M}\), 文本集合为 \(D={d_1, d_2, \cdots, d_N}\), 话 题集合为 \(Z={z_1, z_2, \cdots, z_K}\) 。给定单词-文本共现数据 \(T={n\left(w_i, d_j\right)}, i=\) \(1,2, \cdots, M, j=1,2, \cdots, N\), 目标是估计概率潜在语义分析模型（生成模型）的 参数。如果使用极大似然估计, 对数似然函数是

\[ \begin{aligned} L &=\sum_{i=1}^M \sum_{j=1}^N n\left(w_i, d_j\right) \log P\left(w_i, d_j\right) \\\\ &=\sum_{i=1}^M \sum_{j=1}^N n\left(w_i, d_j\right) \log \left[\sum_{k=1}^K P\left(w_i \mid z_k\right) P\left(z_k \mid d_j\right)\right] \end{aligned} \]

但是模型含有隐变量, 对数似然函数的优化无法用解析方法求解, 这时使用 EM算法。 应用 EM算法的核心是定义 \(Q\) 函数。 \(\mathrm{E}\) 步：计算 \(Q\) 函数 \(Q\) 函数为完全数据的对数似然函数对不完全数据的条件分布的期望。针对概率潜 在语义分析的生成模型, \(Q\) 函数是

\[ Q=\sum_{k=1}^K{\sum_{j=1}^N n\left(d_j\right)\left[\log P\left(d_j\right)+\sum_{i=1}^M \frac{n\left(w_i, d_j\right)}{n\left(d_j\right)} \log P\left(w_i \mid z_k\right) P\left(z_k \mid d_j\right)\right]} P\left(z_k \mid w_i, d_j\right) \]

式中 \(n\left(d_j\right)=\sum_{i=1}^M n\left(w_i, d_j\right)\) 表示文本 \(d_j\) 中的单词个数, \(n\left(w_i, d_j\right)\) 表示单词 \(w_i\) 在文本 \(d_j\) 中出现的次数。条件概率分布 \(P\left(z_k \mid w_i, d_j\right)\) 代表不完全数据, 是已知变量。条件概 率分布 \(P\left(w_i \mid z_k\right)\) 和 \(P\left(z_k \mid d_j\right)\) 的乘积代表完全数据, 是末知变量。 由于可以从数据中直接统计得出 \(P\left(d_j\right)\) 的估计, 这里只考虑 \(P\left(w_i \mid z_k\right), P\left(z_k \mid d_j\right)\) 的估计, 可将 \(Q\) 函数简化为函数 \(Q^{\prime}\)

\[ Q^{\prime}=\sum_{i=1}^M \sum_{j=1}^N n\left(w_i, d_j\right) \sum_{k=1}^K P\left(z_k \mid w_i, d_j\right) \log \left[P\left(w_i \mid z_k\right) P\left(z_k \mid d_j\right)\right] \]

\(Q^{\prime}\) 函数中的 \(P\left(z_k \mid w_i, d_j\right)\) 可以根据贝叶斯公式计算

\[ P\left(z_k \mid w_i, d_j\right)=\frac{P\left(w_i \mid z_k\right) P\left(z_k \mid d_j\right)}{\sum_{k=1}^K P\left(w_i \mid z_k\right) P\left(z_k \mid d_j\right)} \]

其中 \(P\left(z_k \mid d_j\right)\) 和 \(P\left(w_i \mid z_k\right)\) 由上一步迭代得到。 \(\mathrm{M}\) 步: 极大化 \(Q\) 函数。 通过约束最优化求解 \(Q\) 函数的极大值, 这时 \(P\left(z_k \mid d_j\right)\) 和 \(P\left(w_i \mid z_k\right)\) 是变量。因为 变量 \(P\left(w_i \mid z_k\right), P\left(z_k \mid d_j\right)\) 形成概率分布, 满足约束条件

\[ \begin{aligned} &\sum_{i=1}^M P\left(w_i \mid z_k\right)=1, \quad k=1,2, \cdots, K \\\\ &\sum_{k=1}^K P\left(z_k \mid d_j\right)=1, \quad j=1,2, \cdots, N \end{aligned} \]

应用拉格朗日法, 引入拉格朗日乘子 \(\tau_k\) 和 \(\rho_j\), 定义拉格朗日函数 \(A\)

\[ \Lambda=Q^{\prime}+\sum_{k=1}^K \tau_k\left(1-\sum_{i=1}^M P\left(w_i \mid z_k\right)\right)+\sum_{j=1}^N \rho_j\left(1-\sum_{k=1}^K P\left(z_k \mid d_j\right)\right) \]

将拉格朗日函数 \(\Lambda\) 分别对 \(P\left(w_i \mid z_k\right)\) 和 \(P\left(z_k \mid d_j\right)\) 求偏导数, 并令其等于 0 , 得到下面 的方程组

\[ \begin{aligned} &\sum_{j=1}^N n\left(w_i, d_j\right) P\left(z_k \mid w_i, d_j\right)-\tau_k P\left(w_i \mid z_k\right)=0, \quad i=1,2, \cdots, M ; \quad k=1,2, \cdots, K \\\\ &\sum_{i=1}^M n\left(w_i, d_j\right) P\left(z_k \mid w_i, d_j\right)-\rho_j P\left(z_k \mid d_j\right)=0, \quad j=1,2, \cdots, N ; \quad k=1,2, \cdots, K \end{aligned} \]

解方程组得到 \(M\) 步的参数估计公式:

\[ P\left(w_i \mid z_k\right)=\frac{\sum_{j=1}^N n\left(w_i, d_j\right) P\left(z_k \mid w_i, d_j\right)}{\sum_{m=1}^M \sum_{j=1}^N n\left(w_m, d_j\right) P\left(z_k \mid w_m, d_j\right)} \]

\[ P(z_k\mid d_j) = \frac{\sum_{i=1}^Mn(w_i, d_j)P(z_k\mid w_i,d_j)}{n(d_j)} \]

总结算法

输入: 设单词集合为 \(W={w_1, w_2, \cdots, w_M}\), 文本集合为 \(D={d_1, d_2, \cdots, d_N}\), 话题集合为 \(Z={z_1, z_2, \cdots, z_K}\), 共现数据 \({n\left(w_i, d_j\right)}, i=1,2, \cdots, M, j=1\), \(2, \cdots, N\); 输出: \(P\left(w_i \mid z_k\right)\) 和 \(P\left(z_k \mid d_j\right)\) 。 (1) 设置参数 \(P\left(w_i \mid z_k\right)\) 和 \(P\left(z_k \mid d_j\right)\) 的初始值。 (2) 迭代执行以下 \(\mathrm{E}\) 步, \(\mathrm{M}\) 步, 直到收敛为止。 \(\mathrm{E}\) 步:

\[ P\left(z_k \mid w_i, d_j\right)=\frac{P\left(w_i \mid z_k\right) P\left(z_k \mid d_j\right)}{\sum_{k=1}^K P\left(w_i \mid z_k\right) P\left(z_k \mid d_j\right)} \]

M 步:

\[ \begin{aligned} P\left(w_i \mid z_k\right) &=\frac{\sum_{j=1}^N n\left(w_i, d_j\right) P\left(z_k \mid w_i, d_j\right)}{\sum_{m=1}^M \sum_{j=1}^N n\left(w_m, d_j\right) P\left(z_k \mid w_m, d_j\right)} \\\\ P\left(z_k \mid d_j\right) &=\frac{\sum_{i=1}^M n\left(w_i, d_j\right) P\left(z_k \mid w_i, d_j\right)}{n\left(d_j\right)} \end{aligned} \]

用法

与LSA类似，可以把文档对各个主题的概率看作是文档的表示，最后用到的就是\(P(z_k\mid d_j)\)。

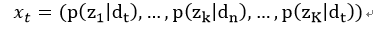k就是我们自己设定的主题数，一般来说K远远小于文档个数和词汇表大小，这样也达到了降维的目的。

优点与不足

优点

pLSA是在一套比较完整的思想的基础上提出来的，模型中各项参数有明确的物理含义，可解释性比较强。相比LSA，pLSA对人类生成文本机制的刻画更加细致、更加符合我们的常识，比如，pLSA基于条件概率，引入了一个“隐含变量”（相对于可以看到的文档和词语，是不可观测变的），即主题，来描述文本生成的过程。 #### 不足 pLSA的理论与我们的实践不是那么的统一: (1) 我们说话的时候，根本不会考虑” 我说这段话的概率大小”，即 \(p\left(d_t\right)\) (2) pLSA认为，我们说话时面向的主题分布，取决于 “文档” （实际上是文档ID)。这个假设显然是不合理的，小说家不会因为自己写到第666回而调整 主题。 (3) 类似 (2)，随着上下文的变化，我们围绕一个主题说话的内容和方式也 会发生改变。在主题模型中，这种改变的体现，就是一个主题下的词语概率分 布会发生改变。而pLSA忽略了这样的事实。

从计算复杂度的角度看pLSA有两个比较大的缺陷: (1) pLSA中，对文档 出现的概率估计，来自对训练语料的学习。而对于一个 末知文档，我们是无法估计它出现的概率的一一因此pLSA无法对训练语料之 外的文档进行处理。pLSA的这个特点决定了，在在线(online) 场景中(数据是 持续增加的)，那么文档处理系统就需要定时使用pLSA对整个语料库进行计 算。因此，pLSA比较适合允许一定时滞的离线计算。 (2) pLSA认为一个文档对各个主题的隶属度是一定的——而一个主题对各个词语的隶属度也是一定的，因此pLSA在生成一个文档的各个词语时、使用了相同的词语概率分布。这样，pLSA需要为每一个文档记录一个专门的随着语料数据集规模的增加，pLSA的参数规模也会增加，导致模型训练越来越困难。

LDA

LDA模型是文本集合的生成概率模型。

LDA 的文本集合的生成过程如下: 首先随机生成一个文本的话题分布, 之后在该 文本的每个位置, 依据该文本的话题分布随机生成一个话题, 然后在该位置依据该话 题的单词分布随机生成一个单词, 直至文本的最后一个位置, 生成整个文本。重复以 上过程生成所有文本。

LDA 模型是含有隐变量的概率图模型。模型中, 每个话题的单词分布, 每个文 本的话题分布, 文本的每个位置的话题是隐变量; 文本的每个位置的单词是观测变 量。LDA 模型的学习与推理无法直接求解, 通常使用吉布斯抽样 (Gibbs sampling) 和 变分 EM算法 (variational EM algorithm), 前者是蒙特卡罗法, 而后者是近似算法。

多项分布

(多项分布) 若多元离散随机变量 \(X=\left(X_1, X_2, \cdots, X_k\right)\) 的概率质 量函数为

\[ \begin{aligned} P\left(X_1=n_1, X_2=n_2, \cdots, X_k=n_k\right) &=\frac{n !}{n_{1} ! n_{2} ! \cdots n_{k} !} p_1^{n_1} p_2^{n_2} \cdots p_k^{n_k} \\\\ &=\frac{n !}{\prod_{i=1}^k n_{i} !} \prod_{i=1}^k p_i^{n_i} \end{aligned} \]

其中 \(p=\left(p_1, p_2, \cdots, p_k\right), p_i \geqslant 0, i=1,2, \cdots, k, \sum_{i=1}^k p_i=1, \sum_{i=1}^k n_i=n\), 则称随机变 量 \(X\) 服从参数为 \((n, p)\) 的多项分布, 记作 \(X \sim \operatorname{Mult}(n, p)\) 。

当试验的次数 \(n\) 为 1 时, 多项分布变成类别分布 (categorical distribution)。类 别分布表示试验可能出现的 \(k\) 种结果的概率。显然多项分布包含类别分布。

狄利克雷分布

狄利克雷分布 (Dirichlet distribution) 是一种多元连续随机变量的概率分布, 是 贝塔分布 (beta distribution) 的扩展。在贝叶斯学习中, 狄利克雷分布常作为多项分 布的先验分布使用。 (狄利克雷分布) 若多元连续随机变量 \(\theta=\left(\theta_1, \theta_2, \cdots, \theta_k\right)\) 的概率密 度函数为

\[ p(\theta \mid \alpha)=\frac{\Gamma\left(\sum_{i=1}^k \alpha_i\right)}{\prod_{i=1}^k \Gamma\left(\alpha_i\right)} \prod_{i=1}^k \theta_i^{\alpha_i-1} \]

其中 \(\sum_{i=1}^k \theta_i=1, \theta_i \geqslant 0, \alpha=\left(\alpha_1, \alpha_2, \cdots, \alpha_k\right), \alpha_i>0, i=1,2, \cdots, k\), 则称随机变量 \(\theta\) 服从参数为 \(\alpha\) 的狄利克雷分布, 记作 \(\theta \sim \operatorname{Dir}(\alpha)\) 。 式中 \(\Gamma(s)\) 是伽马函数, 定义为

\[ \Gamma(s)=\int_0^{\infty} x^{s-1} \mathrm{e}^{-x} \mathrm{~d} x, \quad s>0 \]

具有性质：

\[ \Gamma(s+1) = s\Gamma(s) \]

当s为自然数时，有：

\[ \Gamma(s+1) = s! \]

令

\[ \mathrm{B}(\alpha)=\frac{\prod_{i=1}^k \Gamma\left(\alpha_i\right)}{\Gamma\left(\sum_{i=1}^k \alpha_i\right)} \]

则狄利克雷分布的密度函数可以写成

\[ p(\theta \mid \alpha)=\frac{1}{\mathrm{~B}(\alpha)} \prod_{i=1}^k \theta_i^{\alpha_i-1} \]

\(\mathrm{B}(\alpha)\) 是规范化因子, 称为多元贝塔函数 (或扩展的贝塔函数)。由密度函数的性质

\[ \int \frac{\Gamma\left(\sum_{i=1}^k \alpha_i\right)}{\prod_{i=1}^k \Gamma\left(\alpha_i\right)} \prod_{i=1}^{\alpha_i-1} \mathrm{~d} \theta=\frac{\Gamma\left(\sum_{i=1}^k \alpha_i\right)}{\prod_{i=1}^k \Gamma\left(\alpha_i\right)} \int \prod_{i=1}^k \theta_i^{\alpha_i-1} \mathrm{~d} \theta=1 \]

得

\[ \mathrm{B}(\alpha)=\int \prod_{i=1}^k \theta_i^{\alpha_i-1} \mathrm{~d} \theta \]

二项分布与贝塔分布

二项分布是多项分布的特殊情况, 贝塔分布是狄利克雷分布的特殊情况。 二项分布是指如下概率分布。 \(X\) 为离散随机变量, 取值为 \(m\), 其概率质量函数为

\[ P(X=m)=\left(\begin{array}{c} n \\\\ m \end{array}\right) p^m(1-p)^{n-m}, \quad m=0,1,2, \cdots, n \]

其中 \(n\) 和 \(p(0 \leqslant p \leqslant 1)\) 是参数。

贝塔分布是指如下概率分布, \(X\) 为连续随机变量, 取值范围为 \([0,1]\), 其概率密度 函数为

\[ p(x)= \begin{cases}\frac{1}{\mathrm{~B}(s, t)} x^{s-1}(1-x)^{t-1}, & 0 \leqslant x \leqslant 1 \\\\ 0, & \text { 其他 }\end{cases} \]

其中 \(s>0\) 和 \(t>0\) 是参数, \(\mathrm{B}(s, t)=\frac{\Gamma(s) \Gamma(t)}{\Gamma(s+t)}\) 是贝塔函数, 定义为

\[ \mathrm{B}(s, t)=\int_0^1 x^{s-1}(1-x)^{t-1} \mathrm{~d} x = \frac{\Gamma(s)\Gamma(t)}{\Gamma(s+t)} \]

当 \(s, t\) 是自然数时(\(\Gamma(s+1) = s!\)),

\[ \mathrm{B}(s, t)=\frac{(s-1) !(t-1) !}{(s+t-1) !} \]

当 \(n\) 为 1 时, 二项分布变成伯努利分布（Bernoulli distribution）或 0-1 分布。 伯努利分布表示试验可能出现的 2 种结果的概率。显然二项分布包含伯努利分布。给出几种概率分布的关系。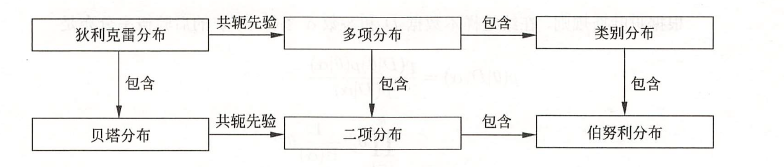

基本想法

在LDA主题模型下，一篇文章由词语的序列组成。首先以一定概率选择一个主题，其次以一定概率在这个主题中选择一个词。如果一篇文章由1000个词组成，那么就把上述方式重复1000遍，就能组成这篇文章。那么值得注意的是，以一定概率选择一个主题是服从多项式分布的，而多项式分布的参数是服从Dirichlet分布的。以一定概率在特定主题中选择一个词也是服从多项式分布的，多项式分布的参数是服从Dirichlet分布的。为什么呢？因为Dirichlet分布是多项式分布的共轭分布，也就是说由贝叶斯估计得到的后验分布仍然是Dirichlet分布。

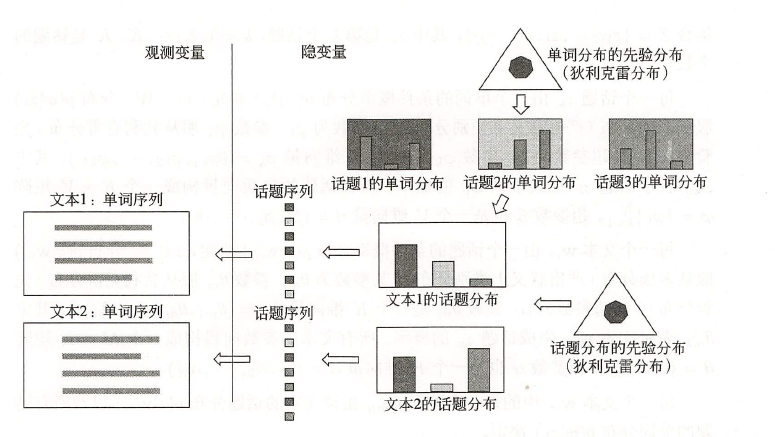
LDA与PLSA的关系

二者都是概率模型，都是利用概率生成模型对文本集合进行主题分析的无监督学习方法。

PLSA是用了频率派的方法，利用极大似然进行学习，而LDA使用了贝叶斯派的方法，进行贝叶斯推断。

二者都假设存在两个分布：话题是单词的多项分布，文本是话题的多项分布，不同的在于LDA认为多项分布的参数也服从一个分布，而不是固定不变的，使用狄利克雷分布作为多项分布的先验分布，也就是多项分布的参数服从狄利克雷分布。

引入先验概率的作用可以防止过拟合。为啥选择狄利克雷分布呢？因为它是多项分布的共轭先验分布，先验分布与后验分布形式相同，便于由先验分布得到后验分布。

LDA是在Plsa的基础上，为单词分布和主题分布增加了两个狄利克雷先验。

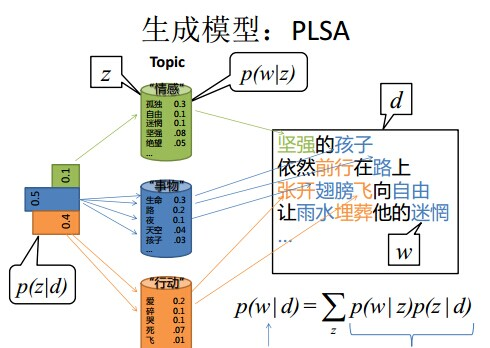
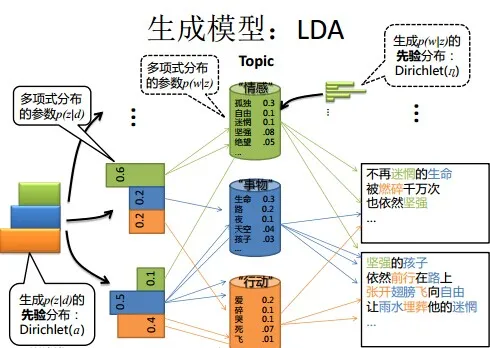
模型定义

模型要素

潜在狄利克雷分配 (LDA) 使用三个集合: 一是单词集合 \(W={w_1, \cdots, w_v, \cdots}\), , 其中 \(w_v\) 是第 \(v\) 个单词, \(v=1,2, \cdots, V, V\) 是单词的个数。二是文本集合 \(D={\mathbf{w}_1, \cdots, \mathbf{w}_m, \cdots, \mathbf{w}_M}\), 其中 \(\mathbf{w}_m\) 是第 \(m\) 个文本, \(m=1,2, \cdots, M, M\) 是文本 的个数。文本 \(\mathbf{w}_m\) 是一个单词序列 \(\mathbf{w}_m=\left(w_{m 1}, \cdots, w_{m n}, \cdots, w_{m N_m}\right)\), 其中 \(w_{m n}\) 是 文本 \(\mathbf{w}_m\) 的第 \(n\) 个单词, \(n=1,2, \cdots, N_m, N_m\) 是文本 \(\mathbf{w}_m\) 中单词的个数。三是主题集合集合 \(Z={z_1, \cdots, z_k, \cdots, z_K}\), 其中 \(z_k\) 是第 \(k\) 个话题, \(k=1,2, \cdots, K, K\) 是话题的个数。

• 每一个话题 \(z_k\) 由一个单词的条件概率分布 \(p\left(w \mid z_k\right)\) 决定, \(w \in W\) 。分布 \(p\left(w \mid z_k\right)\) 服从多项分布 (严格意义上类别分布), 其参数为 \(\varphi_k\) 。参数 \(\varphi_k\) 服从狄利克雷分布 (先验分布), 其超参数为 \(\beta\) 。参数 \(\varphi_k\) 是一个 \(V\) 维向量 \(\varphi_k=\left(\varphi_{k 1}, \varphi_{k 2}, \cdots, \varphi_{k V}\right)\), 其中 \(\varphi_{k v}\) 表示话题 \(z_k\) 生成单词 \(w_v\) 的概率。所有话题的参数向量构成一个 \(K \times V\) 矩阵 \(\varphi=\{\varphi_k\}_{k=1}^K\) 。超参数 \(\beta\) 也是一个 \(V\) 维向量 \(\beta=\left(\beta_1, \beta_2, \cdots, \beta_V\right)\_{\text {。 }}\)(对于话题\(z_k\)其生成单词\(w_v\)先验服从狄利克雷分布，因此是一个V维向量)
• 每一个文本 \(\mathbf{w}_m\) 由一个话题的条件概率分布 \(p\left(z \mid \mathbf{w}_m\right)\) 决定, \(z \in Z_{\text {。 }}\) 分布 \(p\left(z \mid \mathbf{w}_m\right)\) 服从多项分布 (严格意义上类别分布), 其参数为 \(\theta_m\) 。参数 \(\theta_m\) 服从狄利克雷分布 (先验分布), 其超参数为 \(\alpha\) , 参数 \(\theta_m\) 是一个 \(K\) 维向量 \(\theta_m=\left(\theta_{m 1}, \theta_{m 2}, \cdots, \theta_{m K}\right)\), 其中 \(\theta_{m k}\) 表示文本 \(\mathrm{w}_m\) 生成话题 \(z_k\) 的概率。所有文本的参数向量构成一个 \(M \times K\) 矩阵 \(\theta=\{\theta_m\}_{m=1}^M\) 。超参数 \(\alpha\) 也是一个 \(K\) 维向量 \(\alpha=\left(\alpha_1, \alpha_2, \cdots, \alpha_K\right)\) 。
• 每一个文本 \(\mathbf{w}_m\) 中的每一个单词 \(w_{m n}\) 由该文本的话题分布 \(p\left(z \mid \mathbf{w}_m\right)\) 以及所有话 题的单词分布 \(p\left(w \mid z_k\right)\) 决定。

生成过程

LDA 文本集合的生成过程如下: 给定单词集合 \(W\), 文本集合 \(D\), 话题集合 \(Z\), 狄利克雷分布的超参数 \(\alpha\) 和 \(\beta\) 。

1.生成单词分布 随机生成 \(K\) 个话题的单词分布。具体过程如下, 按照狄利克雷分布 \(\operatorname{Dir}(\beta)\) 随机 生成一个参数向量 \(\varphi_k, \varphi_k \sim \operatorname{Dir}(\beta)\), 作为话题 \(z_k\) 的单词分布 \(p\left(w \mid z_k\right), w \in W, k=\) \(1,2, \cdots, K\) 。

2.生成主题分布 随机生成 \(M\) 个文本的主题分布。具体过程如下: 按照狄利克雷分布 \(\operatorname{Dir}(\alpha)\) 随 机生成一个参数向量 \(\theta_m, \theta_m \sim \operatorname{Dir}(\alpha)\), 作为文本 \(\mathbf{w}_m\) 的主题分布 \(p\left(z \mid \mathbf{w}_m\right), m=\) \(1,2, \cdots, M_{}\) 。

3.生成文本的单词序列 随机生成 \(M\) 个文本的 \(N_m\) 个单词。文本 \(\mathbf{w}_m(m=1,2, \cdots, M)\) 的单词 \(w_{m n}(n=\) \(\left.1,2, \cdots, N_m\right)\) 的生成过程如下:

3.1 首先按照多项分布 \(\operatorname{Mult}\left(\theta_m\right)\) 随机生成一个话题 \(z_{m n}, z_{m n} \sim \operatorname{Mult}\left(\theta_m\right)\) 3.2 然后按照多项分布 \(\operatorname{Mult}\left(\varphi_{z_{m n}}\right)\) 随机生成一个单词 \(w_{m n}, w_{m n} \sim \operatorname{Mult}\left(\varphi_{z_{m n}}\right)\_{\text {。 }}\) 文本 \(\mathbf{w}_m\) 本身是单词序列 \(\mathbf{w}_m=\left(w_{m 1}, w_{m 2}, \cdots, w_{m N_m}\right)\), 对应着隐式的话题序列 \(\mathbf{z}_m=\left(z_{m 1}, z_{m 2}, \cdots, z_{m N_m}\right) 。\)

引用一下LDA数学八卦的图：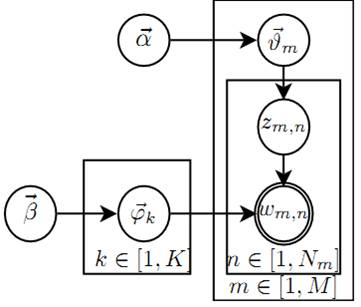

• \(\vec{\alpha} \rightarrow \vec{\theta}_m \rightarrow z_{m, n}\), 这个过程表示在生成第 \(m\) 篇文档的时候，先从第一个坛子中抽了一个doc-topic 骰子 \(\vec{\theta}_m\),然后投这个骰子生成了文档\(m\)中第 \(n\) 个词的topic编号 \(z_{m, n}\) ；
• \(\vec{\beta} \rightarrow \vec{\varphi}_k \rightarrow w_{m, n} \mid k=z_{m, n}\), 这个过程表示用如下动作生成语料中第 \(m\) 篇文档的第 \(n\) 个词: 在上帝手头的 \(K\) 个topic-word 骰子 \(\vec{\varphi}_k\) 中，挑选编号为 \(k=z_{m, n}\) 的那个骰子进行投掷，然后生成 word \(w_{m, n}\) ;

理解 LDA最重要的就是理解这两个物理过程。LDA 模型在基于 \(K\) 个 topic 生成语料中的 \(M\) 篇文档的过程中， 由于是 bag-of-words 模型，有一些物理过程是相互独立可交换的。由此，LDA生成模型中， \(M\) 篇文档会对应 于 \(M\) 个独立的 Dirichlet-Multinomial 共轭结构；K个 个 topic 会对应于 \(K\) 个独立的 Dirichlet-Multinomial 共轭结 构。所以理解 LDA 所需要的所有数学就是理解 Dirichlet-Multiomail 共轭，其它都就是理解物理过程。

总结

1. 对于话题 \(z_k(k=1,2, \cdots, K)\) : 生成多项分布参数 \(\varphi_k \sim \operatorname{Dir}(\beta)\), 作为话题的单词分布 \(p\left(w \mid z_k\right)\);
2. 对于文本 \(\mathbf{w}_m(m=1,2, \cdots, M)\); 生成多项分布参数 \(\theta_m \sim \operatorname{Dir}(\alpha)\), 作为文本的话题分布 \(p\left(z \mid \mathbf{w}_m\right)\);
3. 对于文本 \(\mathbf{w}_m\) 的单词 \(w_{m n}\left(m=1,2, \cdots, M, n=1,2, \cdots, N_m\right)\) :
   1. 采样生成话题 \(z_{m n} \sim \operatorname{Mult}\left(\theta_m\right)\), 作为单词对应的话题;
   2. 采样生成单词 \(w_{m n} \sim \operatorname{Mult}\left(\varphi_{z_{m n}}\right)\) 。

LDA 的文本生成过程中, 假定话题个数 \(K\) 给定, 实际通常通过实验选定。狄利 克雷分布的超参数 \(\alpha\) 和 \(\beta\) 通常也是事先给定的。在没有其他先验知识的情况下, 可以 假设向量 \(\alpha\) 和 \(\beta\) 的所有分量均为 1 , 这时的文本的话题分布 \(\theta_m\) 是对称的, 话题的单 词分布 \(\varphi_k\) 也是对称的。

（帮助理解：主题数为3，假设\(\theta_m\) = {0.4, 0.5, 0.1}，则说明主题\(z_2\)出现在文档m当中的概率为0.5，这就是多项分布的参数，再根据多项分布进行采样得到主题。）

概率计算

LDA 模型整体是由观测变量和隐变量组成的联合概率分布, 可以表为

\[ p(\mathbf{w}, \mathbf{z}, \theta, \varphi \mid \alpha, \beta)=\prod_{k=1}^K p\left(\varphi_k \mid \beta\right) \prod_{m=1}^M p\left(\theta_m \mid \alpha\right) \prod_{n=1}^{N_m} p\left(z_{m n} \mid \theta_m\right) p\left(w_{m n} \mid z_{m n}, \varphi\right) \]

(其中M为文本数，\(N_m\)为文档m的长度，K为主题数) 其中观测变量 \(\mathrm{w}\) 表示所有文本中的单词序列, 隐变量 \(\mathrm{z}\) 表示所有文本中的话题序列, 隐变量 \(\theta\) 表示所有文本的话题分布的参数, 隐变量 \(\varphi\) 表示所有话题的单词分布的参 数, \(\alpha\) 和 \(\beta\) 是超参数。

• \(p\left(\varphi_k \mid \beta\right)\) 表示超参数 \(\beta\) 给定条件下第 \(k\) 个话题的单词分布的参数 \(\varphi_k\) 的生成概率;
• \(p\left(\theta_m \mid \alpha\right)\) 表示超参数 \(\alpha\) 给定条件下第 \(m\) 个文本的话题分布的 参数 \(\theta_m\) 的生成概率;
• \(p\left(z_{m n} \mid \theta_m\right)\) 表示第 \(m\) 个文本的话题分布 \(\theta_m\) 给定条件下文本的 第 \(n\) 个位置的话题 \(z_{m n}\) 的生成概率;
• \(p\left(w_{m n} \mid z_{m n}, \varphi\right)\) 表示在第 \(m\) 个文本的第 \(n\) 个位 置的话题 \(z_{m n}\) 及所有话题的单词分布的参数 \(\varphi\) 给定条件下第 \(m\) 个文本的第 \(n\) 个位 置的单词 \(w_{m n}\) 的生成概率。

第 \(m\) 个文本的联合概率分布可以表为

\[ p\left(\mathbf{w}_m, \mathbf{z}_m, \theta_m, \varphi \mid \alpha, \beta\right)=\prod_{k=1}^K p\left(\varphi_k \mid \beta\right) p\left(\theta_m \mid \alpha\right) \prod_{n=1}^{N_m} p\left(z_{m n} \mid \theta_m\right) p\left(w_{m n} \mid z_{m n}, \varphi\right) \]

其中 \(\mathbf{w}_m\) 表示该文本中的单词序列, \(\mathbf{z}_m\) 表示该文本的话题序列, \(\theta_m\) 表示该文本的话 题分布参数。 LDA 模型的联合分布含有隐变量, 对隐变量进行积分得到边缘分布。 参数 \(\theta_m\) 和 \(\varphi\) 给定条件下第 \(m\) 个文本的生成概率是

\[ p\left(\mathbf{w}_m \mid \theta_m, \varphi\right)=\prod_{n=1}^{N_m}\left[\sum_{k=1}^K p\left(z_{m n}=k \mid \theta_m\right) p\left(w_{m n} \mid \varphi_k\right)\right] \]

超参数 \(\alpha\) 和 \(\beta\) 给定条件下第 \(m\) 个文本的生成概率是

\[ p\left(\mathbf{w}_m \mid \alpha, \beta\right)=\prod_{k=1}^K \int p\left(\varphi_k \mid \beta\right)\left[\int p\left(\theta_m \mid \alpha\right) \prod_{n=1}^{N_m}\left[\sum_{l=1}^K p\left(z_{m n}=l \mid \theta_m\right) p\left(w_{m n} \mid \varphi_l\right)\right] \mathrm{d} \theta_m\right] \mathrm{d} \varphi_k \]

超参数 \(\alpha\) 和 \(\beta\) 给定条件下所有文本的生成概率是

\[ p(\mathbf{w} \mid \alpha, \beta)=\prod_{k=1}^K \int p\left(\varphi_k \mid \beta\right)\left[\prod_{m=1}^M \int p\left(\theta_m \mid \alpha\right) \prod_{n=1}^{N_m}\left[\sum_{l=1}^K p\left(z_{m n}=l \mid \theta_m\right) p\left(w_{m n} \mid \varphi_l\right)\right] \mathrm{d} \theta_m\right] \mathrm{d} \varphi_k \]

吉布斯抽样

基本思想

有三个主要目标： - 话题序列的集合\(z=(z_1, z_2, \cdots, z_M)\)的后验概率分布，其中\(z_m\)是第m个文本的主题序列，\(z_m=(z_{m1}, \cdots, z_{mN_{m}})\); - 参数\(\theta=(\theta_1, \cdots, \theta_{M})\)，其中\(\theta_m\)是第m个文本的主题分布的参数； - 参数\(\varphi=(\varphi_1, \cdots, \varphi_K)\)，其中\(\varphi_k\)是第k个主题的单词分布的参数。

对\(p(\mathbf{w}, \mathbf{z}, \theta, \varphi \mid \alpha, \beta)\)进行估计

吉布斯抽样, 这是一种常用的马尔可夫链蒙特卡罗法。为了估计 多元随机变量 \(x\) 的联合分布 \(p(x)\), 吉布斯抽样法选择 \(x\) 的一个分量, 固定其他分量, 按照其条件概率分布进行随机抽样, 依次循环对每一个分量执行这个操作, 得到联合 分布 \(p(x)\) 的一个随机样本, 重复这个过程, 在燃烧期之后, 得到联合概率分布 \(p(x)\) 的 样本集合。

LDA 模型的学习通常采用收缩的吉布斯抽样 (collapsed Gibbs sampling) , 基本想法是, 通过对隐变量 \(\theta\) 和 \(\varphi\) 积分, 得到边缘概率分布 \(p(\mathbf{w}, \mathbf{z} \mid \alpha, \beta)\) (也是联合分 布), 其中变量 \(\mathbf{w}\) 是可观测的, 变量 \(\mathbf{z}\) 是不可观测的; 对后验概率分布 \(p(\mathbf{z} \mid \mathbf{w}, \alpha, \beta)\) 进 行吉布斯抽样, 得到分布 \(p(\mathbf{z} \mid \mathbf{w}, \alpha, \beta)\) 的样本集合; 再利用这个样本集合对参数 \(\theta\) 和 \(\varphi\) 进行估计, 最终得到 LDA 模型 \(p(\mathbf{w}, \mathbf{z}, \theta, \varphi \mid \alpha, \beta)\) 的所有参数估计。 #### 算法流程

输入: 文本的单词序列 \(\mathbf{w}=\{\mathbf{w}_1, \cdots, \mathbf{w}_m, \cdots, \mathbf{w}_M\}, \mathbf{w}_m=\left(w_{m 1}, \cdots, w_{m n}, \cdots\right.\), \(\left.w_{m_{N_m}}\right)\);

输出: 文本的话题序列 \(\mathrm{z}=\{\mathbf{z}_1, \cdots, \mathbf{z}_m, \cdots, \mathbf{z}_M\}, \mathbf{z}_m=\left(z_{m 1}, \cdots, z_{m n}, \cdots, z_{m_{N_m}}\right)\) 的后验概率分布 \(p(\mathbf{z} \mid \mathbf{w}, \alpha, \beta)\) 的样本计数, 模型的参数 \(\varphi\) 和 \(\theta\) 的估计值; 参数: 超参数 \(\alpha\) 和 \(\beta\), 话题个数 \(K\) 。

1. 设所有计数矩阵的元素 \(n_{m k}, n_{k v}\), 计数向量的元素 \(n_m, n_k\) 初值为 0 ;

2. 对所有文本 \(\mathbf{w}_m, m=1,2, \cdots, M\) 对第 \(m\) 个文本中的所有单词 \(w_{m n}, n=1,2, \cdots, N_m\)

1. 抽样话题 \(z_{m n}=z_k \sim \operatorname{Mult}\left(\frac{1}{K}\right)\);(对于文本m，其多项分布的参数为\(\frac{1}{K}\)，由\(\alpha\)生成，即\(\theta_m \sim Dir(\alpha)\)，\(\theta_m\)为长度为K的向量。)

增加文本-话题计数 \(n_{m k}=n_{m k}+1\), 增加文本-话题和计数 \(n_m=n_m+1\), 增加话题-单词计数 \(n_{k v}=n_{k v}+1\), 增加话题-单词和计数 \(n_k=n_k+1\);

（3）循环执行以下操作, 直到进入燃烧期 对所有文本 \(\mathbf{w}_m, m=1,2, \cdots, M\) 对第 \(m\) 个文本中的所有单词 \(w_{m n}, n=1,2, \cdots, N_m\)

1. 当前的单词 \(w_{m n}\) 是第 \(v\) 个单词, 话题指派 \(z_{m n}\) 是第 \(k\) 个话题; 减少计数 \(n_{m k}=n_{m k}-1, n_m=n_m-1, n_{k v}=n_{k v}-1, n_k=n_k-1\);

2. 按照满条件分布进行抽样

\[ p\left(z_i \mid \mathbf{z}_{-i}, \mathbf{w}, \alpha, \beta\right) \propto \frac{n_{k v}+\beta_v}{\sum_{v=1}^V\left(n_{k v}+\beta_v\right)} \cdot \frac{n_{m k}+\alpha_k}{\sum_{k=1}^K\left(n_{m k}+\alpha_k\right)} \]

得到新的第 \(k^{\prime}\) 个话题, 分配给 \(z_{m n}\);

3. 增加计数 \(n_{m k^{\prime}}=n_{m k^{\prime}}+1, n_m=n_m+1, n_{k^{\prime} v}=n_{k^{\prime} v}+1, n_{k^{\prime}}=n_{k^{\prime}}+1\);

4. 得到更新的两个计数矩阵 \(N_{K \times V}=\left[n_{k v}\right]\) 和 \(N_{M \times K}=\left[n_{m k}\right]\), 表示后验 概率分布 \(p(\mathbf{z} \mid \mathbf{w}, \alpha, \beta)\) 的样本计数;

4. 利用得到的样本计数, 计算模型参数

\[ \begin{aligned} \theta_{m k} &=\frac{n_{m k}+\alpha_k}{\sum_{k=1}^K\left(n_{m k}+\alpha_k\right)} \\\\ \varphi_{k v} &=\frac{n_{k v}+\beta_v}{\sum_{v=1}^V\left(n_{k v}+\beta_v\right)} \end{aligned} \]

训练与推断

有了LDA模型，我们的目标有两个：

• 估计模型中的参数\(\varphi_1, \cdots, \varphi_K\)和\(\theta_1, \cdots, \theta_M\);
• 对于新来的一篇doc，我们能够计算这篇文档的topic分布\(\theta_{new}\)。

有了吉布斯采样公式就可以基于语料训练LDA模型，并应用训练得到的模型对新的文档进行topic语义分析，训练的过程就是通过Gibbs Samping获取语料中的（z,w）样本，而模型中的所有参数可以基于采样的样本进行估计。

训练流程如下：

• 随机初始化：对语料中的每篇文档的每个词w，随机赋一个topic编号z。
• 重新扫描语料库，对每个词按照吉布斯采样公式重新采样它的topic，在语料中进行更新。
• 重复以上语料库的重新采样过程直到吉布斯采样收敛。
• 统计语料库的topic-word共现频率矩阵，就是LDA的模型

由这个矩阵我们可以计算每一个\(p(word\mid topic)\)概率，从而计算出模型参数\(\varphi_1, \cdots, \varphi_K\)，也可以计算另一个参数\(\theta_1, \cdots, \theta_M\)，只要在吉布斯抽样收敛后统计每篇文章的topic频率分布，就可以计算每一个\(p(topic\mid doc)\)概率，由于它是和训练语料的每篇文章相关的，对于我们理解新的文档毫无用处，所以一般没有必要保留这个概率。

如何对新的文档进行推断呢？其实和训练过程完全相似，对于新的文档，认为\(\varphi_{kt}\)是稳定不变的，是由训练语料得到的模型提供的。采样过程只估计该文档的topic分布\(\theta_{new}\)就好了。

推断过程如下：

• 随机初始化：对当前文档的每个词w，随机的赋一个topic编号z；
• 重新扫描当前文档，按照吉布斯抽样公式，对每个词w，重新采样它的topic；
• 重复以上过程直到吉布斯采样收敛
• 统计文档中的topic分布，该分布就是\(\theta_{new}\)

代码

实现了吉布斯推断的python代码：

"""

LDA implementation in Python

  

@author: Michael Zhang

"""

import matplotlib.pyplot as plt

import numpy as np

import scipy

  

class LDA(object):

    def __init__(self, tdm, T, alpha = 1., beta=1., iteration=100):

        """

        tdm: the copus, of (D, Num_words_in_corpus),

            the value of each entry is the counts of corresponding words in this the corresponding document.

            e.g.

            tdm[d, w] = number of word w appears in document d.

        T: the number of topics

        """

        self.tdm = tdm

        self.D, self.W = self.tdm.shape            

        self.alpha= alpha # count for expected value for hyper parameter alpha of theta, i.e. document-topic distribution.

        self.beta = beta # count for expected value for hyper parameter beta topic-word distribution.

        self.T = T

        self.iteration = iteration

        # z must take in (d,w,i) as input, corresponding to

        # topic indicator for i-th obserevation of word w in doc d

        self.z = {}

        self.topic_word_matrix = np.zeros((self.T, self.W)) # initialize the topic-word matrix.

        self.doc_topic_matrix = np.zeros((self.D, self.T)) # initialize the documnet-topic matrix.

        self.topic_counts = np.zeros(self.T) # initialize the topic counter for after sampling process, should be sum of value in self.topic_word_matrix

        self.doc_counts = np.zeros(self.D) # initialize the doc counter for after sampling process, should be sum of value in self.doc_topic_matrix

        self.log_likelihood = np.zeros(self.iteration) # store the value of log likelihood at each iteration

        self._init_matrix()

    # @pysnooper.snoop('init.log')    

    def _init_matrix(self):

        """

        for all words

        1. sample a topic randomly from T topics for each word

        2. increment topic word count, self.topic_word_matrix

        3. increment document topic count,  self.doc_topic_matrix

        4. update the topic indicator z.

        """

        for d in range(self.D):

            doc = scipy.sparse.coo_matrix(self.tdm[d])

            word_freq_topic = zip(doc.col, doc.data)

            for w, frequency in word_freq_topic: # (word, freq)

                for i in range(frequency):

                    ############ Finish the following initialization steps #############

                    # 1. sample a topic randomly from T topics for each word

                    topic = np.random.randint(self.T)

                    # 2. increment topic word count, self.topic_word_matrix

                    self.topic_word_matrix[topic, w] += 1

                    # 3. increment document topic count,  self.doc_topic_matrix

                    self.doc_topic_matrix[d, topic] += 1

                    # 4. update the topic indicator z.

                    self.z[(d, w, i)] = topic # d: document ID; w: word ID: i: instance ID，即在d中第几个w

  

        self.topic_counts = self.topic_word_matrix.sum(axis=1)

        self.doc_counts = self.doc_topic_matrix.sum(axis=1)

  

    # @pysnooper.snoop('fit.log')    

    def fit(self):

        for it in range(self.iteration):

            # iterate over all the documents

            for d in range(self.D):

            # iterate over all the words in d

                for w in self.tdm[d].indices:

                    # iterate over number of times observed word w in doc d

                    for i in range(self.tdm[d, w]):

                        # we apply the hidden-varible method of Gibbs sampler, the hidden variable is z[(d,w,i)]

                        self.doc_topic_matrix[d,self.z[(d,w,i)]] -= 1

                        self.doc_counts[d] -= 1

                        self.topic_word_matrix[self.z[(d,w,i)],w] -= 1

                        self.topic_counts[self.z[(d,w,i)]] -= 1

  

                        # estimation of phi and theta for the current corpus

                        phi_hat = (self.topic_word_matrix[:,w] + self.beta) / (self.topic_counts + self.beta * self.W)

                        theta_hat = (self.doc_topic_matrix[d,:] + self.alpha) / (self.doc_counts[d] + self.alpha * self.T)

  

                        # calculate the full conditional distribution

                        full_conditional = phi_hat * theta_hat

                        # normalize full_conditional such that it summation equals to 1.

                        full_conditional = full_conditional / full_conditional.sum()

                        # sample a topic for i-th obserevation of word w in doc d based on full_conditional

                        new_topic = np.random.multinomial(1, full_conditional).argmax()

                        # update z, doc_topic_matrix, doc_counts, topic_word_matrix, topic_counts here.

                        self.z[(d,w,i)] = new_topic

  

                        self.doc_topic_matrix[d,self.z[(d,w,i)]] += 1

                        self.topic_word_matrix[self.z[(d,w,i)],w] += 1

                        self.doc_counts[d] += 1

                        self.topic_counts[self.z[(d,w,i)]] += 1

                        ############################################################

  
  

            # Equation 2  log P(w|z)  for each iteration based on Equation [2]

            ## +++++++++ insert code below ++++++++++++++++++++++++###

            self.log_likelihood[it] = 0

            for k in range(self.T):

                for w in range(self.W):

                    self.log_likelihood[it] += self.topic_word_matrix[k,w] * np.log((self.topic_word_matrix[k,w] + self.beta) / (self.topic_counts[k] + self.beta * self.W))

            ############################################################

            print('Iteration %i\t LL: %.2f' % (it,self.log_likelihood[it]))

本质与使用条件

本质上说，主题模型根本上是实现文本数据的结构化，结构化的文档可以彼此比较和查询，实现传统的任务。 LDA主题模型本质上解决了两类问题： - 文档聚类 - 词汇聚类

主要价值在于： 1）文档的结构化，相比于传统的词袋模型达到了降维的效果 2）完成了文档的聚类和词汇的聚类，实现文本信息的抽象化分析，帮助分析者探索隐含的语义内容。

实践中数据要有以下性质才会有较好的结果：

1. 文档足够多
2. 文档足够长
3. 词汇特征够多
4. 词频足够大

总结

历时好几周，终于完结了主题模型，主要是概率论没有学好，跟着推导的过程过于痛苦，不过也算是稍微理解了一点LDA，复述一下：

LDA理解可以类比于PLSA，大体的思想都是根据文档生成主题分布，再根据主题分布和单词分布得到文档中的各个单词。不同的是LDA是贝叶斯派的思想，对于两种分布加入了狄利克雷先验概率。LDA的生成过程可以看成上帝掷骰子，从M个骰子中选取一个作为文本m的主题分布，从K个骰子中选取一个作为主题k的单词分布，（注意这里的多项分布的参数就是多项分布中的概率p，其服从狄利克雷分布，比如对于\(\theta_m\)，它其实就是文本m生成不同主题k的概率\(p(z\mid d_m)\)，是个K维的向量。对于\(\varphi_k\)，是由主题k生成不同单词v的概率\(p(w\mid z_k)\)，是个V维的向量。也就是根据狄利克雷分布采样得到的是一些概率，这些概率也是我们最终要求的参数，这些概率作为多项分布的参数再采样生成主题或者单词，还有就是\(p(z_k\mid d_m)\)与\(z_{mn}\)的理解，前者就是相当于\(\theta_{mk}\)，后者肯定是主题集合中的一个，不过是根据参数为\(\theta_m\)的多项分布在位置n采样得到的。这就是LDA的整个的理解，当然模型的求解是使用吉布斯抽样的方法，与上面写的步骤不同。写这些是便于理解）。

由主题分布可以对文本的每个位置赋值一个主题，再根据主题-单词分布可以生成整个文本。一切的一切都是和PLSA一样，求两个分布，以至于可以生成我们的文档。LDA也可以得到文档的主题分布，得到了主题分布和单词分布可以应用于各种任务当中。具体可以参考《LDA漫游指南》。

现在知道了LDA是怎么一回事了，但还是感觉模模糊糊的，感觉如“通俗理解LDA主题模型”这篇文章开头所说的那样陷入了LDA的细枝末节中，所以写了一些主题，加深自己的印象与理解，经过代码的洗礼，又理解深入了一些，但感觉还没有掌握的很好，可能需要消化消化，那就先告一段落了。以后常看看就行。 ## 参考

https://zhuanlan.zhihu.com/p/374924140 https://www.cnblogs.com/gasongjian/p/7631978.html